数式処理ソフト DERIVE(デライブ) de ドライブ
85.道中双六の問題(補筆2)
目次
(1)差分方程式から偏微分方程式の導出過程を再検証
偏微分方程式近似の問題点
∂(∂(f(x, t), t), x)をゼロと見なさず、∂(f(x, t), t, 2)をゼロと見なす近似に残る問題点
(2)平均日数を計算するためのDERIVEの関数
(3)平均日数と確率・最短日数のグラフ (2017/2/13 内容を修正、2017/2/14 グラフを一つ追加)
(1)差分方程式から偏微分方程式の導出過程を再検証
偏微分方程式近似の問題点
「第84回の『道中双六の問題(補筆1)』では、道中双六の問題について、主として、p=1/2 のケースについて、それまでの疑問点等を扱った。
元々の差分方程式は、以下のようじゃった。(『道中双六の問題(続)』)
f(0,0)=1
t<j → f(j,t)=0
j>c → f(j,t)=0
f(0,t)=(1-p)×f(1,t-1)
f(1,t)=f(0,t-1)
j<c-1 → f(j,t)=(1-p)×f(j+1,t-1)+p×f(j-1,t-1)
上記以外は、f(j,t)=p×f(j-1,t-1)」
図で見た方が分かりやすいじゃろう。
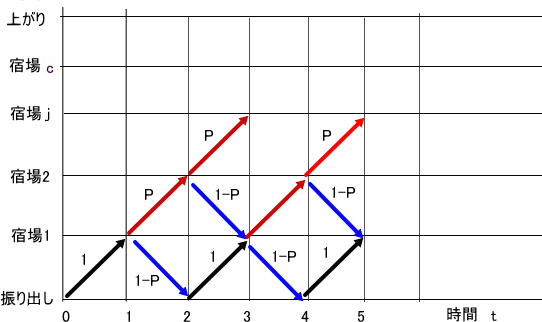
今回は、p が一般の場合について、扱うことにしよう」
 「それでは、まずは、今月のご挨拶の『道中双六の問題(続々)』(2016年4月)に記載した、pが1/2でない場合の検算から初めてみたいわね」
「それでは、まずは、今月のご挨拶の『道中双六の問題(続々)』(2016年4月)に記載した、pが1/2でない場合の検算から初めてみたいわね」
「ともちゃん、今回もよろしくお願いしますよ。
以下では、最短日数=宿場数+1=c、とする。
ともちゃんが、上で挙げてくれた2016年4月の今月のご挨拶に記載した方程式と境界条件などを再掲すると、
∂(f,t)=(1-2p)∂(f,x)+(1/2)∂(f,x,2)、
xの変域は、x=0~c、t は、0~∞ となる。
初期条件及び境界条件は、p=1/2 のケースと同じとする。
f(x,0)=δ(x)、
x=0で、∂(f,x)=0、
x=cで、f(x=c,t)=0、
と、こうなっておった。
ところが、先回りをして言ってしまうと、
p<>1/2 の場合は、この近似では、次の2つの問題が顕在化することが分かったのじゃ。
(1) 差分方程式の近似に用いた、∂(∂(f,x),t)を微少量と見なしてゼロと等置するのは、正しくない
(2) p=0 では、∂(f,t)=0、となって欲しいが、近似方程式では、そうならない。
まずは、(1)の問題点を、説明するんじゃが、差分方程式から、x 及び t の2次までのテイラー展開を利用した方程式をどの項も省略せずに示してご覧」
「えーと、こんな感じね。
3階以上の高階の導関数の項を省略して、
∂(f(x, t), t)=(2p - 1)∂(∂(f(x, t), t), x) + ∂(f(x, t), x, 2)/2 + (1 - 2p)∂(f(x, t), x) + ∂(f(x, t), t, 2)/2 、
赤字の部分が、おじぃさんが言うように、これまで、微少だろうと仮定して省略していた部分ね。
なお、特別な条件、p=1/2の場合は、
∂(f(x, t), t))=∂(f(x, t), x, 2)/2 + ∂(f(x, t), t, 2)/2、となって、∂(∂(f,x),t)、及び、∂(f,x)の項は、ゼロになってしまって消えてしまう。
この場合でも、∂(f(x, t), t, 2) は、残るけどね」
「ま、そういうことじゃ。
∂(f,x)の項は、p<>.1/2の場合に再び現れるので、それだけでよいと思っておったのじゃがな。
さて、p=1/2 の時も残った、∂(f(x, t), t, 2)、や、p<>1/2の場合には、ゼロとならない ∂(∂(f(x,
t), t), x) の項は、微少であるという仮定の元にこれまで無視してきたんじゃった。
その近似による偏微分方程式に基づいて、p=1/2 の条件の下で平均日数を計算してみると、平均日数=c^2、であることを説明できた。
これは、一部のcだけではあるが、差分方程式から直接、DERIVE、及び、Excelで計算した結果と合致しておった。
しかし、p<>1/2の際は、従来近似の偏微分方程式を基にしたのでは、問屋が卸さない、ということがわかった。
下の図を見て欲しい。
Excel表でc=6、(宿場数が5)の場合の、∂(f,x)、∂(f,t)、∂(f,t,2)、∂(∂(f,x),t)、の4つの絶対値を示したものじゃ。
上から、この順になっておる。(図は、p=1/2の場合)

明るい赤い色で塗りつぶしたセルは、絶対値が0.1 より大きいものじゃ。
横軸が時間 t、縦軸がx、(xは、下から上に0~6まで)。
これを見ると、∂(f,t,2)は、t=0付近を除くと、ほぼ、微少である見なすことができる。
しかし、∂(∂(f,x),t)は、x=0付近を中心にt=33付近まで、0.1を超えている」
「なるほど。
p=1/2 の場合、∂(f,t,2)を無視したのは、正しいようね。
じゃ、pが1/2でない場合も、図示してみるよ。
まずは、pが1/2より大きい p=0.7の場合。

やはり、上から順に、∂(f,x)、∂(f,t)、∂(f,t,2)、∂(∂(f,x),t)、の絶対値ね。
∂(f,t,2)は、微少で、∂(∂(f,x),t)は、p=1/2の時よりも、絶対値が0.1を超えるtの範囲は狭まってはいる。
次に、p<1/2の例として、p=0.3 の場合。

上から順に、∂(f,x)、∂(f,t)、∂(f,t,2)、∂(∂(f,x),t)、の絶対値ね。
∂(f,t,2)は、微少で、∂(∂(f,x),t)は、p=1/2の時よりも、絶対値が0.1を超えるtの範囲が大幅に広がる。
実際、∂(∂(f,x),t)は、x=0の付近を中心に、t=0~635まで、連続して、絶対値が0.1を超えていたわ」
「これで分かったように、そもそも、∂(∂(f,x),t)を微少量として、無視するのは、許されなかったのじゃな。
しかし、p=1/2の場合に、それが影響しなかったのは、その項の係数、(2p-1)が、まさに、p=1/2の時、ゼロとなっていたからじゃ。
これが、(1)で挙げた問題点の中身だな」
「じゃ、∂(f,t,2)のみを微少量としてゼロと置き、
∂(f(x, t), t)=(2p - 1)∂(∂(f(x, t), t), x) + ∂(f(x, t), x, 2)/2 + (1 - 2p)∂(f(x, t), x) 、と近似すれば、いいのかしら?」
「そのようじゃな。
各項を省略しない形の方程式は、
∂(f(x, t), x, 2)/2 +(2p - 1)∂(∂(f(x, t), t), x)+∂(f(x, t), t, 2)/2 +(1 - 2p)∂(f(x, t), x) -∂(f(x, t), t)=0、となるが、
ここで、2階の偏微分方程式の一般論に従い、判別式、B^2-4AC、を作ってみる。(このあたりの詳細は、今回は省略)
∂(f(x, t), x, 2)の係数をA、∂(∂(f(x, t), t), x)の係数がB、∂(f(x, t), t, 2)の係数がC じゃ。
判別式=(2p - 1)^2-4×1/2×1/2=(2p - 1)^2-1=4p(p-1)、となり、負またはゼロとなる。
判別式がゼロとなるのは、p=0、及び p=1 のときで、『放物型』の偏微分方程式となる。
放物型の方程式は、熱伝導の場合などに現れることには、前に触れたな。
それ以外のpの場合は、負となり、『楕円型』の偏微分方程式に分類されるのじゃ。
楕円型は、通常は、『境界値問題』に現れて、周囲の境界における関数の値または導関数の値が定まっているときに内部の関数の値を求める場合に現れる方程式なのだ。
静電場の問題に現れるポアソンの方程式などが例じゃな。
なお、ともちゃんの提案の通り、∂(f(x, t), t, 2) を略してしまうと、判別式は、(2p-1)^2、となり、この値は、ゼロまたは正となる。
ゼロとなるのは、p=1/2、の場合で、『放物型』、
p<>1/2では、正で、これは、『双曲型』となり、双曲型の方程式は、水の波や太鼓の振動などに現れる。
ちなみに、従来近似の偏微分方程式は、A=1/2、B=0、C=0、の場合となるので、判別式 B^2-4AC=0、となり、『放物型』に入る」
「結構、条件によって、タイプが違ってくるのね。
そのあたりを表に整理してみたよ」
| |
∂(∂(f(x, t), t), x) |
| ゼロと見なさない |
ゼロと見なす |
| ∂(f(x, t), t, 2) |
∂(f(x, t), t, 2) |
| ゼロと見なさない |
ゼロと見なす |
ゼロと見なさない |
ゼロと見なす |
| p=0 |
放物型 |
放物型 |
楕円型 |
放物型 |
| 0<p<1/2 |
楕円型 |
双曲型 |
楕円型 |
放物型 |
| p=1/2 |
楕円型 |
放物型 |
楕円型 |
放物型 |
| 1/2<p<1 |
楕円型 |
双曲型 |
楕円型 |
放物型 |
| p=1 |
放物型 |
放物型 |
楕円型 |
放物型 |
「なるほど、これは、分かりやすい表じゃ。
方程式の型から見れば、わしらが考えたいのは、緑または水色のところじゃな。
一方、宿場数5の場合の実例を元にすると、一般には、∂(∂(f(x, t), t), x)をゼロとは、見なせないことは、先に触れた。
要点を繰り返すと、
p=1/2の場合は、その係数がゼロとなるため、∂(f(x, t), t, 2) をゼロと見なせば、都合よく、放物型となっていたのじゃな。
このときの方程式は、∂(f(x, t), t)=∂(f(x, t), x, 2)/2 となって、∂(∂(f(x, t), t), x)、及び、∂(f(x, t), t, 2)をゼロと見なした場合の式と一致する。
このため、実際は、∂(∂(f(x, t), t), x)をゼロと見なせないにもかかわらず、p=1/2 では、問題点があらわにならなかった理由が分かったじゃろう。
となれば、p<>1/2 のケースを考えるとき、
∂(∂(f(x, t), t), x)をゼロと見なさず、∂(f(x, t), t, 2)をゼロとは見なす近似によればよいと思うじゃろう。
だが、それは、必ずしも、十分条件ではないとも思われるのじゃ。
それが、(2)の問題なのだ。
次節で考えてみよう」
目次へ戻る
∂(∂(f(x, t), t), x)をゼロと見なさず、∂(f(x, t), t, 2)をゼロと見なす近似に残る問題点
「それが、p=0 では、∂(f,t)=0、となって欲しいんじゃが、近似方程式では、そうならない、という問題じゃ
∂(∂(f(x, t), t), x)をゼロと見なさず、∂(f(x, t), t, 2)をゼロと見なす近似によれば、方程式は、次のものとなるじゃろう。
∂(f(x, t), x, 2)/2 +(2p - 1)∂(∂(f(x, t), t), x)+(1 - 2p)∂(f(x, t), x) -∂(f(x, t), t)=0、
上式において、p=0とすると、
∂(f(x, t), x, 2)/2 -∂(∂(f(x, t), t), x)+∂(f(x, t), x) -∂(f(x, t), t)=0、となるんじゃが、
もし、p=0であれば、f(x,t)は、tによらないはずなので、仮に、それをg(x)と置いてみると、g ''+2g '=0、を満たす特別なg(x)のみが許されることになる。
しかし、初期の関数形は、自由に決められるので、これは、おかしい。
一方、p=1 と置いたときは、
∂(f(x, t), x, 2)/2 +∂(∂(f(x, t), t), x)-∂(f(x, t), x) -∂(f(x, t), t)=0、となる。
このとき、もし、f(x,t)の初期関数形をg(x)として、t=tの時の解を g(x-t)と仮定すれば、このg(x-t)は、上の方程式の解になっていることが分かる」
 「p=0、は、方程式を解くまでもなく、初期の関数形が変わらないので、例外なんだけど。
「p=0、は、方程式を解くまでもなく、初期の関数形が変わらないので、例外なんだけど。
でも、p≒0の場合は、確かに近似上の問題があるかも知れないわね。
だけど、極端にゼロに近いpを除けば、
∂(f(x, t), x, 2)/2 +(2p - 1)∂(∂(f(x, t), t), x)+(1 - 2p)∂(f(x, t), x) -∂(f(x, t), t)=0、
を解くことによって、p<>1/2の場合の姿を、大まかには、とらえられんじゃないかしら」
「確かにな。
しかし、p<>1/2の場合は、『双曲型』の偏微分方程式なので、準備のため、次回に回すことにしよう。
次節では、Excel では、十分な精度で平均日数を計算できなかったケースも扱えるようなDERIVEの関数を定義してみよう」
目次へ戻る
(2)平均日数を計算するためのDERIVEの関数
 「『道中双六の問題(続)』で定義した再帰呼び出しを使った関数は、宿場数が多くなると、時間がかかってしまっていたわね」
「『道中双六の問題(続)』で定義した再帰呼び出しを使った関数は、宿場数が多くなると、時間がかかってしまっていたわね」
「そうじゃったのう。
そこで、2つのベクトルと3つの関数を定義してみた。
ベクトル u、v の添え字 i は、1~c+3、(1は、振り出し、c+1が上がり、c=宿場数+1)、を動くものとする。
u=f(i,t-1)、v=f(i,t)、ただし、時間は、離散的とし、1~、と考える。
なお、i=1~c+1、の間は、t=tの時点のその位置における確率を格納する。
ただし、便宜上、i=c+2 には、平均日数を、i=c+3 には、確率の和を、それぞれ格納することにした。
しかし、いつものことながら、DERIVEでの『繰り返し処理』は、迷うのう」
「繰り返しは、基本的には、Iterate(Iterates)関数でしょ。
たとえば、nの階乗は、、
(ITERATE([w↓1·w↓2, w↓2 + 1], w, [1, 1], n))↓1、と書けば、いいのよ。
ここで、作業用のベクトル wのw↓1は、階乗自身、w↓2は、変数 k を格納した置くためのもの。
上の関数は、nが5の場合、
最初に、第3引数の初期ベクトル[1,1]が第1引数のベクトルに代入される。
この計算では、w=[1,1]、となる。
2回目の計算で、w=[1,2]、(w↓1が1の階乗)
3回目の計算で、w=[2,3]、(同様に、2の階乗)
・・・と、なって、6回目の計算で、
w=[120,6]、となり、このwの1列は、5の階乗なので、それを取り出すのが、Iterate関数にかかっている、↓1、なの。
つまり、Iterate関数の計算は、第4引数の数字+1回行われるというところが間違えやすいのよ」
「ともちゃんが書いてくれた例で、Iterate 関数をIterates 関数に変えると、下図のように、計算過程が分かりやすいじゃろう。

Iterates 関数の処理内容は、Iterate 関数と同じじゃ。
だが、結果をベクトルとして返す関数なので、上の図のように、6回の計算が行われて、6回目で求める5!が計算されていることが分かる。
※上の説明は、Iterate関数の説明用なので、DERIVEでは、階乗は、n ! で計算すればよい。
さて、平均日数を計算する問題に戻るぞ。
大まかな考えは、u からv を求める。ここで、最初の繰り返し処理は、i=1~c+1、が必要じゃ。
(実際は、先に書いたように、c+2列目、c+3列目を平均日数、確率の和の計算用として利用するので、繰り返しは、i=1~c+3となる)
ここで、困るのは、i によって、u を基に v の要素を求める計算式が異なる点じゃ。
そこで、関数 h(i,c,p)を定義して、v↓i =h(i,c,p)、と計算させることにした。

上の図は、関数 h を作る際の手助けをしてくれるじゃろう。
頭の中だけで考えて、むやみに作ろうとすると、(わしのように)苦労する。
例として、c=2~5、を挙げてみた。
この図を見ると、i=1(灰色の背景)では、常に、(1-p)u↓2、であることが分かる。
なぜならば、振り出しに入ってくる矢印は、青矢印(確率=1-p)のみなのでな。
これから、h(1,c,p)=(1-p)u↓2、とすればよい。
ところが、i=2では、cにより2つの状態がある。
c=2、では、黒矢印(確率1)のみが入ってくるので、h(2,2,p)=u↓2
c>2 では、黒矢印と青矢印の2つなので、h(2,c,p)=(1-p)u↓3+u↓1、
同様に、上がり一つ前の宿場(i=c)も、c=2のときとc>2では、異なる。
ただし、i=2のケースは、すでに触れていて、h(2,2,p)=u↓2、
一方、c>2では、赤い矢印(確率p)のみが入ってくるので、h(i,c,p)=p u↓(i-1)、
上がり(i=c+1)は、共通で、赤い矢印のみなので、h(c+1,c,p)=p u↓c、
最後に中間の場合、青と赤の矢印が入ってくるので、h(i,c,p)=(1-p)u↓(i+1)+p u↓(i-1)、となる。
以上を考慮して、作ったのが、下の図に示す関数、h じゃ。

なお、i がc+1を超える場合、具体的には、i=c+2、は、平均日数、i=c+3は、確率の和の計算用なので、u の値をそのまま返すことにした」
「なるほど。
これを呼び出して、u からvを計算させるときは、どうするのかしら?」
「うん。
Basic言語などでは、Iterate関数は、無いので、基本的には、For ループか、または、Do While 条件式~、のようなループ処理で、あまり迷いはないのじゃがな。
ここは、配列を作成する関数、Vector 関数を使うのが簡単じゃ。

g2関数では、h によりuを元に i=1~c+3まで計算して作った配列をvに代入する。
v ≔ VECTOR(h(i, c, p), i, 1, c + 3)、がその処理だ。
それに続く2行は、
i=c+2、の方が平均日数を計算して、足し込む。
v↓(c + 2) ≔ v↓(c + 2) + k_·v↓(c + 1)
また、i=c+3は、確率の和を足し込むための計算じゃ。
v↓(c + 3) ≔ v↓(c + 3) + v↓(c + 1)、
最後に、こうしてできあがった、v を新しいuに代入するのだな」
「g2の第3引数のk_ は、時間を与えるための引数ね」
「そうじゃ。
このg2は、メイン関数であるg1(c,p,n)から、次のように呼び出して使う。

メイン関数のg1のなかで、
最初の3行は、作業用ベクトルである uとvを初期化する命令じゃ。(u、vは、100次元としている)
3行目の、u↓1:=1、が初期の旅人(の密度)だな。
ここでは、繰り返し処理のために、Iterate 関数を使った。
最初は、g2と同様に、Vector 関数を使った。
しかし、cが小さいときは、よいんじゃが、c=54ともなると、メモリーを食ってメモリーオーバーとなってしまう。
それで、Iterate関数を使ったのじゃ」
「Iterate関数で、
ITERATE([g2(c, p, z_↓2), z_↓2 + 1], z_, [0, 1], n)、の z_は、仮の配列ね。
z_の2列目の要素を繰返し回数のカウンターとして使っていると言うことになるわ。
そして、そのカウンターは、時間でもあるので、g2関数のk_ に引き渡す。
実際に計算させてみたよ。
g1(2,p,10)とすれば、
[p·(p^4 - 5·p^3 + 10·p^2 - 10·p + 5), 2·p·(5·p^4 - 24·p^3 + 45·p^2 - 40·p + 15)]、が戻る。
第1列が確率の和、第2列が平均日数、(g1の関数の最後で、[u↓(c + 3), u↓(c + 2)]、として順番を逆に表示させていることに注意。
c=2の時、2m 日、(m=1~)で上がる確率は、f(2m)=p×(1-p)^(m-1)、なので、
確率の和は、Σ(m=1~5)f(2m)=p·(p^4 - 3·p^3 + 4·p^2 - 2·p + 1)、
また、平均日数は、Σ(m=1~5)2m×f(2m)=2·p·(5·p^4 - 16·p^3 + 21·p^2 - 12·p + 3)、
注意しないといけないのは、厳密解は、2m 日ごとに上がりとなる確率なので、平均日数を計算するときに、
Σ2m×f(2m)、とする必要があることね。(cが一般の場合は、m=1~、として、2(m-1)+c 日ごとに上がる)
逆に、DERIVEのg1関数では、厳密解で5個利用しているとき、nは、その2倍の10回とするのを忘れないように。
とは言っても、今回は、n を大きくとり、確率の和が十分に1に近い場合を計算するので、そんなに神経を使う必要は無い」
「そこで、次節では、平均日数を異なるcやpを基に計算し、その結果により、平均日数を c とp の関数として近似することを考えてみよう」
目次へ戻る
(3)平均日数と確率、最短日数のグラフ
 「最短日数 c=2、3、4、の場合について、確率 p=0.1~1まで、0.02 刻みで変化させて、グラフを描いてみた。
「最短日数 c=2、3、4、の場合について、確率 p=0.1~1まで、0.02 刻みで変化させて、グラフを描いてみた。
ただし、縦軸の平均日数は、自然対数値 Ln(平均日数)を表している。

横軸は、確率 pの値そのもの。
c=2と3については、g1関数の繰返し回数を1000回とした。(確率の和は、0.99以上)
c=4については、0.1から0.2までは、1万回、それ以降は、3000回とした」
「わしは、平均日数の近似曲線を工夫してみた。
今回、c=2の厳密解 LN(2/p)、及び、c=3の厳密解 LN(1+2/p^2)、から、
Ln(平均日数)≒LN(c)·((c - 2)·LN((p^2 + 2)/p^2)/LN(3) + (3 - c)·LN(1/p)/LN(2)
- c + 3)、と置いた。
これだけ見ると、c=2~4の範囲では、ほぼ合っているようだな」
「なるほど。
じゃ、c=5の場合をやってみるよ。
p=0.1で、平均日数≒1.659973461·10^4、
確率の和=0.9999941578, (繰返し回数=20万回)
p=0.2では、平均日数≒900.8437887、(繰返し回数=1万回)
確率の和=0.9999856637,
p=0.2~0.5までは、繰返し回数 1万回、
p=0.5~1までは、繰返し回数 1000回として計算。

この2つめのグラフを見ると、c=5の場合が分かりやすいけど、近似曲線と計算値の乖離が、やや進んできているなと感じるわね。
けれど、いきなり、c=54の東海道五十三次の場合に挑戦してみたよ。
Ln(平均日数)≒(LN(c)·((c - 2)·LN((p^2 + 2)/p^2)/LN(3) + (3 - c)·LN(1/p)/LN(2) - c + 3))
ここで、c=54と代入。

しかし、上のグラフで分かるように、単調減少ではなくて、p=0.8付近でやや下にくぼんでしまっている。
なお、この式を基にp=0.1の場合に外挿してみると、Ln(平均日数)≒122、となる。
よって、平均日数の実数は、1×10^53 程度と予想できるのではないかしら」
「わしは、p を固定して、c を動かして計算してみた。

上のグラフのように、p=0.1~1、c=2~25、の間で変化させて、平均日数を計算した。
なお、p=0.1 のように小さくなると、途方もなく、計算時間がかかってしまうので、c=5~10ぐらいに抑えている。
前の近似式からは、
LN(平均日数)≒(LN(c)·((c - 2)·LN((p^2 + 2)/p^2)/LN(3) + (3 - c)·LN(1/p)/LN(2)
- c + 3))、となるが、
これを基礎にすると、下のグラフのようになる。

p=0.1~0.4のあたりは、もっともらしいが、p>0.5では、c=45付近で、減少に転じているのは、おかしい。
とはいえ、大まかには、様子を再現していると言えるじゃろう。
考えてみると、c=2とc=3における2つの厳密解だけを基にした割には、意外に全体的な傾向を見て取れるようにも思う。
LN(平均日数)≒LN(c)×(α+βc)、のαとβのpとの関係を、参考として、下図に示す。

ドットで表したものが計算値じゃ。
実線は、c=2、c=3での厳密解を基にして、推定した上掲の近似式によるものだ。
傾向は、合っているが、少しずれがある。
これ以上細かなことは、p<>1/2の際の近似偏微分方程式を解いてから考えることにしよう」
目次へ戻る
最終更新日 2017/2/24




 「それでは、まずは、今月のご挨拶の『道中双六の問題(続々)』(2016年4月)に記載した、pが1/2でない場合の検算から初めてみたいわね」
「それでは、まずは、今月のご挨拶の『道中双六の問題(続々)』(2016年4月)に記載した、pが1/2でない場合の検算から初めてみたいわね」
