数式処理ソフト　DERIVE（デライブ） de ドライブ

９２．マルコフ過程（5）（非対称型道中双六：固有方程式の一般形）

目次

（1）　概要
（2）　ベクトルと行列を使った漸化式の高速化
（3）　c＝54の固有方程式の解（根）
（4）　固有方程式の一般形
　※　c＝宿場数+1　

（1）概要

第91回『マルコフ過程（4）（非対称型道中双六：固有方程式の漸化式）』において、推移確率行列の固有方程式を求めました。
　※　推移確率行列や状態ベクトルでは、「上がり」を除いて考えています。

　

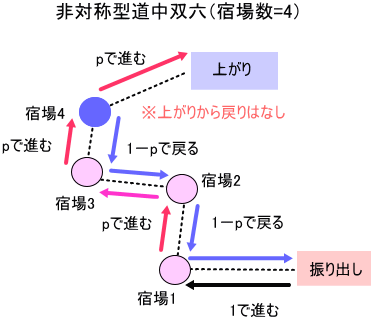
　c ＝宿場数+1として、具体的な固有方程式 Φ(c)は、
　変数をλ、確率 p、補助的な関数、f と g を使って、
　Φ(c＝奇数)＝－λ×f(c－1)－(1－p)×g(c－2)、
　Φ(c＝偶数)＝－λ×g(c－1)－(1－p)×f(c－2)、となりました。
　ここで、補助的な関数、f と g は、
　n を0以上の偶数として、f(n+2)＝－λ×g(n+1)－p(1－p)×f(n)、ただし、f(0)＝１、
　n を1以上の奇数として、g(n+2)＝－λ×f(n+1)－p(1－p)×g(n)、ただし、g(1)＝－λ、青字個所を2018/7/10修正
　で定義される（帰納的）再帰関数です。
　計算時間は、cが20程度までが1秒以下、c＝25で約6秒、c＝30で約70秒程度でした。
　cが増えると急に時間がかかる理由は、f (n + 2)がg(n + 1)とf(n) に、g(n + 3)がf(n + 2)とg(n + 1) にという相互に依存する再帰計算のためだと思われます。
　そこで、今回、計算時間の高速化を追求した結果、以下の3つの結果が得られました。

　（1）　2次元のベクトルと行列を使う計算法により、固有方程式を求める時間を大幅に短縮しました。
　　たとえば、c＝30では、約0.02秒、懸案の c＝54でも、約0.06秒程度と高速化されています。

　（2）　c＝54の場合の固有方程式は、54次方程式となります。
　　第91回に述べたように、変数の2乗を新変数と置き換えることにより、54次方程式は、27次方程式に変換できます。
　　この27次方程式の一般解は、求められませんので、特定の p、ここでは、p＝1/2 について、数値計算を行い、27個の単根を求めました。
　　また、その際の方程式のグラフを描画しました。

　（3）　第88回の推移確率行列の対角化の方法を（1）の計算に利用できることが分かり、任意の c に対する固有方程式の一般形を書き下ろしました。
　　この一般形により、第91回で証明した事柄、cが偶数では、方程式がλ^2の多項式、奇数では、λ×（λ^2の多項式）、をあらためて確認しました。
　　なお、一般形を使った計算時間は、c＝54では、ベクトルと行列による計算法と同程度でした。　
　目次へ戻る

（2）ベクトルと行列を使った漸化式の高速化

「お、ともちゃん。
　今回は、ともちゃん先生の行列式の講義じゃなかったのかいな？」

「それがね。
　第91回の固有方程式の漸化式を高速化するという宿題に足を取られてしまって。
　まず、宿題を片付けようと思ったのよ。
　なので、行列式は、次回に回させてもらうわ」

「ほう、爽快、いや、そうかいな。
　では、その前に、わしから、用語の補足をしておこう。
　前回、『固有方程式の漸化式』と書いたんじゃが、正確には、少し事情が違う。
　c ＝宿場数+1として、固有方程式を、Φ(c) 、変数をλ、確率を p と書いたとき、
　Φ(c＝奇数)＝－λ×f(c－1)－(1－p)×g(c－2)、
　Φ(c＝偶数)＝－λ×g(c－1)－(1－p)×f(c－2)、
　となり、これを見ると、Φは、f と g の一次結合じゃからの。

　普通、漸化式というと、みなさんは、
　Φ(c)＝○×Φ(c－1) + ○×Φ(c－2)+・・、のようなものを思い浮かべるじゃろう。
　では、漸化式が、どこにあるかと問われれば、それは、f と g なんじゃ。
　すなわち、
　n を0以上の偶数として、f(n+2)＝－λ×g(n+1)－p(1－p)×f(n)、ただし、f(0)＝１、
　n を1以上の奇数として、g(n+2)＝－λ×f(n+1)－p(1－p)×g(n)、ただし、g(1)＝－λ、青字個所を2018/7/10修正
　と定義される」

「う～ん。
　確かに、そうなんだけどね。
　ま、ややこしいので、パス。
　当面、固有方程式の漸化式、のような言い方でいいんじゃない。

　さてと、おじぃさんが説明してくれたように、本当の漸化式は、f と g なのね。
　フィボナッチ数列のところで、再帰関数の計算に時間がかかる場合、ベクトルを使って高速化する方法が出てきたでしょ。
　※第62回『再帰関数（1）（等差・等比数列、フィボナッチ数列、繰り返し処理）』
　でも、今回は、f と g という2つの関数の組み合わせなのよね。
　最初は、f と g を別々にして、
　u＝［f(0)，f(2)］、v＝［g(1)，g(3)］のような2組のベクトルで f と g を個別に求めようと考えてみたんだけど、思うようにいかないのね」

「フィボナッチ数列とは、懐かしいのう。2013年の頃の話じゃ。
　そこで、どうやったのじゃな」

「f と g を1つに組み合わせてみたの。
　以下、f(0)、g(1) などを f1 などと略記する場合があるわ。
　
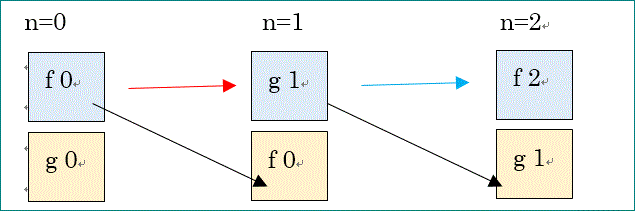
　上の図で、漸化式だから、nがc に相当するけど、nを時間のように考えた方が分かりやすい。
　まず、n＝0 の状態が初期状態なんだけど、
　実は、g (0) は、前回は、定義されていなかったのね。
　だけど、すぐ下に書いているように、g(0)を定義した方が簡素化されることが分かったの。

　n＝0の状態から、n＝1の段階に進むための計算として、
　上の図の赤い矢印は、g(1)＝－λ·f (0)－p·(1－p)·g (0) であり、
　f(0)＝1なので、 前回のgの初期値 g(1)＝－λを満たすためには、（新しい初期値として）g (0)＝0、とすべきことが分かった。
　黒い矢印は、n＝0 の第1要素をn＝1の第2要素にコピーするだけの働きを表す。

　次に、n＝1の状態から、n＝2の状態に進むための計算を考える。
　青い矢印は、f (2)＝－λ·g (1)－p·(1－p)·f (0)、
　黒い矢印は、n＝1 の第1要素をn＝2の第2要素にコピーするだけの働きを表す。

　以上の事柄を数学的に整理するために、2次元の縦ベクトル V を考えて、
　上の図から初期ベクトルをV(0)と書けば、
　
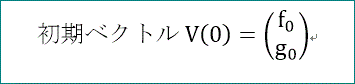
　である。

　また、m＝0～、の整数としたとき、
　n＝2m+1 のベクトルは、
　
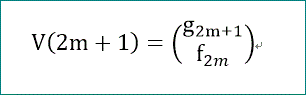
　n＝2m+2 のベクトルは、
　
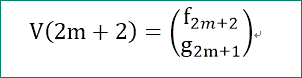
　となることが見て取れるわ」

「なるほど。
　再帰関数の高速化のために、ベクトルを使うのは、常套手段じゃが、ともちゃんが定義したベクトル Vでは、
　第1、第2要素が f 、g のいずれと定まってなくて、n が一つ進む毎に、第1要素と第2要素との間で、f と g が交互に入れ替わるのじゃな。
　いや、目の付け所がよかったのう」

「へへ、でしょ。
　具体的には、
　赤い矢印の計算は、g (2m+3)＝－λ·f (2m+2)－p·(1－p)·g (2m+1)、なんだけど、
　ベクトル V を使えば、
　V(2m+3)↓1＝－λ V(2m+2)↓1－p(1－p) V(2m+2)↓2、であることが分かる。
　ここで、下向きの矢印の後の数字は、ベクトルの要素番号を示す。

　一方、青い矢印の計算は、f (2m+2)＝－λ·g (2m+1)－p·(1－p)·f (2m)、だけど、
　ベクトルVを使えば、
　V(2m+2)↓1＝－λ V(2m+1)↓1－p(1－p) V(2m+1)↓2、であることが分かる。

　そこで、注目すべき点は、
　V(2m+3)↓1 の計算式において、m → m－1 と置き換えても、
　V(2m+2)↓1の計算式と同一になることよ。
　よって、
　V(n+1)↓1＝－λ V(n)↓1－p(1－p) V(n)↓2
　と書けることが分かるでしょ。
　また、黒い矢印は、
　V(n+1)↓2＝V(n)↓1、と表すことができる。

　ここで、マルコフ過程にならって、推移確率行列に相当する行列として、2次の行列Aを、
　
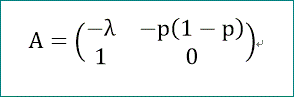
　と定義すれば、ベクトルVを状態ベクトルのように考えて、
　V(n+1)＝A V(n)、と表すことができる。
　これから、直ちに、
　V(n)＝A^n V(0)、が導かれる。
　右辺のV(0)は、前述のように
　
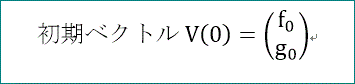
　となっている」

「いや、これは、驚いたのう。
　ただ、V(n) は、nの偶奇により、どっちかが、f か g かを分けて考えないとΦが求められんじゃろう」

「そのとおり。
　V(n)は、
　
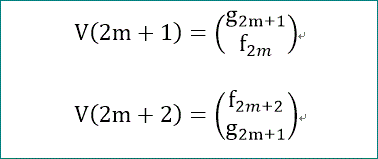
　となるので、
　nが奇数の場合、n＝2m+1から、V(2m+1)↓1 が g (2m+1) 、V(2m+1)↓2 が f (2m)、
　nが偶数の場合、n＝2m+2から、V(2m+2)↓1 が f (2m+2) 、V(n)↓2 が g (2m+1)、
　であることが分かる。

　さて、上の結果を踏まえて、V(n)からΦ(c) を計算する方法を考えるわよ。
　n が奇数の場合は、
　Φ(n)＝－λ·f( n－1)－(1－p)·g( n－2)
　から、n＝2m+3と置けば、
　Φ(2m+3)＝－λ·f( 2m+2)－(1－p)·g(2m+1)
　と書けるので、
　Φ(2m+3)＝［－λ，－(1－p)］’・V(2m+2)、となる。
　ここで、右辺第1項は、横ベクトル ［－λ，－(1－p)］の転置ベクトル、
　右辺の「・」は、2つのベクトルの内積の計算を表す。

　一方、n が偶数の場合は、
　Φ(n)＝－λ·g(n－1)－(1－p)·f(n－2)
　から、n＝2m+2と置けば、
　Φ(2m+2)＝－λ·g( 2m+1)－(1－p)·f( 2m)
　と書けるので、
　Φ(2m+2)＝［－λ，－(1－p)］’・V(2m+1)、となる。

　ここで、分かったと思うけど、
　cの偶奇により、式を分ける必要がなくなり、
　c を2以上の整数として、
　Φ(c)＝［－λ，－(1－p)］’・V(c－1)、
　と計算できる。

　右辺のV(c－1)は、V(c－1)＝A^(c－1) V(0)、
　により計算できるので、
　Φ(c)＝［－λ，－(1－p)］’・A^(c－1) V(0)、とまとめられる。
　さらに、V(0)＝［1，0］‘ を使えば、
　Φ(c)＝［－λ，－(1－p)］’・A^(c－1) ［1，0］‘、
　ここで、Aは、2次の行列で、
　
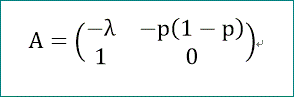
　である。
　今までもそうだけど、A は、推移確率行列ではないので注意してね。
　たとえば、c＝2では、
　Φ(2)＝［－λ，－(1－p)］’・A^(1) ［1，0］‘
＝［－λ，－(1－p)］’・［－λ，1］’
＝λ^2－(1－p)、となる」

「c＝2の計算は、分かったが、任意のc に関するDERIVEの関数は、どうなったのかな？」

「そうね。
　ここで、DERIVEの関数として、Φの代わりとなる新しいΦnew を作成する。
　Φnew(x_，n_)、ここで、引数として、変数x_ 、n_ を使用して、
　n_のエラーチェックを別にすれば、
　Φnew(x_, n_ )≔
　　　　　　　PROG(
　　　　　　　　　v1_ ≔ [－x_, － (1 － p)]`,
　　　　　　　　　v2_ ≔ [1, 0]`,
　　　　　　　　　A_ ≔ [－x_, － p·(1 － p); 1, 0],
　　　　　　　　　v1_ ⋅ A_^(n_ － 1)·v2_
　　　　　　　)
　となるでしょう。
　ここで、v1_ は、作業用ベクトル、v2_ は、初期ベクトル、A_ は、2次の行列である。
　上に、n_のチェックのために、Φ にならって、以下の2つの命令を追加する。
　IF(INTEGER?(n_) ＝ false, RETURN "Not Integer"),
　IF(n_ < 2, RETURN "Number < 2"),

　そうすれば、
　Φnew(x_, n_) ≔
　　　　PROG(
　　　　　IF(INTEGER?(n_) ＝ false, RETURN "Not Integer"),
　　　　　IF(n_ < 2, RETURN "Number< 2"),
　　　　　v1_ ≔ [－x_, p － 1]`,
　　　　　v2_ ≔ [1, 0]`,
　　　　　A_ ≔ [－x_, p·(p － 1); 1, 0],
　　　　　v1_ ・ A_^(n_ － 1)·v2_
　　　　　)
　高速化ができているかどうかのテストとして、
　高速化前は、cが30では、約70秒程度を必要とした。
　Φnewでは、0.016秒となり、ほぼ、瞬時と言って良いでしょう」

「よっしゃ。
　では、c＝54の場合を計算してみよう。
　Φnew(z，54)＝
(z^54 + z^52·(52·p^2 － 51·p － 1) + 51·p·z^50·(p － 1)^2·(25·p + 1) + 1225·p^2·z^48·(p － 1)^3·(16·p + 1) + 9212·p^3·z^46·(p － 1)^4·(23·p + 2) + 38916·p^4·z^44·(p － 1)^5·(44·p + 5) + 1533939·p^5·z^42·(p － 1)^6·(7·p + 1) + 1338117·p^6·z^40·(p － 1)^7·(40·p + 7) + 11344905·p^7·z^38·(p － 1)^8·(19·p + 4) + 177232627·p^8·z^36·(p － 1)^9·(4·p + 1) + 112784399·p^9·z^34·(p － 1)^10·(17·p + 5) + 133767543·p^10·z^32·(p － 1)^11·(32·p + 11) + 1579730984·p^11·z^30·(p － 1)^12·(5·p + 2) + 429757960·p^12·z^28·(p － 1)^13·(28·p + 13) + 1160346492·p^13·z^26·(p － 1)^14·(13·p + 7) + 1933910820·p^14·z^24·(p － 1)^15·(8·p + 5) + 1170524970·p^15·z^22·(p － 1)^16·(11·p + 8) + 429874830·p^16·z^20·(p － 1)^17·(20·p + 17) + 4537567650·p^17·z^18·(p + 1)·(p － 1)^18 + 115997970·p^18·z^16·(p － 1)^19·(16·p + 19) + 81880920·p^19·z^14·(p － 1)^20·(7·p + 10) + 32256120·p^20·z^12·(p － 1)^21·(4·p + 7) + 4032015·p^21·z^10·(p － 1)^22·(5·p + 11) + 254475·p^22·z^8·(p － 1)^23·(8·p + 23) + 118755·p^23·z^6·(p + 4)·(p － 1)^24 + 819·p^24·z^4·(p － 1)^25·(4·p + 25) + 27·p^25·z^2·(p + 13)·(p － 1)^26 + p^26·(p － 1)^27)、

　わずか、0.062秒で求めることができたぞ。
　なお、上記は、zの54次方程式であるが、z^2＝x、と置くことにより、xの27次方程式に変換できる。
　当然ながら、一般のp に対して、解を求めることは、できないので、特定のpを固定して、解を求めることになるじゃろう」　
　目次へ戻る

（3）c＝54の固有方程式の解（根）

「前節の最後に掲げた54次方程式の解を求めてみたよ。
　おじぃさんが言ってくれたように、54次方程式は、z^2＝x、（x>＝0） とおくことにより、xの27次方程式に変換できる。
　でも、当然だけど、一般のpについて、解を求めることは、できない。
　そこで、今回は、テストを兼ねて、p＝1/2 と置いてみた。
　グラフは、こんな感じ。
　
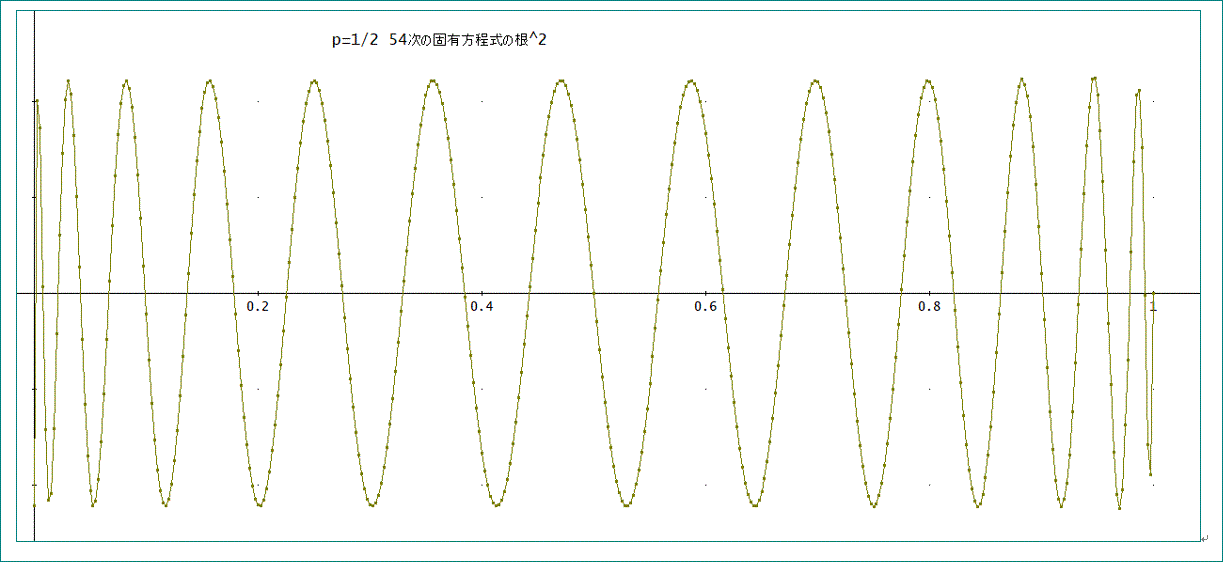
　なんか、音の波形みたいでしょ。
　横軸は、x 、縦軸は、Φの値、
　ゼロ付近の拡大図は、下の通り。
　
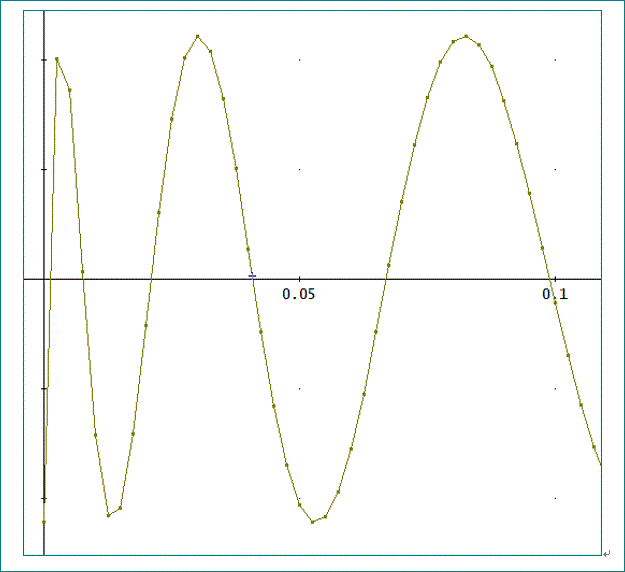
　グラフでは、xのゼロ及び1付近が分かりにくけど、後で挙げる数値を見ていただくと、解が27個あることが分かるわ。
　なお、元の固有方程式の解は、更に、z＝±√x 、となるため、正負併せて、54個となるので、注意してね。

　計算精度を20桁とする。
x ＝ 0.00084592086436589597608、1番目
x ＝ 0.0075961234938959703166
x ＝ 0.99915407913563410402
x ＝ 0.61530793537122008922
x ＝ 0.38469206462877991077、　　5番目
x ＝ 0.97899475615774443721
x ＝ 0.021005243842255562781
x ＝ 0.93301270189221932338
x ＝ 0.066987298107780676618
x ＝ 0.040891946559862992620、　　10番目
x ＝ 0.55804645706261511483
x ＝ 0.44195354293738488516
x ＝ 0.90106159637752189254
x ＝ 0.098938403622478107458
x ＝ 0.99240387650610402968、　　15番目
x ＝ 0.95910805344013700737
x ＝ 0.77475448903540301763
x ＝ 0.22524551096459698236
x ＝ 0.82139380484326966316
x ＝ 0.17860619515673033683、　　20番目
x ＝ 0.86368682078652434799
x ＝ 0.13631317921347565200
x ＝ 0.72439959010023108639
x ＝ 0.27560040989976891360
x ＝ 0.67101007166283436652、　　25番目
x ＝ 0.32898992833716563347
x ＝ 0.5、
と27個の解がある。
　ただし、大小まちまちとなっているので、番号に特に意味はないの。
　見にくくってごめんなさい。
　ちなみに、ゼロに最も近いのは、1番目の0.0008・・、1に最も近いのは、15番目の0.9924・・、でした。
　計算時間は、約0.73秒だったわ」

「なるほど。
　27個の根が単根であり、元の方程式の根は、正負のそれぞれ27個の単根であることとがよく分かった。
　いや、それにしても、DERIVEの計算は、速かったのう。
　ちなみに、誤差の大きさは、どの程度かを調べるために、5番目毎に方程式の残差を計算してみた。
1番目：　約9×10^(－37)
5番目：　約8×10^(－26)
10番目：約7×10^(－36)
15番目：約1×10^(－34)
20番目：約7×10^(－35)
25番目：約1×10^(－35)
27番目：0
　このように、誤差は、ずいぶんと小さいことが分かった。
　ちなみに、グラフの波の山の高さは、1×10^(－12)程度なのだ」
　目次へ戻る

（4）固有方程式の一般形

「（2）節の結果をもう一度、示すとこんな感じね。
　2以上の整数 c に対して、
　Φ(c)＝［－λ，－(1－p)］’・A^(c－1) ［1，0］‘、
　ここで、Aは、2次の行列で、
　
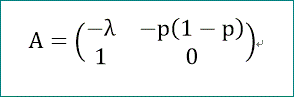
　により、固有方程式が求められるのね。

　ここで、第88回の『マルコフ過程（1）（非対称道中双六：宿場数＝3～9）』の『宿場数＝1（c＝2）の平均日数』を参考にする。
　行列 A を対角化して、Φをc、λ、p の陽なる式として、表すことを狙う。
　そのためには、2次正方行列 R を使って、
　R^(－1) A R＝B、の関係にある2次の対角行列 B と変換行列R を求める。
　
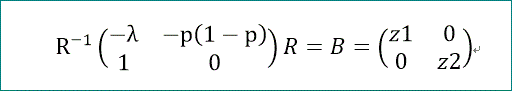
　ここで、z1、z2、は、Aの固有値である。
　
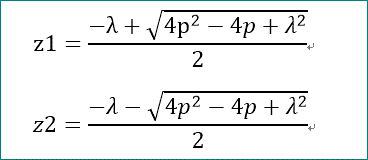
　このようなBとRがあれば、A^n は、R B^n R^－1 で計算できる。
　B^nは、対角要素のn乗の対角行列となるので、R B^n R^－1 を具体的に計算でき、Φ(c) を求めることができるという訳ね」

「なるほど。
　固有方程式を求める過程も、（小さな）マルコフ過程となっているのじゃな。
　うまくできているのう」

「固有値が求められたので、固有ベクトルを求めて、変換行列 R を求めるんだけど、
　やり方は、第88回と同じなので、ここでは、Rだけを示すわ。
　R＝([2·p·(1 － p)/(√(4·p^2 － 4·p + λ^2) + λ), 2·p·(p － 1)/(√(4·p^2 － 4·p + λ^2) － λ); －1, －1])
　
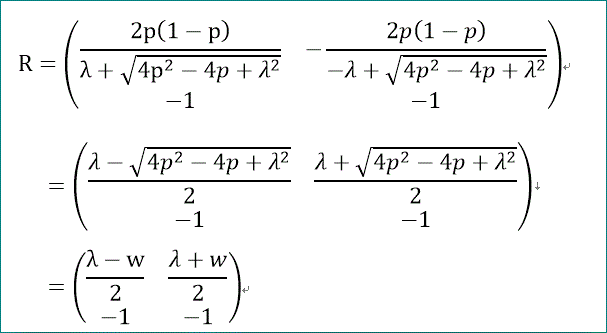
　ここで、1つ目から2つ目の式の変形で分母を有理化した。
　最後の式の中のwは、w＝√(4p^2－4p+λ^2)、ね、

　また、これから、
　R^－1＝([－ 1/√(4·p^2 － 4·p + λ^2), － (√(4·p^2 － 4·p + λ^2) + λ)/(2·√(4·p^2 － 4·p + λ^2)); 1/√(4·p^2 － 4·p + λ^2), (λ － √(4·p^2 － 4·p + λ^2))/(2·√(4·p^2 － 4·p + λ^2))])
　
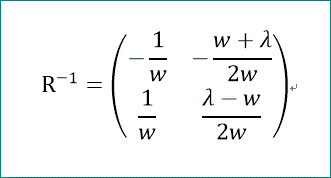
　試しに、R*R^－1を作って確認すると、
　
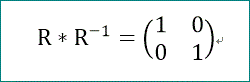
　が確認できた」

「じゃ、わしが、R^－1 A R を計算してみようかの。
　これは、([(√(4·p^2 － 4·p + λ^2) － λ)/2, 0; 0, － (√(4·p^2 － 4·p + λ^2) + λ)/2])
　となり、。
　
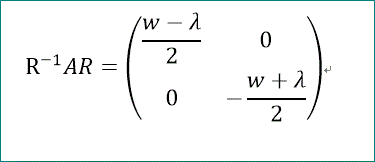
　これは、Bに等しいことが分かった」

「よって、A^n＝R B^n R^－1 を計算すると、
　
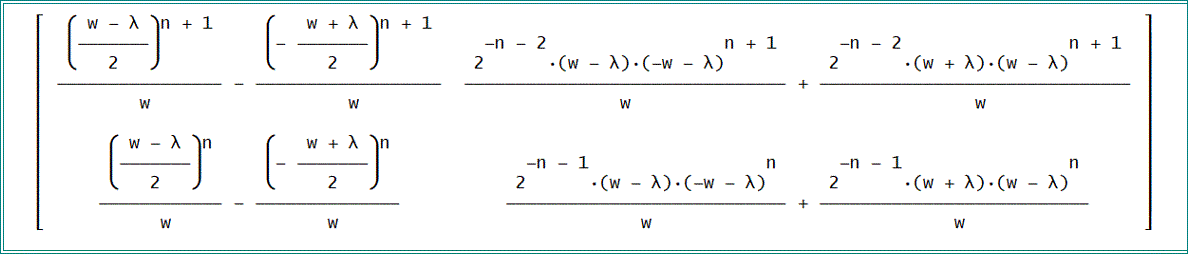
　ここで、nをc－1に変えて、
　A^(c－1)*［1，0］’ を計算すると、
　[((w － λ)/2)^c/w － (－ (w + λ)/2)^c/w, ((w － λ)/2)^(c － 1)/w － (－ (w + λ)/2)^(c － 1)/w]
　が得られる。
　最後に、［－λ，－(1－p)］’ との内積を計算すると、
　Φ(c)＝(2^(－c)·((w － λ)·(2·p + w·λ + λ^2 － 2)·(－w － λ)^c + (w + λ)·(w － λ)^c·(2·p － w·λ + λ^2 － 2))/(w·(w + λ)·(w － λ)))
　ただし、w＝√(4·p^2 － 4·p + λ^2)、である。
　
　DERIVE では、まとめてしまうので、分離しにくいんだけど、少し手伝うと、次の形に変形できる。
　Φ(c)＝(－ 2^(－c))·(λ^2 － 2· +2p))·((－1)^(c － 1)·(w + λ)^(c － 1) － (w － λ)^(c － 1))/w
　　　+ (－ 2^(－c))·(λ·((－1)^(c － 1)·(w + λ)^(c － 1) + (w － λ)^(c － 1)))、
　
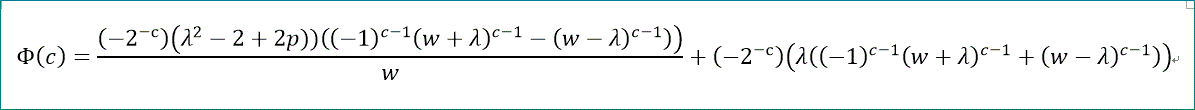
　と一般形が求められた」

「これは、素晴らしい。
　ともちゃん、お手柄じゃな」

「ありがとね。
　さて、Φの右辺の第1項の分子の左から3つ目のかっこ内の(w+λ)^(c－1)－(w－λ)^(c－1)を2項定理で展開すると、
　w^奇数×λ^(c－1－奇数)の多項式となるでしょ。
　このwをかっこの外にくくり出せば、分母のwと消しあって、第1項は、w^(偶数)×λ^(c－1－奇数)の多項式となる。
　w＝√(4·p^2 － 4·p + λ^2)、なので、wの偶数べきは、λ^2の多項式となる。（赤いべき記号が抜けていたので修正:2018/7/24）

　今、cが偶数であれば、c－1－奇数は、偶数となるため、第1項全体は、λ^2の多項式でしょ。
　また、cが奇数であれば、c－1－奇数は、奇数となるため、第1項全体は、λ×（λ^2の多項式）となる。

　次に、第2項のかっこの(w+λ)^(c－1)+(w－λ)^(c－1)は、2項定理で展開すると、
　w^偶数×λ^(c－1－偶数)の多項式となるので、wについては、偶数べきのみが現れる。
　今、cが偶数であれば、c－1－偶数は、奇数となるため、かっこの外にあるλを勘案すれば、第1項全体は、λ^2の多項式なのね。
　また、cが奇数であれば、c－1－偶数は、偶数となるため、かっこの外にあるλを勘案すれば、第2項全体は、λ×（λ^2の多項式）となる。
　
　よって、cの偶・奇によるΦの形の違いは、第91回で扱ったけど、Φの一般式から、同様のことが証明されたと言えると思うわ」

「なるほどのう。
　Φの一般形から言われると納得じゃな。
　DERIVEの関数は、作ってみたかいな」

「実は、少し手間取ったの。
　DERIVEさんは、式をまとめたがるのよ。
　かえって、計算に時間がかかってしまったの。
　最初は、次のように、Φnew2 を定義してみた。
　Φnew2(x_，n_)：＝
　　　PROG(
　　　　　IF(INTEGER?(n_) ＝ false, RETURN "Not Integer"),
　　　　　IF(n_ < 2, RETURN "Number < 2"),
　　　　　w_ ≔ √(4·p^2 － 4·p + x_^2),
　　　　　2^(－n_)·(w_ － x_)^(n_ － 1)·(2·p^2 － w_·x_ + x_^2 － 2)/w_ + 2^(－n_)·(w_ + x_)^(n_ － 1)·(2·p^2 + w_·x_ + x_^2 － 2)·(－1)^n_/w_
　　　　)
　c＝54では、Φnew2では、約42秒を要した。
　そこで、計算を2段階に分けて、次のように行うことにした。
　Φnew2(x_, n_):＝
　　PROG(
　　　　IF(INTEGER?(n_) ＝ false, RETURN "Not Integer"),
　　　　IF(n_ < 2, RETURN "Number < 2"),
　　　　f_ ≔ (－ 2^(－n_))·(x_^2 － 2 + 2·p)·((－1)^(n_ － 1)·(w_ + x_)^(n_ － 1) － (w_ － x_)^(n_ － 1))/w_,
　　　　LIM(f_ + (－ 2^(－n_))·(x_·((－1)^(n_ － 1)·(w_ + x_)^(n_ － 1) + (w_ － x_)^(n_ － 1))), w_, √(x_^2 + 4·p^2 － 4·p))
　　)
　これで、Φnew2 のc＝54の場合の計算時間が 0.06秒程度と（2）節のΦnew と同一レベルに高速化できたわ」
　目次へ戻る

最終更新日　2018/7/9　一部修正 2018/7/10・11、2018/7/24