(1) 概要
(2) 対称式
① 対称式とは
② 基本対称式とは
③ 同次対称式を基本対称式で表す
④ 基本対称式を同次対称式で表す
(3) 対称式を基本対称式に分解
① 代数方程式 小史
② ウェアリングの方法
(4) 平均日数計算へのウェアリングの方法の適用
① c=4(宿場数=3)
② c=6(宿場数=5)
③ c=8(宿場数=7)
④ c=10(宿場数=9)
(5) 平均日数公式と対称式、ユーザー定義関数
① 平均日数公式は対称式である
② 平均日数公式の分母
③ Ψが多項式となる理由
④対称式を基本対称式に分解するユーザー定義関数
※ c=宿場数+1
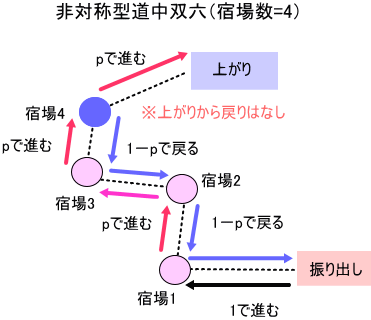
第90回『マルコフ過程(3)(非対称型道中双六:平均日数計算公式)』で導いた平均日数公式には、固有方程式の根が含まれています。しかし、c(=宿場数+1)が10以上の推移確率行列の固有値方程式は、固有値の2乗を新変数としても、5次以上となり、変数係数のままでは、一般には、その根を求めることは、できません。従いまして、これまで、cが10以上では、平均日数を根の数値計算に頼らずに方程式の係数や最後の宿場の初期の状態ベクトルの複数の値のみで表すことは、できないと考えてきました。

そんな中、第91回『マルコフ過程(4)(非対称型道中双六:固有方程式の漸化式)』において、たまたま触れた『判別式』は、定義に方程式の根を使っていますが、その値は、根の計算をせずとも、方程式の係数のみで表すことができます。また、第88回『マルコフ過程(1)(非対称型道中双六:宿場数=3~9)』では、平均日数の厳密解(c=2~4)及び数値計算(c=5~10)から予想式を求め、係数を観察したところ、様々な特徴があることが分かりました。(注)厳密解は、その後、c=5~6を求めて、予想式と一致することを確認しました。
ちなみに、c(=宿場数+1)=2s、s=1,2,・・となる偶数の場合、平均日数は、次式で表されます。
xiは、推移確率行列Aの2s次の固有方程式で、固有値λの2乗をxに置き換えたs次の方程式の根を表す。
※ 今回は、偶数の場合を中心に考えますので、cが奇数の式は、第90回をご参照ください。
係数diは、次の2つの関係式から求めることができます。
ここで、m=0、1、・・s-1、の整数。
Uは、[U1(t),U2(t),・・,U2s(t)]と書ける状態ベクトル。1が振り出しを、c=2sが上がり前にある最後の宿場を表します。
なお、Uの初期値は、[1,0,0,・・・0]とします。
さて、平均日数をpの関数としてみたとき、その特徴をいくつか挙げますと、
(1) c=宿場数+1としたとき、平均日数の式は、『有理関数』であり、その分母は、p^(c-1)、である。
(2) 平均日数の式の分子は、pの整数係数の多項式であり、
cが偶数の場合は、pの(c-2)次の多項式、
cが奇数の場合は、(c-1)次の多項式で、(c-1)次の係数は、1である。
(3) 分子の定数項は、2であるなどです。
これらのことから、第91回の最後に『平均日数の計算式も、方程式の根が含まれているが、ひょっとすると、係数のみで書くことができるかもしれん』と書いた訳です。ところが、第92回『マルコフ過程(5)(非対称型道中双六:固有方程式の一般形)』において、目標である『東海道五十三次』の非対称型道中双六の平均日数を求める際に必要となると思われる変数係数の54次の固有方程式も1秒未満で書き出すことができ、その54次方程式の根の2乗を新変数とする27次方程式の根も、推移確率pを数値で指定すれば、同程度の時間で求められことが分かりました。これにより、任意のpに対する平均日数を精密に数値計算したいという欲求は、原理的には、満たされたことになり、前掲の『平均日数を・・かもしれん』という点の追求を怠ってまいりました。
しかし、2018年8月の第92回以降『ボーッと生きてきた』1年を反省し、当時、感じていたモヤモヤ感を払拭すべく、本稿を書くにあたり、再考したところ、遅まきながら、(固有方程式の根の2乗を新変数とした)方程式の係数と最後の宿場の状態ベクトルのいくつかの値のみで、平均日数を構成できること、すなわち、平均日数をpの関数として表せることが分かりました。今回は、そのことを中心に書きたいと思います。
さて、そんな、都合の良いことが起きるのは、平均日数公式が方程式の根に関して『対称式』であることによります。『対称式』が『基本対称式』の多項式で表されることは、(対称式に関する)代数学の基本定理で保証されています。その結果、平均日数の計算は、数学的には、対称式を基本対称式に分解する問題に帰着されました。すなわち、基本対称式で表せれば、方程式の根と係数の関係から、基本対称式が方程式の係数で表されるため、平均日数の計算式の厳密解を求めることができるという訳です。
今回、c=8(宿場数=7)の場合(※)を、対称式を基本対称式の多項式に分解する『Waring(ウェアリング)』の方法を使って、平均日数の厳密解を求めることができ、有効性が分かりました。なお、c=8の場合については、これまで、DERIVEにより、平均日数公式に(固有方程式の根の2乗を新変数とする)4次方程式の根を使って、計算させていましたが、変形が思うように行かず、やむなく、pを1/3などと有理数で与え、その後、厳密に計算していた経緯があります。もっとも、DERIVEの式変形を人が手伝ってあげれば、変形できた可能性は、ありますが、その部分は、今回取り上げた基本対称式に分解することに通じると思われます。
ということで、ようやく、問題解決の玄関に入ったとは、いえるでしょうが、目標の五十三次では、27変数、27次の対称式を基本対称式に分解する話となります。変数係数の対称式となりますと、途中の計算で発生する項の総数が途方もない大きさになる可能性もあり、難しいかもしれません。やはり、今回や前回までの結果等を踏まえて、何らかの漸化式を導くことが近道でしょう。仮に数値計算で良ければ、27次方程式の根を使った計算の方が現実的かも知れません。
※c=10(宿場数=9)の場合もウェアリングの方法にて平均日数の計算を行い、推定式と一致することを確認しました。(2019/8/18追記)
「対称式とは、式の中で使われている変数を互いにどのように交換しても値が変わらない式のことを言うのじゃな。たとえば、x、yの2変数であれば、x+y、(x^2+y^2)、や、(x-y)^2+3xy、などは、対称式じゃな。なお、変数を交換したときに符号のみが変わる式は、『交代式』と呼ぶそうじゃ」
 「1年間も、ずいぶん、ボーッとしてたじゃない!」
「1年間も、ずいぶん、ボーッとしてたじゃない!」
「おう、ともちゃんかい。今年の8月の暑さは、格別じゃな。また、間が空いてしまった。とは言え、ともちゃんに頼んでおる『行列式の巻』も、なかなか、進まないようではないかのう?」
「まぁ、たしかに。それを言われると、わたしも、つらいわ、苦しいの。えーと、問題をそらす、じゃない、問題解決の決め手が対称式ということに、驚いたわ」
「そうじゃろう。ナントの勅令なみに、わし自身が驚いた。高校の頃は、式の展開や因数分解は、習ったものの、取り立てて、対称式、基本対称式などの概念は、習わなかったと思うがのう。今は、高校で、ある程度、基礎的なことを習っているようだ。
わしが気がついたきっかけは、2019年の5月以降、この問題を再考しているとき、判別式と平均日数公式とのある種の類似性について、何かヒントを探すために、インターネットで方程式、根などと入力して、検索していたところ、運良く下記のページに行き当たったことだ。
『対称式の真実』
http://shochandas.xsrv.jp/polynomial/symmetric-p.htm
後で分かったが、このページは、『私的数学塾』というサイトのページで、すでに当方の『私撰ページ』にリンクを貼っていた。いや、灯台もと暗し、とはこのことだな。このページを一読させてもらうと、まさに今回のために、書かれているのではないかと思うほど、ぴったりな内容で、感激したのじゃよ」
「基本対称式は、2変数であれば、x+y、xy、のペアのことよね?」
「そのとおり。以下では、変数名として、これまで使ってきた、x1、x2などを使うことにする。本来は、x1、x2などと下添え字を使うべきじゃが、なかなか面倒なので、勘弁していただきたい」
「判別式を取り上げたときに、代数方程式の根と係数の関係も取り上げたじゃろう。前掲のページでも解説されているように、基本対称式とは、符号を除いて、根と係数の関係に表れる式に等しいのだな。
実は、『対称式の真実』を読むまで、わしは、こう思ってきたのじゃ。『x1+x2=-a1、x1x2=a0、などの基本対称式(この用語は知らなかったが)から作られる任意の多項式や関数をa0、a1などで表せるのは、自明だ。だが、任意の式、たとえば、平均日数公式を基本対称式で表せるかどうかは、不明だな』と。
しかし、このページでは、『対称式は、基本対称式の多項式として表せ、その表し方は、一意である』ことが代数学の定理であるとはっきりと書かれていることに気がついたのじゃ。その後、手元の本で調べたところ、対称式が基本対称式の多項式で表されることは、『対称式に関する基本定理(fundamentaltheoremonsymmetricpolynomials)』により保証されている。』(岩波数学辞典第4版『多項式』P802~804)と記載されていたのだな」
 「おじぃさんの感動が大きすぎて、話が進まないので、あたしが簡単にまとめるわよ。
「おじぃさんの感動が大きすぎて、話が進まないので、あたしが簡単にまとめるわよ。
『対称式』とは、x1等の変数の番号の任意の入れ替えで不変な値を持つ式のことね。例えば、x1+x2は、x1とx2を交換しても、その式の値は、変わらない。また、x1*x2も同様である。(煩雑なので、積の記号*は、省略して、半角のスペースで表すわ)
あ、一つ注意ね。n個の変数の入れ替えは、n!/2通りもあるの。だけど、そんなにたくさんの場合を調べる必要は、ないのね。任意の変数の入れ替え、すなわち、『置換』は、複数の『互換』を続けて適用すれば、実現できるので、互換の総数、n(n-1)/2通りについて、調べれば、いいのよ。互換を偶数個続けて実現できる置換を『偶置換』、奇数個続けてできる置換を『奇置換』と呼ぶことも、よく知られているわ。
さて、一般に、n個の変数、x1~xnを考えて、その基本対称式、s1、s2等を次で定義します。
s1=x1+x2+・・xn、n個の変数の和、
s2=x1x2+x2x3+・・xn-1xn、相異なる2個の積の和、
s3=x1x2x3+・・、相異なる3個の積の和、
以下同様、
sn=x1x2・・xn、すべての変数の積、
例えば、n=2の場合は、s1=x1+x2、s2=x1x2、とするということよ。
このとき、x1^2+x2^2を基本対称式で表すと、x1^2+x2^2=(x1+x2)^2-2x1x2=s1^2-2s2、であることが分かる。
でも、知りたいのは、なぜ、基本対称式をこの形に選んだの?、ってこと。それは、皆さまもお気がつかれることでしょうが、x1等をn次の代数方程式の根と考えたとき、基本対称式をこの形に選べば、根と係数の関係と直接結びつくからよね。
実際、(最高次の係数が1の方程式をモニックという)2次方程式は、その根x1、x2により、(x-x1)(x-x2)=x^2-(x1+x2)x+x1x2、と表すことができる。この2次方程式の2つの係数と基本対称式(赤色のx1+x2、青色のx1x2)とは、符号を除いて等しいでしょ。3次以上でも事情は、同じ。それがどうしたって?、こうすると、いろいろと都合が良いことが起こりそうじゃない!。
でも、ニュートンの名前が付いた『同次対称式』というのもあるのよ。n変数として、それをTn等で表すと、
T1=x1+x2・・+xn、これは、n変数のときのs1と同じ。
T2=x1^2+x2^2+・・+xn^2、各変数の2乗の和
以下同様、
Tn=x1^n+x2^n+・・+xn^n、各変数のn乗の和よ。
この同次対称式とさっきの基本対称式との関係を示したのが、次の『ニュートンの多項式』ね。
n変数の場合、s1~snを基本対称式、T1~Tnを同次対称式とすれば、
Tn-s1Tn-1+s2Tn-2-+・・・+(-1)^(n-1)sn-1T1+(-1)^(n)sn×n=0、の関係が成り立つ。
なお、下添え字がゼロまたは負となる項は、存在しないものと見なします」
「ともちゃん、ありがとさん。これまで、ほぼ、話だけだったので、具体的な例を挙げることにしよう。
まずは、3変数の場合、同次対称式と基本対称式の関係だ。
その前に注意がある。以前にも書いたが、半角のハイフンマイナス符号は、見づらいので、全角の-に置き換えてあります。
ページ内の式をコピーして、DERIVEなどで再計算に利用する場合は、あらかじめ、全角の-を半角の-に全置換してください。また、乗算記号(ドット)も半角のスペースに置き換えている場合もありますので、注意してください。なお、+は、半角のままです。
3変数の場合の基本対称式は、次の3つである。
s1=x1+x2+x3
s2=x1x2+x2x3+x3x1
s3=x1x2x3
すると、同次対称式は、
T1=x1+x2+x3=s1
T2=x1^2+x2^2+x3^2=(x1+x2+x3)^2-2x1x2-2x2x3-2x3x1=s1^2-2s2
T3=x1^3+x2^3+x3^3
=(x1+x2+x3)(x1^2+x2^2+x3^2)-x1x2^2-x2x3^2-x3x1^2-x1x3^2-x2x1^2-x3x1^2
=s1(s1^2-2s2)-x1x2(x1+x2+x3)-x2x3(x1+x2+x3)-x3x1(x1+x2+x3)+3x1x2x3
=s1(s1^2-2s2)-s1(x1x2+x2x3+x3x1)+3s3
=s1(s1^2-2s2)-s1s2+3s3
=s1^3-3s1s2+3s3、となる」
 「3変数でも、ごちゃごちゃした式になってしまうのね。こりゃ、とうてい、27変数は、無理でしょう」
「3変数でも、ごちゃごちゃした式になってしまうのね。こりゃ、とうてい、27変数は、無理でしょう」
「ともちゃんや、もう、27変数のときの心配かいな。まずは、4変数の場合じゃ。
4変数の場合、基本対称式は、次の通り。
s1=x1+x2+x3+x4
s2=x1x2+x2x3+x3x4+x4x1+x2x4+x1x3
s3=x1x2x3+x2x3x4+x3x4x1+x1x2x4
s4=x1x2x3x4
同次対称式は、次の通りじゃ。
T1=x1+x2+x3+x4=s1
T2=x1^2+x2^2+x3^2+x4^2=(x1+x2+x3+x4)^2-2s2=s1^2-2s2
※ T2は、3変数でも、4変数でも、s1^2-2s2、と同じになるのは、不思議ポイント。不変式というそうな。
T3=x1^3+x2^3+x3^3+x4^3=s1T2-s2T1+s3T0=s1^3-3·s1·s2+3·s3
T4=x1^4+x2^4+x3^4+x4^4=s1T3-s2T2+s3T1-s4T0=s1^4-4·s1^2·s2+4·s1·s3+2·s2^2-4·s4」
「前に触れたニュートンの多項式の関係を使うと逆に、基本対称式を同次対称式で表すこともできる。
たとえば、n=2では、
T1=x1+x2=s1
T2=x1^2+x2^2=s1^2-2s2
から、
s1=T1、
s2=(-T2+T1^2)/2、と求められる。
nが3変数の場合は、
T1=x1+x2+x3=s1
T2=x1^2+x2^2+x3^2=s1^2-2s2
T3=x1^3+x2^3+x3^3=s1^3-3s1s2+3s3
よって、
s1=T1
s2=(-T2+T1^2)/2
s3=(-T3+T1^3-3s1s2)/3=(-T1^3+3T1T2-2T3)/2
と書き表せる」
 「この逆のケースは、どんなときに役立つのかしら?」
「この逆のケースは、どんなときに役立つのかしら?」
「そのご利益は、如何にじゃな。これは、大いにある。後で出てくるが、ウエアリングの方法で(あってもなくても)多数の項を持つ多変数多項式を変形していくのは、手計算では、大変じゃ。(昔の方は、偉かったな。)そこで、PCで機械的に計算したいのだが、DERIVEでは、基本対称式を自動的に生成するのが難しかった。もちろん、変数の個数nが小さい場合、手作業で配列に入力してしまった方が手っ取り早い。しかし、一般のnについて、その自動生成が面倒なのじゃ。そんな折り、同次対称式から計算させることができて助かった。同次対称式は、Tj=Σ(k=1~n)(xk)^j、ただし、j=1~n、と容易に定義、計算させることができたからのう」
「へー、そんなことが。もう一つ、質問だけど、対称式を基本対称式に分解する方法は、そのウェアリングの方法だけしかないの?」
「よくぞ、聞いてくれましたな。先に調べた『対称式の真実』では、ウェアリングの方法が紹介されていたが、ウィキペディアの『対称式』を参照すると、『ウェアリングによる方法』の他に『コーシーによる方法』、『斉重対称式』の2つの方法が例とともに紹介されていた。最後の『斉重対称式』による方法は、その創案した方のお名前がないのは、なぜなのか?、とか気になる点もあるが、ウェアリングの方法以外は、後日、時間があれば、取り上げよう。でないと、今回の分量が多すぎてしまうからのう」
「1次方程式については、すでに紀元前1800年~2000年頃のエジプトの遺跡から、当時の人が(原理的には)その解法を知っていた記録が発見されているそうだ。以前に紹介したこともあるが、ax=b、は、分数を使えば、解くことができる。ピラミッドの高さなどを測量で測定するためには、必要なことだったろう。ただ、負の数は、使われていなかったようだ」
 「矢野先生の『数学史』(科学新興社:矢野健太郎著:1967年初版第1刷)では、リンド(=発見者名)パピルス、あるいは、作者の名前と思われるアーメスのパピルス(パピルスは、葦から作った紙ね)に書かれているのが、2/5=1/3+1/15、2/7=1/4+1/28、などの分子が1でない分数を分子が1の単位分数の和で表した表が載っている。
「矢野先生の『数学史』(科学新興社:矢野健太郎著:1967年初版第1刷)では、リンド(=発見者名)パピルス、あるいは、作者の名前と思われるアーメスのパピルス(パピルスは、葦から作った紙ね)に書かれているのが、2/5=1/3+1/15、2/7=1/4+1/28、などの分子が1でない分数を分子が1の単位分数の和で表した表が載っている。
また、『ある数とその1/3を加えたものが24である、ある数はいくつか?』という問題も書いてあるそうよ。今の記法ならば、x+x/3=24、ということよ。当時は、xを3と仮定せよ。しからば、左辺は、4となる。しかし、これが24となる必要があるので、すなわち、24/4=6倍とすると、xは、3の6倍の18である。こう解いていたらしい。仮定法と呼ぶとのこと」

「なるほど。ともちゃん、よく、矢野先生の『数学史』に気がついてくれましたな。装丁に傷みが出てきたし、字が小さいので、以前、スキャンしてハードディスクに格納しておったのじゃ。詳しく書かれておるのう。平面図形の面積や立体の体積についても、リンド・パピルスに載っているそうだ。特に円の面積の例では、円の面積=(直径-直径/9)^2、という式が載っている。これは、当時、円周率を(16/9)^2≒3.16、とエジプトの人達がとらえていたことを示している。2桁合っていることは、すごいのう。
その後、ともちゃんも知っているように、エジプトで作られた数学や技術知識が古代ギリシャに受け継がれた。ギリシャ七賢人の一人と言われる『ターレス』(紀元前624年頃~紀元前546年頃)は、エジプトの実用的な数学を受け継ぎつつ、理論的な再構築を行った。それを継いだ『ピタゴラス』(紀元前582年頃~紀元前493年頃)などが、ピタゴラス学派と称される組織を作って研究にいそしんだ。例えば、音楽の弦楽器の弦の長さを1/2と短くすると、音の高さ(今日の振動数)が2倍となることを発見している。これが1オクターブの由来となった。ピタゴラス音階という言葉も後世生まれている。
ピタゴラスは、有名なピタゴラス数(3^2+4^2=5^2などの3つの数の組)のように数の2乗や3乗も考えた。また、当時の人々は、エジプトから引き継いだ図形の面積や体積の問題も扱った。今で言う、無限和の考え方も生まれた。その結果、例えば、辺の長さが1の正方形の対角線の長さ(√2≒1.41421356・・)が有限の分数では、表せないことを証明する者も現れた。ギリシャ以前であれば、それは、大した問題ではなかったろう。概略、√2≒1.41程度で実用上は、十分だったろうからな」
「√2が分数で表せないからと言って悩む必要はなかったのにね。しかし、ピタゴラス学派にとっては、こいつは、都合が悪い事実だったので、この証明者は、追放されたとも、殺されたとも言われているほど。とは言え、2次方程式を解くために、今で言うところの平方完成が使われていた。だけど、その解を表すには、整数や分数だけでは、足りずに、少なくとも、√2のような無理数が必要となったのは、重要ね」
「1次方程式について、体系的に論じたのは、西暦825年前後(こりゃ、だいぶ、経ってからのことだ)のインドの数学者『アルクワリズム』(現代の『アルゴリズム』の語源となった人)が著した『アルジャブルワルムカーバラ』だそうじゃ。英語で代数学を意味する『Algebra』は、この本のアルジャブルという名前に由来すると言われている。同書は、後にラテン語に翻訳されて、ヨーロッパに伝わった。(『数学・物理100の方程式』日本評論社1989年の『代数方程式』の項による)
と、まあ、この調子で書いていくと、とても大変なので、端折ろう。3次方程式については、第12回3次方程式、で触れている。これは、『タルタリアの解法』として知られている。イタリアの(通称)タルタリアからその解法を聞き出したカルダノが自分の著書で1545年に公開してしまったと言われている。ここまで、2次方程式から相当年数が経過している。もちろん、その間、3次や4次方程式を解く必要が無かった訳もなく、因数分解可能な方程式は、解かれていたろうし、それ以外は、数表を使って計算していたと思われるので、実用的には、特に困らなかっただろう。ルネサンス以降、キリスト教の呪縛を離れて、様々な学問が発展する中で、方程式の理論的な解法が進展した背景には、当時、数学の問題を出し合って、勝負することが流行していたことがあったようだ」
「数学の勝負って、日本でも、たしか、『算額』というのがあったような?」
「算額というのは、明治以前の日本の和算における風習のことじゃな。『だから楽しい江戸の算額』(小寺裕著:研成社:2007年9月第1刷)に詳しい。同書によれば、『算額』という絵馬の一種を神社仏閣に奉納する習慣は、17世紀頃から起こったらしいと書かれている。目的は、数学の勝負というより、和算家としての自らの業績等を発表するメディア(今であれば、Webページ)として利用されていたらしいことが分かる。現存する最古の算額は、栃木県佐野市の星宮神社にあるもので、村山庄兵衛吉重 奉納、1683年のものだそうじゃ。1975年に火災で焼失したが、その後、復元された。なお、数学の勝負と言えば、同書には、『遺題継承』という慣習についても記載されている。先人の著した書籍の解答のない問題(=遺題)の解答を自分の書籍に載せるという習慣だ。これは、先人の挑戦に対する勝負とも考えられる。有名な和算書である『塵劫記』(吉田光由著:初版1627年)の改訂版(1641年)で巻末に解答のない12問の問題を付けたことに始まるそうだ」
「へー。そういえば、映画の『天地明察』(2012/9の角川/松竹映画(監督=滝田洋二郎:出演=岡田准一、宮崎あおい他)にも、算額や和算家が出てきてた。和算や算額にスポットライトが当たったと思うわ。
ところで、4次方程式は、第13回4次方程式で扱ったけど、細かなことで疑問があるわ。それは、『数学・物理100の方程式』では、カルダノの著書は、1575年となっているけど、矢野先生の数学史では、1545年となっていることね」
「ほんとうじゃな。『数学史』では、『タルタリアは彼の発見したこの3次方程式の解法を公表はしなかったが,ミラノのカルダノ(HieronimoCardano,1501-1576)の非滞に熱心な頼みにまけて,絶対他へは公表しないという約束で,これをカルダノヘ教えた.ところがカルダノは,この約束を破って,彼が1545年に発表した彼の書物ArsMagnaのなかへ,この解法をのせてしまった』と書かれている。
一方、『数学・物理100の方程式』の代数方程式の項では、アルスマグナ(1557)と記載されている。ではと、『数学辞典』(岩波書店:第4版)の『ルネッサンスの数学』の項を参照すると、アルスマグナは、1545年となっていた。
ウィキペディアの『ジェロラモカルダーノ』の項も参照したが、アルスマグナ(『偉大な術』という意味)は、1545年と書かれている。ということで、一応、上では、1545年としておいた。もしかすると、1545年の原版と異なる言語で、1575年に再出版されたのかも知れない。(重版出来か!)
しかし、このウィキのカルダノに関する記事は、面白い。矢野先生の本だけ読むと、カルダノは、他人から教えてもらったことを自分の著書に無断で載せてしまった(けしからん)賭博師としか思えんが、このウィキの記事を読むと、数学以外でも医学や機械技術の分野でも、当時、イタリアで認められていた人物で、医師で大学教授でもあったことが分かる。カルダノの父が『ダ・ヴィンチ』(1452年~1519年)の友人だったというあたりも、ルネサンスという時代が垣間見えて興味深い」
「トランプさんなら、『3次方程式の解き方を見つけたのは俺だ!』とすぐ、ツイッターに投稿しちゃいそうだものね」
「あはは、たしかにのう。同書には、カルダノの弟子のフェラリによるともいわれる4次方程式の解法も記載されているそうだ。アルスマグナ以前は、このような解法は、秘術とされて、師匠から弟子に秘密裏に伝わり、公開されなかった。この著書以降、だんだんに世間に公開されていくように変化していったということじゃ。と、ま、ここまでが前置きじゃ。すなわち、4次方程式の解法は、1545年以降に世間に知られるようになったのだ。
それ以降、多くの人が5次方程式の解法を求めたのは、当然じゃが、その解法を得ることはできなかった。そんな中、イギリスの数学者で、1760年からケンブリッジ大学のルーカス教授職(『ケンブリッジ大学の数学関連分野の教授職(ポスト)のひとつで、ヘンリー・ルーカスによる資金提供によって1663年に設けられたものである。ニュートン、バベッジ、ストークス、ディラック、ホーキングなどが務めたことで、きわめて名誉ある学術的地位とされている。』ウィキペディア)に就いていた、ウェアリング(EdwardWaring:1736~1798)が対称式が基本対称式の多項式に分解できることを発表した。1762年のことだそうだ。
アーベルによる『5次方程式には、代数的な解法が存在しない』という論文が出たのは、1826年のことだから、1760年頃から見れば、まだ、約60年も未来の話になるのだ。とは言っても、1760年頃は、4次方程式の解法が発見された1545年から約115年を経過し、そろそろ、5次方程式の根の公式は、見つからないのではないか、という気分も漂っていたと想像できる。そういう空気の中で、ウェアリングが生きていたんだな」
「つまり、ウェアリングが対称式や基本対称式など代数を研究していたのは、5次方程式の解法を得られるかも知れない、あるいは、その公式が存在しないことを証明できるかも知れないとも思っていたということかしら」
「そのあたりは、もちろん、分からないが、4次方程式までの宝探し的な解法術に磨きをかけるだけでは、5次方程式は、解けないと悟っていたのかも知れない。そのため、そもそも、代数方程式とはなんぞや、その根の性質は、どうなっているのか、などに関心が移っていったということじゃろう。実際、フランスのラグランジュは、2次~4次方程式の根の公式がなぜ、うまく導けたのかを研究して、『一般方程式』を考察し、根の置換と方程式の可解性について重要なヒントを得たというからのう。(青字の個所は、『数学・物理100の方程式』によります)」
※ウェアリングは、現代では、整数論の『ウェアリングの問題』で広く知られている。
『Waringの問題:自然数k,s,nに対して,n=m1^k+···+ms^kを満たす0以上の整数m1,···,msの組の個数をRk,s(n)とする。各kに対し,‘すべての自然数nに対してRk,s(n)>0’となるsの最小値をg(k),‘十分大きいすべてのnに対してRk,s(n)>0’となるsの最小値をG(k)でそれぞれ表す.J.L.Lagrangeの4平方数定理(1770)によりg(2)=G(2)=4である.E.Waringが著書(1770)にg(3)=9,g(4)=19を意味することを記してから,自然数をベキ乗数の和で表すことが研究されるようになり,それに関連する様々な問題を総称して現在ではWaringの問題といっている』(岩波数学辞典第4版P181)
ウェアリングの問題については、『数学100の問題』(日本評論社:1984)の中でも解説されている。
※平方数とは、4(=2^2)、9(=3^2)のように非負の整数の2乗で表される数、立方数とは、8(=2^3)、27(=3^3)など整数の3乗で表される数を指す。
ともちゃんとの対話で話を進めてきましたが、このあと、分量が多くなるため、このあたりで、ともちゃんには、休んでもらいましょう。
さて、対称式を基本対称式で表すためのウェアリングの方法を説明します。
変数の個数は、n、基本対称式は、s1~sn、とする。
対称式をψ(x1,x2,・・,xn)=単項式1+単項式2+・・・、と書く。単項式とは、係数×変数のべき乗の積のことです。
たとえば、2x1^2x2^3は、単項式。しかし、3x1^2+x2^2は、2つの単項式の和なので、これは、単項式ではない。
『単項式』というと難しく聞こえますが、次数が同じものの係数をかっこでまとめて一つの係数として変数のべき乗に掛けた項を指すものです。
多項式の初項を1として勘定して、j番目の単項式が、cjx1^a1(j)x2^a2(j)・・xn^an(j)、で表されるものとする。(cjは、係数。)
ここで、j番目の「次数」をdeg(単項式)=(a1(j),a2(j),・・an(j))で表す。
このdeg、かっこ内の左側の数字ほど高く、同じ位置であれば、数字が大きいほど、『次数』が高いと考える。
すなわち、(2,2,0)>(1,3,1)などと約束する。(辞書式順序と呼んでいる)
また、deg(ψ)は、多項式ψで、次数のもっとも大きい単項式の次数を表し、その項の順番をm、係数をcmとする。
ウェアリングの方法は、ψからdeg(ψ)に対応した基本対称式のべき乗の積を引き、その都度、deg(Ψ)が減少し、最後に定数が残ることを利用する。この結果、元のψは、残った定数+引き去った式の和というのがその仕組みである。
今、もっとも次数の高い単項式が、cx1^a1x2^a2・・xn^anとするとき、
差し引く式gとして、g=cs1^(a1-a2)s2^(a2-a3)・・sn^(an)、とおく。ここで、係数cやa1等の添え字jは、省略して書いています。
ちなみに、DERIVEで多項式を計算すると、いわゆる式の簡約化(因数分解等)が行われるため、単項式毎にバラけません。そこで、式を単項式に「展開」する必要がある。このとき、展開する変数(x1,x2,・・)は、その都度、指定する必要があるが、その並び順は、あらかじめ定められた変数名の優先度が高い順に並べられる。これは、(ウェアリングのいう)辞書式順序となるので、展開した式の第1項が式の最大次数(deg)の項となる。これは、ウェアリングの方法を適用するためには、好都合である。
しかし、今回のように変数名が、x,y,zでない場合、DERIVEのオプションのモード設定で変数の優先順序を『x1,x2,x3,・・』と変更しておかないといけない。
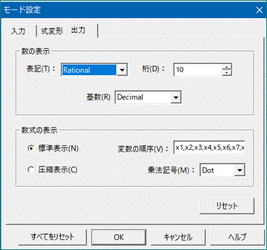
上の図の変数の順序の項目を変更(消去、追加する。変数名と変数名との間は、カンマで区切る)
これは、コマンド欄で、VariableOrder≔[x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,・・]と入力することと同等である。
例1 2変数の場合
ψ(0)=x1^3x2^2+x1^2x2^3-x1^2-x2^2、を基本対称式に分解する。
(この多項式は、ウェアリングの方法を説明するためのもので、特別な意味は、持ちません。)
各項の次数は、(3,2)(2,3)(2,0)(0,2)である。このとき、最も高い次数、deg(ψ(0))は、(3,2)であり、係数は、1、項の番号は、1である。
従って、差し引く式g(1)は、g(1)=1×s1^(3-2)×s2^2=x1^3·x2^2+x1^2·x2^3、
よって、新しいψ(1)は、
ψ(1)=ψ(0)-g(1)=x1^3x2^2+x1^2x2^3-x1^2-x2^2-g(1)=-x1^2-x2^2、
最も高い次数、deg(ψ(1))は、(2,0)であり、たしかに次数は低下している。係数は、-1、項の番号は、1である。
g(2)=-1×s1^(2-0)×s2^0=-(x1^2+2x1x2+x2^2)、よって、新しいψ(2)は、
ψ(2)=-x1^2-x2^2-g(2)=2x1x2
同様に、最も高い次数、deg(ψ(2))は、(1,1)であり、係数は、2、項の番号は、1である。
g(3)=2×s1^(1-1)×s2^1=2x1x2、よって、新しいψ(3)は、
ψ(3)=2x1x2-2s2=0、となり、定数となる。
従って、ψ(0)=残った定数(=0)+g(1)+g(2)+g(3)、となるので、
Ψ(0)=0+s1s2^2+(-s1^2)+2s2=s1s2^2-s1^2+2s2、となる。
右辺を展開して確認すると、(x1^3·x2^2+x1^2·x2^3-x1^2-x2^2)となり、最初のψ(0)に一致することがわかり、基本対称式で正しく表現されていることが確認できる。このように、ウェアリングの方法を使うと、対称式を機械的な計算により、基本対称式の多項式に分解することができる。
※ 差し引くgの構成は、ある種の逐次近似的な考えからの発想か?
この節では、ウェアリングの方法を非対称型道中双六の平均日数の計算に適用してみます。
c=4では、s=2、固有値の2乗をxと記載した固有方程式は、
φ(x)=x^2+x·(2·p^2-p-1)+p·(p^2-2·p+1)=0、である。
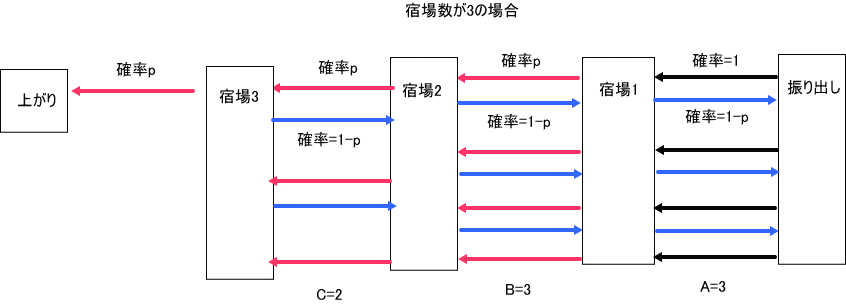
状態ベクトルは、[振り出し,宿場1,宿場2,宿場3]までで、要素数は、4。(宿場3が最後の宿場)
初期状態は、U0=([1,0,0,0]`)、ただし、転置をつけて縦ベクトルとしています。
一方、U4(3)等は、U4(3)=(A^3U)↓4、から求められるが、Aは、下図の通りなので、
U4(3)=p^2≡u3、
U4(5)=p^2(1-p)(2p+1)≡u5、などと略記します。
第90回で非対称型道中双六の上がりまでの平均日数の計算について、次の公式が得られています。
ここで、c=宿場数+1、pを推移確率として、cが偶数の場合は、c=2s、ただし、s=1、2、3・・として、
上図の上段は、c=2s、の一般の偶数の場合、下段がs=2の場合です。
なお、係数diは、次の2つの関係式から求めることができる。
m=0~s-1、のs個を動きます。
Ucは、[U1(t),U2(t),・・,U2s(t)]と書ける状態ベクトル。
1が振り出しを、c=2sが上がり直前の最後の宿場を表す。
上図の上段は、c=2s、の一般の偶数の場合、下段がs=2の場合です。
d1等は、上の図の2段目に示した2元連立方程式を解くことにより、求められる。
d1=(u3·x2-u5)/(x2-x1)、
d2=(u3·x1-u5)/(x1-x2))、となる。
d1、d2を平均日数の公式に代入すると、平均日数=2p×Ψ/p^6、と書けることが分かる。
後述するように、分母は、固有方程式をφ(x)としたとき、分母=φ(1)^2、となるので、容易に計算できる。
Ψは、
ψ=(-u3·x1^2·x2+2·u3·x1^2-u3·x1·x2^2+x1·x2·(4·u3+u5)-2·x1·(2·u3+u5)+2·u3·x2^2-x2·(4·u3+2·u5)+2·u3+3·u5)、となる。
そこで、
ψ(0)=(-u3·x1^2·x2+2·u3·x1^2-u3·x1·x2^2+x1·x2·(4·u3+u5)-2·x1·(2·u3+u5)+2·u3·x2^2-x2·(4·u3+2·u5)+2·u3+3·u5)
とおいて、ウェアリングの方法により、基本対称式で表してみよう。
ψ(0)の最大次数は、第1項で、(2,1)、係数は、-u3、
引き去るg(1)=-u3s1^(2-1)s2^1
ψ(1)=Ψ(0)-g(1)=(2·u3·x1^2+x1·x2·(4·u3+u5)-x1·(4·u3+2·u5)+2·u3·x2^2-x2·(4·u3+2·u5)+2·u3+3·u5)、
以下同様に、ψ(1)の最大次数は、第1項で、(2,0)、係数は、2u3、
g(2)=2u3s1^2s2^0=2u3s1^2
ψ(2)=(u5·x1·x2-x1·(4·u3+2·u5)-2·x2·(2·u3+u5)+2·u3+3·u5)
ψ(2)の最大次数は、第1項で、(1,1)、係数は、u5、
g(3)=u5×s1^(1-1)s2^1
ψ(3)=(-2·x1·(2·u3+u5)-2·x2·(2·u3+u5)+2·u3+3·u5)
ψ(3)の最大次数は、第1項で、(1,0)、係数は、-2·(2·u3+u5)、
g(4)=-2·(2·u3+u5)s1^1s2^0
ψ(5)=(2·u3+3·u5)、これは、定数である。
従って、ψ(0)=(2·u3+3·u5)+(-2·(2·u3+u5)s1^1)+(u5s2)+(2u3s1^2)+(-u3s1s2)
=(2·s1^2·u3-s1·(s2·u3+2·(2·u3+u5))+s2·u5+2·u3+3·u5)
検算すると、元のψ(0)に等しいことが分かる。
道中双六の問題のパラメーターを使えば、
s1=x1+x2=-a1、s2=x1x2=a0、であるから、
ψ(0)=(u3·(a0·a1+2·(a1^2+2·a1+1))+u5·(a0+2·a1+3))
a1=(2·p^2-p-1)、
※ a1は、方程式、φ(x)=x^2+x·(2·p^2-p-1)+p·(p^2-2·p+1)=0、の1次項の係数。
うっかりと、余分な負号を追加しないように!。
a0=p·(p-1)^2、u3=p^2、u5=p^2(1-p)(2p+1)、を代入すると、
ψ(0)=(p^2·(2·p^2-p+1))
よって、
平均日数=2ψ(0)/p^5
=2·(2·p^2-p+1)/p^3、となり、
これまで得ていた結果と一致する。
c=6では、s=3、固有値の2乗をxと記載すると、方程式は、
φ(x)=x^3+x^2·(4·p^2-3·p-1)+x3·p·(p+1)·(p-1)^2+p^2·(p-1)^3、である。
一方、U6(5)等は、
から求められるが、Aは、下図の通りなので、
U6(5)=p^4
U6(7)=p^4·q·(4·p+1)=p^4·(1-p)·(4·p+1)
U6(9)=p^4·(p-1)^2·(13·p^2+5·p+1)となる。
以下、U6(5)等は、u5等と記載する。
また、方程式の係数をa0~a2と略記すると、
φ(x)=x^3+x^2·(4·p^2-3·p-1)+x3·p·(p+1)·(p-1)^2+p^2·(p-1)^3
=x^3+a2x^2+a1x+a0、であり、
a0=-p^2·(1-p)^3
a1=3·p·(p+1)·(1-p)^2
a2=-(1-p)(4p+1)
である。
c=4の場合と同様に平均日数の式を展開すると、c=6の場合の平均日数の分母は、p^10となる。
これは、(φ(1))^2から、直接、計算して確かめられる。
次に、分子は、ψ(x1,x2,x3)=Σdk(3-2xk)(1-xk+1)^2(1-xk+2)^2、
ここで、下添え字kは、3を法として、1から3まで動くものとする。
平均日数=2×ψ/p^9、である。
(分子の2pの因子と分母のp^10を勘案)
さて、基本対称式は、
s1=x1+x2+x3
s2=x1x2+x1x3+x2·x3
s3=x1·x2·x3、の3つである。
3次方程式の根と係数の関係から、
a0=-x1·x2·x3
a1=(x1x2+x1x3+x2·x3)
a2=-(x1+x2+x3)、でもある。
平均日数=2×ψ/p^9、であるので、
分子のψは、ψ=(d1·(3-2·x1)·(1-x2)^2·(1-x3)^2+d2·(3-2·x2)·(1-x1)^2·(1-x3)^2+d3·(3-2·x3)·(1-x1)^2·(1-x2)^2)、
となる
3元連立方程式、([1,1,1;x1,x2,x3;x1^2,x2^2,x3^2]·[d1,d2,d3]`=[u5,u7,u9]`)、を解けば、
d1=(u5·x2·x3-u7·(x2+x3)+u9)/((x1-x2)·(x1-x3))
d2=(u5·x1·x3-u7·(x1+x3)+u9)/((x1-x2)·(x3-x2))
d3=(u5·x1·x2-u7·(x1+x2)+u9)/((x1-x3)·(x2-x3))、
と求められる。
これらから、ψ(0)は、
ψ(0)=-2·u5·x1^2·x2^2·x3+3·u5·x1^2·x2^2-2·u5·x1^2·x2·x3^2+x1^2·x2·x3·(7·u5+2·u7)-3·x1^2·x2·(2·u5+u7)+3·u5·x1^2·x3^2-x1^2·x3·(6·u5+3·u7)+x1^2·(3·u5+4·u7)-2·u5·x1·x2^2·x3^2+x1·x2^2·x3·(7·u5+2·u7)-3·x1·x2^2·(2·u5+u7)+x1·x2·x3^2·(7·u5+2·u7)-x1·x2·x3·(18·u5+10·u7+2·u9)+x1·x2·(12·u5+10·u7+3·u9)-x1·x3^2·(6·u5+3·u7)+x1·x3·(12·u5+10·u7+3·u9)-x1·(6·u5+8·u7+4·u9)+3·u5·x2^2·x3^2-x2^2·x3·(6·u5+3·u7)+x2^2·(3·u5+4·u7)-3·x2·x3^2·(2·u5+u7)+x2·x3·(12·u5+10·u7+3·u9)-x2·(6·u5+8·u7+4·u9)+x3^2·(3·u5+4·u7)-2·x3·(3·u5+2·(2·u7+u9))+3·u5+4·u7+5·u9、となる。
赤く色を付けた第1項がΨ(0)の最大次数の単項式である。
Ψ(0)をウェアリングの方法により、基本対称式に置き換えていく。
最大次数:(2,2,1)、係数:-2u5
g(1)=-2u5s1^(2-2)s2^(2-1)s3^1、
Ψ(1)=Ψ(0)-g(1)=(3·u5·x1^2·x2^2+x1^2·x2·x3·(7·u5+2·u7)-x1^2·x2·(6·u5+3·u7)+3·u5·x1^2·x3^2-x1^2·x3·(6·u5+3·u7)+x1^2·(3·u5+4·u7)+x1·x2^2·x3·(7·u5+2·u7)-x1·x2^2·(6·u5+3·u7)+x1·x2·x3^2·(7·u5+2·u7)-x1·x2·x3·(18·u5+10·u7+2·u9)+x1·x2·(12·u5+10·u7+3·u9)-3·x1·x3^2·(2·u5+u7)+x1·x3·(12·u5+10·u7+3·u9)-x1·(6·u5+8·u7+4·u9)+3·u5·x2^2·x3^2-x2^2·x3·(6·u5+3·u7)+x2^2·(3·u5+4·u7)-3·x2·x3^2·(2·u5+u7)+x2·x3·(12·u5+10·u7+3·u9)-x2·(6·u5+8·u7+4·u9)+x3^2·(3·u5+4·u7)-2·x3·(3·u5+2·(2·u7+u9))+3·u5+4·u7+5·u9)
最大次数:(2,2,0)、係数:3u5
g(2)=3u5s1^(2-2)s2^(2-0)s3^0=3u5s2^2
Ψ(2)=(x1^2·x2·x3·(u5+2·u7)-x1^2·x2·(6·u5+3·u7)-3·x1^2·x3·(2·u5+u7)+x1^2·(3·u5+4·u7)+x1·x2^2·x3·(u5+2·u7)-x1·x2^2·(6·u5+3·u7)+x1·x2·x3^2·(u5+2·u7)-x1·x2·x3·(18·u5+10·u7+2·u9)+x1·x2·(12·u5+10·u7+3·u9)-3·x1·x3^2·(2·u5+u7)+x1·x3·(12·u5+10·u7+3·u9)-x1·(6·u5+8·u7+4·u9)-3·x2^2·x3·(2·u5+u7)+x2^2·(3·u5+4·u7)-3·x2·x3^2·(2·u5+u7)+x2·x3·(12·u5+10·u7+3·u9)-x2·(6·u5+8·u7+4·u9)+x3^2·(3·u5+4·u7)-2·x3·(3·u5+2·(2·u7+u9))+3·u5+4·u7+5·u9)
最大次数:(2,1,1)、係数:(u5+2·u7)
g(3)=(u5+2·u7)s1^(2-1)s2^(1-1)s3^1=(u5+2·u7)s1s3
Ψ(3)=(-3·x1^2·x2·(2·u5+u7)-3·x1^2·x3·(2·u5+u7)+x1^2·(3·u5+4·u7)-3·x1·x2^2·(2·u5+u7)-2·x1·x2·x3·(9·u5+5·u7+u9)+x1·x2·(12·u5+10·u7+3·u9)-3·x1·x3^2·(2·u5+u7)+x1·x3·(12·u5+10·u7+3·u9)-x1·(6·u5+8·u7+4·u9)-3·x2^2·x3·(2·u5+u7)+x2^2·(3·u5+4·u7)-3·x2·x3^2·(2·u5+u7)+x2·x3·(12·u5+10·u7+3·u9)-x2·(6·u5+8·u7+4·u9)+x3^2·(3·u5+4·u7)-2·x3·(3·u5+2·(2·u7+u9))+3·u5+4·u7+5·u9)
最大次数:(2,1,0)、係数:-3(2·u5+u7)
g(4)=-3(2·u5+u7)s1^(2-1)s2^(1-0)s3^0=-3(2·u5+u7)s1s2
Ψ(4)=(x1^2·(3·u5+4·u7)-x1·x2·x3·(u7+2·u9)+x1·x2·(12·u5+10·u7+3·u9)+x1·x3·(12·u5+10·u7+3·u9)-2·x1·(3·u5+2·(2·u7+u9))+x2^2·(3·u5+4·u7)+x2·x3·(12·u5+10·u7+3·u9)-2·x2·(3·u5+2·(2·u7+u9))+x3^2·(3·u5+4·u7)-2·x3·(3·u5+2·(2·u7+u9))+3·u5+4·u7+5·u9)
最大次数:(2,0,0)、係数:(3·u5+4·u7)
g(5)=(3·u5+4·u7)s1^2
Ψ(5)=(-x1·x2·x3·(u7+2·u9)+x1·x2·(6·u5+2·u7+3·u9)+x1·x3·(6·u5+2·u7+3·u9)-2·x1·(3·u5+2·(2·u7+u9))+x2·x3·(6·u5+2·u7+3·u9)-2·x2·(3·u5+2·(2·u7+u9))-2·x3·(3·u5+2·(2·u7+u9))+3·u5+4·u7+5·u9)
最大次数:(1,1,1)、係数:-(u7+2·u9)
g(6)=-(u7+2·u9)s1^0s2^0s3^1=-(u7+2·u9)s3
Ψ(6)=(x1·x2·(6·u5+2·u7+3·u9)+x1·x3·(6·u5+2·u7+3·u9)-2·x1·(3·u5+2·(2·u7+u9))+x2·x3·(6·u5+2·u7+3·u9)-2·x2·(3·u5+2·(2·u7+u9))-2·x3·(3·u5+2·(2·u7+u9))+3·u5+4·u7+5·u9)
最大次数:(1,1,0)、係数:(6·u5+2·u7+3·u9)
g(7)=(6·u5+2·u7+3·u9)s1^0s2^1s3^0=(6·u5+2·u7+3·u9)s2
Ψ(7)=(-2·x1·(3·u5+2·(2·u7+u9))-2·x2·(3·u5+2·(2·u7+u9))-2·x3·(3·u5+2·(2·u7+u9))+3·u5+4·u7+5·u9)
最大次数:(1,0,0)、係数:-2·(3·u5+2·(2·u7+u9))
g(8)=-2·(3·u5+2·(2·u7+u9))s1
Ψ(8)=(3·u5+4·u7+5·u9)、
これは、定数なので、あとは、これにg(1)~g(8)を加えていく。
Ψ(0)=(3·u5+4·u7+5·u9)+-2·(3·u5+2·(2·u7+u9))·s1+(6·u5+2·u7+3·u9)·s2+-(u7+2·u9)·s3+(3·u5+4·u7)·s1^2+-3·(2·u5+u7)·s1·s2+(u5+2·u7)·s1·s3+3·u5·s2^2+-2·u5·s1^(2-2)·s2^(2-1)·s3^1
=(u5·(3·s1^2-s1·(6·s2-s3+6)+3·s2^2+2·s2·(3-s3)+3)+u7·(4·s1^2+s1·(2·(s3-4)-3·s2)+2·s2-s3+4)-u9·(4·s1-3·s2+2·s3-5))
検算のため、s1等をx1等で表し、元のΨから引き算すると、
元のΨ-(-u5·(x1^2·(x2^2·(2·x3-3)+x2·(2·x3^2-7·x3+6)-3·x3^2+6·x3-3)+x1·(x2^2·(2·x3^2-7·x3+6)-x2·(7·x3^2-18·x3+12)+6·(x3^2-2·x3+1))-3·(x2^2·(x3^2-2·x3+1)-2·x2·(x3^2-2·x3+1)+x3^2-2·x3+1))+u7·(x1^2·(x2·(2·x3-3)-3·x3+4)+x1·(x2^2·(2·x3-3)+x2·(2·x3^2-10·x3+10)-3·x3^2+10·x3-8)+x2^2·(4-3·x3)-x2·(3·x3^2-10·x3+8)+4·(x3^2-2·x3+1))-u9·(x1·(x2·(2·x3-3)-3·x3+4)+x2·(4-3·x3)+4·x3-5))=0、となることで、正しいことが確かめられる。
道中双六の平均日数の計算に必要な、パラメーターを整理すると、pの関数として、次の表となる。
道中双六の平均日数は、上の表に従い、s1等をpの式で置き換えて、
Ψ(0)=(p^4·(3·p^4-3·p^3+5·p^2-3·p+1))、となることで、
平均日数=2Ψ(0)/p^9=2·(3·p^4-3·p^3+5·p^2-3·p+1)/p^5、
となり、以前に求めた値と等しいことが分かる。
宿場数が7の場合であり、s=4となるので、DERIVEで4次方程式の厳密解が得られるが、方程式の係数が数でないと平均日数の計算途中で難しいケースである。固有値の2乗をxとした固有方程式は、
φ(x)=x^4+x^3·(6·p^2-5·p-1)+5·p·x^2·(p-1)^2·(2·p+1)+2·p^2·x·(p-1)^3·(2·p+3)+p^3·(p-1)^4、である。
一方、U8(7)等は、Uc(k)=(A^kU)c、から求められる。
Aは、下図の通りなので、
U8(7)=p^6·
U8(9)=p^6·(1-p)·(6·p+1)
U8(11)=p^6·(p-1)^2·(26·p^2+7·p+1)
U8(13)=p^6·(1-p)^3·(100·p^3+34·p^2+8·p+1)
以下、U8(7)等は、u7等と記載する。
また、固有方程式の係数をa0~a3と略記すると、
φ(x)=x^4+a3x^3+a2x^2+a1x+a0、
a0=p^3·(p-1)^4
a1=2·p^2·(p-1)^3·(2·p+3)
a2=5·p·(p-1)^2·(2·p+1)
a3=6·p^2-5·p-1
である。
c=6の場合と同様に平均日数の式を展開すると、
c=8の場合の平均日数の分母は、後述するように、p^2(c-1)=p^14となる。これは、(φ(1))^2から、直接、計算しても確かめられる。
次にψ(x1,x2,x3,x4)=Σdk(4-3xk)(1-xk+1)^2(1-xk+2)^2(1-xk+3)^2
ここで、下添え字kは、4を法として、1から4まで動くものとする。
平均日数=2×ψ/p^13、である。
(分子の2pの因子と分母のp^14を勘案)
4次方程式φ(x)=0、の根と係数の関係は、
3次項の係数=a3=-(x1+x2+x3+x4)、
2次項の係数=a2=(x1·x2+x1·x3+x1·x4+x2·x3+x2·x4+x3·x4)、
1次項の係数=a1=-(x1·x2·x3+x1·x2·x4+x1·x3·x4+x2·x3·x4)、
定数項=a0=(x1·x2·x3·x4)
これをd1~d4に対する連立方程式と見て、d1等を解くと、
d1=(u11·(x2+x3+x4)-u13+u7·x2·x3·x4-u9·(x2·(x3+x4)+x3·x4))/((x1-x2)·(x1-x3)·(x4-x1))
d2=(u11·(x1+x3+x4)-u13+u7·x1·x3·x4-u9·(x1·(x3+x4)+x3·x4))/((x1-x2)·(x2-x3)·(x2-x4))
d3=(u11·(x1+x2+x4)-u13+u7·x1·x2·x4-u9·(x1·(x2+x4)+x2·x4))/((x1-x3)·(x2-x3)·(x4-x3))
d4=(u11·(x1+x2+x3)-u13+u7·x1·x2·x3-u9·(x1·(x2+x3)+x2·x3))/((x1-x4)·(x2-x4)·(x3-x4)))
となる。
次にψを具体的に書き下ろす。
ψ(x1,x2,x3,x4)=Σdk(4-3xk)(1-xk+1)^2(1-xk+2)^2(1-xk+3)^2、である。
これを使うと、平均日数=2×ψ/p^13、と書ける。
Ψ(0)=(-3·u7·x1^2·x2^2·x3^2·x4+4·u7·x1^2·x2^2·x3^2-3·u7·x1^2·x2^2·x3·x4^2+x1^2·x2^2·x3·x4·(10·u7+3·u9)-4·x1^2·x2^2·x3·(2·u7+u9)+4·u7·x1^2·x2^2·x4^2-4·x1^2·x2^2·x4·(2·u7+u9)+x1^2·x2^2·(4·u7+5·u9)-3·u7·x1^2·x2·x3^2·x4^2+x1^2·x2·x3^2·x4·(10·u7+3·u9)-4·x1^2·x2·x3^2·(2·u7+u9)+x1^2·x2·x3·x4^2·(10·u7+3·u9)-x1^2·x2·x3·x4·(3·u11+25·u7+14·u9)+x1^2·x2·x3·(4·u11+16·u7+13·u9)-4·x1^2·x2·x4^2·(2·u7+u9)+x1^2·x2·x4·(4·u11+16·u7+13·u9)-x1^2·x2·(5·u11+8·u7+10·u9)+4·u7·x1^2·x3^2·x4^2-4·x1^2·x3^2·x4·(2·u7+u9)+x1^2·x3^2·(4·u7+5·u9)-4·x1^2·x3·x4^2·(2·u7+u9)+x1^2·x3·x4·(4·u11+16·u7+13·u9)-x1^2·x3·(5·u11+8·u7+10·u9)+x1^2·x4^2·(4·u7+5·u9)-x1^2·x4·(5·u11+8·u7+10·u9)+x1^2·(6·u11+4·u7+5·u9)-3·u7·x1·x2^2·x3^2·x4^2+x1·x2^2·x3^2·x4·(10·u7+3·u9)-4·x1·x2^2·x3^2·(2·u7+u9)+x1·x2^2·x3·x4^2·(10·u7+3·u9)-x1·x2^2·x3·x4·(3·u11+25·u7+14·u9)+x1·x2^2·x3·(4·u11+16·u7+13·u9)-4·x1·x2^2·x4^2·(2·u7+u9)+x1·x2^2·x4·(4·u11+16·u7+13·u9)-x1·x2^2·(5·u11+8·u7+10·u9)+x1·x2·x3^2·x4^2·(10·u7+3·u9)-x1·x2·x3^2·x4·(3·u11+25·u7+14·u9)+x1·x2·x3^2·(4·u11+16·u7+13·u9)-x1·x2·x3·x4^2·(3·u11+25·u7+14·u9)+x1·x2·x3·x4·(18·u11+3·u13+56·u7+43·u9)-2·x1·x2·x3·(9·u11+2·(u13+8·(u7+u9)))+x1·x2·x4^2·(4·u11+16·u7+13·u9)-2·x1·x2·x4·(9·u11+2·(u13+8·(u7+u9)))+x1·x2·(16·u11+5·u13+16·u7+20·u9)-4·x1·x3^2·x4^2·(2·u7+u9)+x1·x3^2·x4·(4·u11+16·u7+13·u9)-x1·x3^2·(5·u11+8·u7+10·u9)+x1·x3·x4^2·(4·u11+16·u7+13·u9)-2·x1·x3·x4·(9·u11+2·(u13+8·(u7+u9)))+x1·x3·(16·u11+5·u13+16·u7+20·u9)-x1·x4^2·(5·u11+8·u7+10·u9)+x1·x4·(16·u11+5·u13+16·u7+20·u9)-2·x1·(6·u11+3·u13+4·u7+5·u9)+4·u7·x2^2·x3^2·x4^2-4·x2^2·x3^2·x4·(2·u7+u9)+x2^2·x3^2·(4·u7+5·u9)-4·x2^2·x3·x4^2·(2·u7+u9)+x2^2·x3·x4·(4·u11+16·u7+13·u9)-x2^2·x3·(5·u11+8·u7+10·u9)+x2^2·x4^2·(4·u7+5·u9)-x2^2·x4·(5·u11+8·u7+10·u9)+x2^2·(6·u11+4·u7+5·u9)-4·x2·x3^2·x4^2·(2·u7+u9)+x2·x3^2·x4·(4·u11+16·u7+13·u9)-x2·x3^2·(5·u11+8·u7+10·u9)+x2·x3·x4^2·(4·u11+16·u7+13·u9)-2·x2·x3·x4·(9·u11+2·(u13+8·(u7+u9)))+x2·x3·(16·u11+5·u13+16·u7+20·u9)-x2·x4^2·(5·u11+8·u7+10·u9)+x2·x4·(16·u11+5·u13+16·u7+20·u9)-2·x2·(6·u11+3·u13+4·u7+5·u9)+x3^2·x4^2·(4·u7+5·u9)-x3^2·x4·(5·u11+8·u7+10·u9)+x3^2·(6·u11+4·u7+5·u9)-x3·x4^2·(5·u11+8·u7+10·u9)+x3·x4·(16·u11+5·u13+16·u7+20·u9)-2·x3·(6·u11+3·u13+4·u7+5·u9)+x4^2·(6·u11+4·u7+5·u9)-2·x4·(6·u11+3·u13+4·u7+5·u9)+6·u11+7·u13+4·u7+5·u9)
あまりに長いので、読者の皆さまは、さぞ、驚かれたでしょう。申し訳ございません。
以下、gは、書きますが、長くなるため、Ψは、省略します。
Ψ(0)から引き去るg(1)は、
g(1)=-3·s3·s4·u7、
あとは、途中のΨは、省略し、gのみを記載していきます。
g(2)=4·s3^2·u7、
g(3)=s2·s4·(2·u7+3·u9)、
g(4)=-4·s2·s3·(2·u7+u9)、
g(5)=s2^2·(4·u7+5·u9)、
g(6)=-s1·s4·(3·u11+u7+2·u9)、
g(7)=s1·s3·(4·u11+8·u7+3·u9)、
g(8)=-s1·s2·(5·u11+8·u7+10·u9)、
g(9)=s1^2·(6·u11+4·u7+5·u9)、
g(10)=s4·(2·u11+3·u13+u9)、
g(11)=-s3·(3·u11+2·(2·u13+4·u7+u9))、
g(12)=s2·(4·u11+5·u13+2·(4·u7+5·u9))、
g(13)=-2·s1·(6·u11+3·u13+4·u7+5·u9)、
残差=(6·u11+7·u13+4·u7+5·u9)、これは、定数なので繰り返し計算終了。
そこで、元のΨを基本対称式であらわすと
Ψ(0)=(6·u11+7·u13+4·u7+5·u9)+g(1)+~+g(13)から、
=(u9·(5·s1^2-s1·(10·s2-3·s3+2·(s4+5))+5·s2^2-s2·(4·s3-3·s4-10)-2·s3+s4+5)+u7·(4·s1^2-s1·(8·s2-8·s3+s4+8)+4·s2^2-2·s2·(4·s3-s4-4)+4·s3^2-s3·(3·s4+8)+4)-u13·(6·s1-5·s2+4·s3-3·s4-7)+u11·(6·s1^2-s1·(5·s2-4·s3+3·(s4+4))+4·s2-3·s3+2·(s4+3)))となった。
検算して、元のΨと一致することを確かめた。
一方、Ψのs1等を固有方程式の係数と、u9等を具体的なpの関数に置き換える。
すでに記載した内容の一部と重複しますが、
方程式は、
φ(x)=x^4+x^3·(6·p^2-5·p-1)+5·p·x^2·(p-1)^2·(2·p+1)+2·p^2·x·(p-1)^3·(2·p+3)+p^3·(p-1)^4
基本対称式は、
3次項:a3=-(x1+x2+x3+x4)=-s1、
2次項:a2=(x1·x2+x1·x3+x1·x4+x2·x3+x2·x4+x3·x4)=s2、
1次項:a1=-(x1·x2·x3+x1·x2·x4+x1·x3·x4+x2·x3·x4)=-s3、
定数項:a0=(x1·x2·x3·x4)=s4
方程式の係数は、
a0=p^3·(p-1)^4
a1=2·p^2·(p-1)^3·(2·p+3)
a2=5·p·(p-1)^2·(2·p+1)
a3=6·p^2-5·p-1
状態ベクトルのt=7~13までの値は、
u7=p^6·
u9=p^6·(1-p)·(6·p+1)
u11=p^6·(p-1)^2·(26·p^2+7·p+1)
u13=p^6·(1-p)^3·(100·p^3+34·p^2+8·p+1)、となっている。
よって、平均日数の分子のΨは、
Ψ=(p^6·(4·p^6-6·p^5+14·p^4-16·p^3+12·p^2-5·p+1))、となる。
これから、平均日数は、
平均日数=2pΨ/p^14=2·(4·p^6-6·p^5+14·p^4-16·p^3+12·p^2-5·p+1)/p^7
以前に平均日数を数値計算して、推定した平均日数を再掲すれば、
2(4p^6-6p^5+14p^4-16p^3+12p^2-5p+1)/p^7、となっていたので、
これまでの数値計算の結果と一致し、以前の推定式が厳密に正しいことが裏付けられた。
宿場数が9の場合は、s=5となるため、これまで、平均日数の公式での厳密解は、求めてきませんでした。第88回の『マルコフ過程(1)(非対称型道中双六:宿場数=3~9)』では、平均日数公式とは、別の表し方による式で数値計算を行い、更に、cが10より小さい場合の平均日数の式をもとに、pの有理式の係数を推定したものです。
それが、平均日数=2(5p^8-10p^7+30p^6-50p^5+58p^4-45p^3+23p^2-7p+1)/p^9、(推定式)です。
では、c=8までの例にならって、計算を行います。その方法は、同様ですので、必要なデータのみを列記することとします。
推移確率行列A
固有方程式(ただし、固有値の2乗をxと書き換えた方程式)
φ(x)≔x^5+x^4·(8·p^2-7·p-1)+7·p·x^3·(3·p^3-5·p^2+p+1)+5·p^2·x^2·(p-1)·(4·p^3-5·p^2-2·p+3)+5·p^3·x·(p+2)·(p-1)^4+p^4·(p-1)^5、
平均日数の分子(2pを除いた)Ψ、
Ψ=(d1·(5-4·x1)·(1-x2)^2·(1-x3)^2·(1-x4)^2·(1-x5)^2+d2·(5-4·x2)·(1-x1)^2·(1-x3)^2·(1-x4)^2·(1-x5)^2+d3·(5-4·x3)·(1-x1)^2·(1-x2)^2·(1-x4)^2·(1-x5)^2+d4·(5-4·x4)·(1-x1)^2·(1-x2)^2·(1-x3)^2·(1-x5)^2+d5·(5-4·x5)·(1-x1)^2·(1-x2)^2·(1-x3)^2·(1-x4)^2)、
Ψのd1等と状態ベクトルとの関係式
右辺のu9等は、状態ベクトルの10番目の要素の時刻9等の際の値。
状態ベクトル
初期状態は、U0=[1,0,0,0,0,0,0,0,0,0]`
vu9≔(LIM(A^9·u0,q,1-p))↓10=p^8、などと求められる。(q=1-p)
これらを元にすると、平均日数=2p×Ψ/p^(2(10-1))=2Ψ/p^17、である。ここで、d1等を代入して整理した結果、Ψは、ものすごく長い式となるため、ここでは省略します。ウェアリングの方法により、基本対称式に分解していく作業を後述するDERIVEのユーザー定義関数を使って行いますと、19回目で残差が定数となりました。
([19,-2·s1·(6·u11+7·u13+8·u15+4·u17+5·u9),6·u11+7·u13+8·u15+9·u17+5·u9])
赤字の式が定数。
ここから、元のΨを基本対称式のみで表しますと、
Ψ=(s1^2·(6·u11+7·u13+8·u15+5·u9)-s1·(s2·(12·u11+14·u13+7·u15+10·u9)-s3·(12·u11+5·u13+2·(3·u15+5·u9))+s4·(3·u11+4·u13+5·(u15+2·u9))-s5·(2·u11+3·u13+4·u15+u9)+2·(6·u11+7·u13+8·u15+4·u17+5·u9))+s2^2·(6·u11+7·u13+5·u9)-s2·(2·s3·(6·u11+3·u13+5·u9)-s4·(4·u11+5·(u13+2·u9))+s5·(3·u11+2·(2·u13+u9))-12·u11-14·u13-6·u15-7·u17-10·u9)+s3^2·(6·u11+5·u9)-s3·(5·s4·(u11+2·u9)-s5·(4·u11+3·u9)+12·u11+4·u13+5·u15+2·(3·u17+5·u9))+5·s4^2·u9-s4·(4·s5·u9-2·u11-3·u13-4·u15-5·(u17+2·u9))-s5·(u11+2·u13+3·u15+4·u17)+6·u11+7·u13+8·u15+9·u17+5·u9)、
と分解されました。
平均日数をpの関数として表すために、Ψのs1等をφ(x)の係数(符号を考慮して)、置き換えます。具体的には、
s1=-a4
s2=a3
s3=-a2
s4=a1
s5=-a0、
ここで、a4等は、φ(x)の4次項等の係数です。
また、状態ベクトルの値は、
u9=p^8
u11=(p^8·(1-p)·(8·p+1))
u13=(p^8·(p-1)^2·(43·p^2+9·p+1))
u15=(p^8·(1-p)^3·(196·p^3+53·p^2+10·p+1))
u17=(p^8·(p-1)^4·(820·p^4+260·p^3+64·p^2+11·p+1))
Ψ=(p^8·(5·p^8-10·p^7+30·p^6-50·p^5+58·p^4-45·p^3+23·p^2-7·p+1))
よって、
平均日数=2Ψ/p^17
=2·(5·p^8-10·p^7+30·p^6-50·p^5+58·p^4-45·p^3+23·p^2-7·p+1)/p^9、となりました。
これは、第88回における推定式と一致しました。
※ 「Ψの式がx1等で表した場合よりも基本対称式で表した方が項数が少なくなる一因は?」に錯誤がありましたので、全文を削除しました。2019/8/24
この節がないと、いけないので、少し補足します。平均日数公式には、以下のように、xiとdiが含まれています。
下の図は、c=2sとしたときs=2の例。
この式のままであれば、たとえば、x1とx2を交換するとき、
仮に、d1、d2、が入れ替わらないとすると、右辺の和は、変わる。
しかし、di等は、以下でx1等と結びついているので、
x1とx2が交換されると、d1は、d1'、d2は、d2'と変わるとすれば、
d1'+d2'=U4(3)
x2d1'+x1d2'=U4(5)、である。
第2式の項の順番を変えれば、
x1d2'+x2d1'=U4(5)となる。
任意のx1等に対して、2つの式が成り立つことから、d2'=d1、d1'=d2、であることが分かる。
sが3以上の場合も、d1等をクラメルの公式を使って表せば、上の事柄は、ほぼ、自明となる。
また、cが奇数(=2s+1、s=1、2,・・)の場合もほぼ同じである。
※上の図では、x1等の代わりにμ1等を使用しています。
このように、平均日数の公式は、任意の根の互換に対して、その値を変えないことから、対称式であることが分かりました。
付言すれば、d1等を決める連立方程式の左辺に現れる行列Dは、その行列式det(D)^2が方程式の『判別式』に符号を除いて等しい。
なお、このdet(D)は、Vandermonde(フォンデルモンド)の行列式と言われるものです。
以前にも注意していますが、平均日数公式のdi等を代入して、分母を一つにまとめた場合、
その分母は、Π(1-xi)^2、i=1~s、となります。
なお、cが奇数の場合、たとえば、c=5では、固有方程式は、5次となりますが、
それは、固有値×固有値の4次式、となるので、固有値の2乗をxとした方程式は、xの2次方程式となります。
一般には、c=2s+1としたとき、s次方程式です。
従って、分母については、Π(1-xi)^2、i=1~s、は、いずれの場合も成り立ちます。
この値は、φ(1)^2、です。
ここで、φ(x)は、固有方程式の根の2乗をxと置いたときの方程式です。
また、第92回の固有方程式の一般形の結果を使えば、φ(1)^2=p^2(c-1)、となることが分かります。
奇数の場合は、φ(1)^2=p^(2c-2)、となります。(赤字部分を訂正しました。2020/7/19)
※ 元の固有方程式(固有値λの2乗をxと置く以前のもの)は、w=√(λ^2-4p+4p^2)、として、cの偶奇に関わらず、
と与えられることが分かっています。(第92回)
※ λ^2=xとおいた新方程式でφ(x=1)を計算する際、元の方程式でλ=1として計算しても結果は、同じです。
c=2s、の場合、平均日数は、s=1,2、・・として、
平均日数=2pΣdi×(s-(s-1)xi)/(1-xi)^2、i=1~s、です。
また、c=2s+1、の場合は、s=1,2、・・として、
平均日数=Σdi×(2s+1-(2s-1)xi)/(1-xi)^2、i=1~s、です。
先に述べたように、いずれの場合においても、xiとxjを交換した場合、diもdjと交換となるため、平均日数の値は、変わりません。
これが、平均日数の式が対称式である理由でした。
一方、diの式は、di=DET(Bi)/DET(D)、のようにクラメルの公式で書くことができます。
分母のDは、前々節のとおり、判別式と符号を別にすれば、同一となり、具体的には、DET(D)=Π(xi-xj)、ただし、i>j、です。
これにより、平均日数の式は、前節の共通分母として出てくるΠ(1-xi)^2=(φ(1))^2、以外に、分母としてDET(D)も持つことになります。しかし、これまで、計算したs=2~5、のケースでは、DET(D)の部分は、分子部分の和と相殺されて、Ψの式には、現れません。それには、以下の理由があります。
cが4(s=2)を例にとり、丁寧に書くと、分子は、2pの因子を別にして、これまでのΨと区別して赤でΨと書けば、
Ψ=DET(B1)(2-x1)(1-x2)^2+DET(B2)(2-x2)(1-x1)^2、となります。
このとき、分母は、分母=(1-x1)^2(1-x2)^2×(x1-x2)=(φ(1))^2×(x2-x1)、であり、
ΨのDET(B1)=u3x2-u5、DET(B2)=u5-u3x1、となっています。
そうしますと、仮に、Ψをx1のみの関数と考えて、x1=x2と置きますと、
第1項=(u3x2-u5)(2-x1)(1-x2)^2⇒(u3x2-u5)(2-x2)(1-x2)^2、
第2項=(u5-u3x1)(2-x2)(1-x1)^2⇒(u5-u3x2)(2-x2)(1-x2)^2=-(u3x2-u5)(2-x2)(1-x2)^2、
となり、第1項+第2項=Ψ=0、となることが分かります。
これは、Ψが(x2-x1)の因子を持つことに他なりません。sが3以上の場合も同様です。
これにより、分母に元々あったDET(D)が消えて、分母は、(φ(1))^2、だけとなることが分かります。また、分子は、2pを除いて、元々のΨをDET(D)で除した式が、x1等の多項式、Ψとなります。これが、Ψがx1等の(分数式ではなく)多項式となる理由です。なお、cが奇数の場合も同様です。
変数が2つ、3つ程度でも、対称式を基本対称式に分解する作業を手計算で行うことは、単純とは言え面倒で、計算間違えから、とうてい逃れられません。最後に検算することは、もちろん、途中でも検算する必要があります。今回ほど、楽に計算を進めたいと感じたことはありません。そこで、『ウェアリングの方法』をDERIVEで行うための補助的な関数を作ってみました。なお、c=10の計算時、それまでのものに若干の追加、修正を行いました。
対称式と変数の個数を指定して、計算を実行して結果を待つだけというレベルには、至っていません。ステップ毎に以下の1~3の手作業が発生します。この理由は、DERIVEの多項式から、その第1項を抽出する方法が分からないためです。これがベクトルであれば、任意の要素を求める関数があるのですが、多項式について、項をマウスでクリックする以外の方法が不明なのです。DERIVEのヘルプをだいぶ探したのですが・・・。
0. Freset関数を実行して、作業ベクトル、更新回数等を初期状態にする、(計算開始時のみ)
1. Fg関数の実行後、表示される[更新回数,g,Ψ]から、Ψを次に実行するFg関数の第1引数とする、
2. Ψの第1項(これは最大次数)をFg関数の第2引数とする、
3. 第3引数に変数の個数を入れて計算を実行する、
手順の3の後、結果がゼロになれば、引き去ったgが記録されているベクトルvgの要素を1~更新回数まで加えることで、基本対称式で表されるΨを得ることができる。(本文では、定数になればと書いたが、Ψ=定数として、Fg関数をもう一回実行すれば、残差は、ゼロとなるので、この方法で良い)
準備として、DERIVEの白紙ページの冒頭で、
InputMode≔Word、を宣言して、変数を1文字以上の文字列として入力できるようにします。
通常は、オプションから指定するので、そうすれば、上のようにシートに表示されます。
次に、VariableOrder≔[x1,x2,x3,x4,x5,x6,x7,x8,x9,x10]、などと変数の並び替え順を指定する。これは、前述のように辞書式順序により、多項式を整理するために必要です。上では、10個までの変数の順序を設定しています。これも前述のように、オプションから指定する方が簡単でしょう。
変数名を入れるベクトルを用意します。
vx≔[x1,x2,x3,x4,x5,x6,x7,x8,x9,x10]
これは、大域変数として、使われます。(中身が変わることはありません。後述のFreset関数で中身をセットします)
基本対称式をx1等(vxの要素)で書き表して、入れておくベクトルvsも用意します。
また、vtは、vsの中身を計算するために利用する同次対称式を入れておくベクトルです。
vs≔[0,0,0,0,0,0,0,0,0,0]
vt≔[0,0,0,0,0,0,0,0,0,0]
基本対称式を表す変数を入れておくベクトルも用意する必要があります。
(中身が変わることはありません。後述のFreset関数で中身をセットします)
vss≔[s1,s2,s3,s4,s5,s6,s7,s8,s9,s10]、
※ 基本対称式をウィキのようにσ1、σ2、・・で表したいときは、ここを変更します。
また、変数の次数を入れるvaと基本対称式の各変数の次数、s1^(a1-a2)のような次数をvbで表します。
va≔[0,0,0,0,0,0,0,0,0,0]
vb≔[0,0,0,0,0,0,0,0,0,0]
これらのベクトルは、後述の補助関数Freset(n)で、定義して、変数の個数nに応じて、vtやvsは、値をセットします。
3つの補助関数を用意しました。
fs(m)≔
IF(m=1,vt↓1,(-1)^(m+1)·(1/m)·(vt↓m+∑((-1)^k·fs(k)·vt↓(m-k),k,1,m-1,1)))、
これは、ニュートンの多項式から、基本対称式を同次対称式で表すための関数です。
このfs(m)を使うと、
vs≔VECTOR(fs(m),m,1,n,1)、により、
nを与えて、nが3であれば、
vs=([x1+x2+x3,x1·(x2+x3)+x2·x3,x1·x2·x3])と、基本対称式がvsにセットされます。
後で述べる主関数Fg()の第2引数の単項式の変数の次数を数える補助関数、ban()です。
ban(f_,x_,n_)≔
PROG(
vw≔[0,0,0,0,0,0,0,0,0,0],
VECTOR(vw↓k_≔∂(f_,x_,k_),k_,1,n_+1,1),
b_≔0,
w_≔VECTOR(b_≔b_+IF(vw↓k_=0,0,1,1),k_,1,10,1),
b_
)
このままでは、なんだか意味不明な関数ですね。
ban(f_,x_,n_)は、第1引数の式を第2引数で偏微分して、f_の中に含まれるx_の次数を返します。
与えたn_+1まで、f_をx_で偏微分します。結果は、ベクトルとして、作業用のベクトルvwに格納します。
IF(vw↓k_=0,0,1,1)の4つ目の引数は、普通は、現れないものです。
IF関数が真偽不明の場合にここに記載の値を返します。
※ IF(式,真の場合の返り値,偽の場合の返り値,不明の場合の返り値)です。
真偽が決まる場合は、4つ目の引数は、省略します。
ban関数の働きをもう少し丁寧に述べます。
f_=x1^3x2^2x3、x_=x1のときを考えましょう。n=3では、
vw=[3x1^2x2^2x3,6x1x2x3,6x2x3,0,0,0,0,0,0]となります。
vwを1番目から見ていき、IF関数が1を返せば、作業用変数b_(作業用変数b_は、関数内で、最初にゼロとされる)に加えます。
すると上記の例では、b_は、3となります。これで、f_のx1の次数は、3であることが分かります。
IF関数で、真偽不明の場合も1が戻る仕組みとしているのは、DERIVEは、判定対象が『数』でない場合、たとえば、x1^2のように、(x1に値がセットされていなければ)、x1^2がゼロなのか?、と尋ねても、DERIVEとしては、真偽不明と返すしかないわけです。これは、数式処理ソフトとしては、当然ですが、そこに気がつくまで、すこし、時間が必要でした。
2019/8/18に追加した、リセット関数です。利用する作業用の変数やベクトルを初期化します。引数は、変数の個数です。計算をやり直したりする場合にも便利です。
Freset(n_)≔
PROG(
nn≔n_,
vs≔[0,0,0,0,0,0,0,0,0,0],
va≔[0,0,0,0,0,0,0,0,0,0],
vb≔[0,0,0,0,0,0,0,0,0,0],
vx≔[x1,x2,x3,x4,x5,x6,x7,x8,x9,x10],
vss≔[s1,s2,s3,s4,s5,s6,s7,s8,s9,s10],
kosin≔0,
vt≔[0,0,0,0,0,0,0,0,0,0],
vt≔VECTOR(∑(vx↓j^k,j,1,nn),k,1,nn,1),
vs≔VECTOR(fs(m),m,1,nn,1)
)
最後に主関数です。2019/8/18に、最後の行にExpand命令を追加して、Ψ等の出力結果を変数で展開して表示します。
Fg(ψ_,f_,n_)≔
PROG(
va≔VECTOR(ban(f_,vx↓j_,n_),j_,1,n_,1),
vb≔VECTOR(va↓j_-va↓(j_+1),j_,1,n_,1),vb↓n_≔va↓n_,
keisu_≔f_/∏(vx↓j_^va↓j_,j_,1,n_,1),
g_≔keisu_·∏(vss↓j_^vb↓j_,j_,1,n_,1),
w_≔LIM(ψ_-g_,vss↓1,vs↓1),
VECTOR(w_≔LIM(w_,vss↓j_,vs↓j_),j_,2,n_,1),
kosin≔kosin+1,
vg↓kosin≔g_,
EXPAND([kosin,g_,w_],Rational,x1,x2,x3,x4,x5,x6,x7,x8,x9,x10)
)
Fg(Ψ_,f_,n_)は、
第1引数=基本対称式に分解したい式を(F4キーで)コピーします。
第2引数=第1引数の式の第1項を(F4キーで)コピーします。
第3引数=変数の個数を直接入力します。
結果は、[更新回数,計算したg_,Ψ_からg_を引いた残差]がベクトルで表示されます。
なお、更新回数等を正しく出力するためには、Fgを初めて計算する前に、Freset関数を実行します。
Fgの3番目の要素がゼロになったならば、(Σvg↓j)、ただし、j=1~最後の更新回数、を計算することで、引き去ってきたg_を、シート上を探し回ることなく、簡単に集計することができます。
作成日2019/8/13、文字誤り等訂正2019/8/15、同8/16、
(4)に、c=10の節を追加し、Deriveのユーザー定義関数を修正、追加2019/8/18
(5)にΨが多項式となる理由追加2019/8/19、図をいくつか追加2019/8/20
文章の一部を加除修正2019/8/23、(4)の末尾の※の内容を削除2019/8/24
(3)の代数方程式小史に和算の算額や遺題継承を追記2019/8/26
(5)のユーザー定義関数の説明を加除訂正2019/8/27
(5)の「平均日数公式の分母」の1個所を訂正2020/7/19
小節に丸数字を追加、目次のリンクを短く:2020/9/17