「まったくよ。非対称道中双六の五十三次の平均日数を計算するための27変数27次対称式の基本対称式への分解は、できたの？」1.はじめに
2.フィボナッチ数列
（1）フィボナッチさん
（2）フィボナッチ数列の一般項
（3）フィボナッチ数列とマルコフ過程
（4）フィボナッチ数列の母関数
（5）初期値が異なるフィボナッチ数列
（6）一般のフィボナッチ数列
（7）トリボナッチ数列の一般項と対称式など
3.平均日数の計算に現れる級数
（1）非対称道中双六の平均日数
（2）c=4の計算過程で現れる級数
「2019年8月の第93回『マルコフ過程（6）（非対称型道中双六：平均日数と対称式）』以降、また、だいぶ、間が開いてしまったな」
「まったくよ。非対称道中双六の五十三次の平均日数を計算するための27変数27次対称式の基本対称式への分解は、できたの？」
「おう、ともちゃんかい。ご苦労さんじゃ。まだ、できておらん、と言うか、ま、正直にやるのは、無理じゃろうな。
しかし、2020年は、降って湧いたコロナ騒動で、なかなか、こちらに取りかかることができんかった。今思えば、2019年12月、のんきに謹賀新年などと年賀状を書いている場合ではなかったのう。謹賀新年どころか『難賀新年』、『虎狼泣観年』とでも書くべきであった。
もしや、『ノストラダムスの大予言』の1999年7月『炎の大王、天空より来たりて・・人類滅亡・・』は、今回のコロナ（corona=太陽の周囲の輝くガス）様の警告だったかもしれんなあ」
「なに、馬鹿なこと言っているの。ノストラだます、おっと、ダムスね。若い人は、ご存じないでしょ。それより今回、フィボナッチ数列を取り上げると言うけど、そもそも、道中双六と関係があるの？」
「おお、それは、コロナとノストラダムスより、深い関係があるじゃろう。
理由の一つは、普通のフィボナッチ数列は、2階の差分方程式で定義されるが、2次のマルコフ行列と状態ベクトルを使ったマルコフ過程と考えることもできる。道中双六の問題で、マルコフ過程の考え方を使うことにより、一般の宿場数の平均日数を計算する道筋が得られたように、フィボナッチ数列と道中双六との間に、『マルコフ過程』という大きな共通点があることが分かる。（青字個所を修正：2020/5/10）
二つ目は、フィボナッチ数列の一般項は、後述するように『ビネの公式』で表すことができる。このビネの公式と道中双六c=4の平均日数の計算に現れる級数（の閉じた表式）は、見た目が似ているんじゃ。
下図がフィボナッチ数列、f(n)で、初期値、f(0)＝f(1)＝1の場合の一般項を表すビネの公式だ。
一方、道中双六のc（宿場数+1）＝4に現れる級数の閉じた表式、fs(m,p)は、下のように求められる。
ここで、wは、下図の通り。
どうだ、似ておるじゃろうが」
「そいつは、道中双六で平均日数を計算する段階で、差分方程式を解くから、当然、似てくるんじゃないの？」
「いや、ともちゃんに答えを言われてしまったな。詳しくは、後述するが、直接には、まさに、その通りだな。
一方で、c（宿場数+1）が大きい場合の平均日数の計算式に表れる級数の閉じた値を求める手がかりが、フィボナッチ数列を取り上げる中で得られないか、という淡い期待もあるんじゃ」
「じゃ、早速、始めて下さいな」
目次へ戻る
「フィボナッチ数列は、イタリアの数学者、フィボナッチ（Fibonacchi：1180－1250）により、一つがいのウサギが次々と子供を作っていった場合の増え方から、彼が思いついたと言われている。ねずみ算ならぬ、うさぎ算とでも言うべきか。
ちなみに『フィボナッチ』は、岩波数学辞典第4版によると『ピサのレオナルド（通称フィボナッチ，1170頃～1240頃）は浩瀚（こうかん＝豊富な分量がある）な“算板の書”（1202，1228）で，アラビア数字による計算を含め最新のアラビア数学をラテン語で集大成した．その代数学の章（第15章）はその後ラテン世界で代数学の典拠となった．また“平方の書”（1225）では合同式を論じ，“精華” では3次方程式の解が平方根では扱えないことを理論的に論じ，また60進法で具体的に解を出している．・・』とある」
「へー。フィボナッチさんは、あだ名だったのか。でも、『ピサのレオナルド』のピサは、ピサの斜塔で有名なイタリアの都市『Pisa：イタリア中西部の都市。アルノ川河口に近い。中世、トスカーナ地方の門戸として東方貿易で繁栄したが、ジェノヴァに敗れ没落。斜塔や大聖堂、古来の大学などで有名。ガリレイの生地。：広辞苑第7版）』でしょう。だから、レオナルドというのが本名ね。ここで『ピサの』とわざわざ付けるのは、有名な『レオナルドダビンチ』と紛らわしいから？」
「それは違うようじゃ。ちなみに、『レオナルド・ダ・ビンチ』（1452～1519）は、『（Leonardo da Vinci） イタリアの美術家、科学者。フィレンツェ、ミラノ、フランスで活動。絵画では、厳しい観察に基づいた人体・空間表現と深い精神性によって、ルネサンス絵画の頂点を築き、「モナリザ」「最後の晩餐」などの作品を残した。また芸術、人生、人体研究、自然観察、機械設計などに関する多数の素描や覚書がある。広辞苑第7版）』じゃ。これを見ると、フィボナッチは、ダビンチより、約300年前の人じゃ。ピサのレオナルドは、正式には、レオナルド・ダ・ピサという名前じゃそうだ」
「なるほど、『da』というのは、起点や場所の前につけるイタリア語の前置詞なのね。だから、ダビンチさんも、ビンチ生まれという意味だったのか。じゃ、街で会っても『ダビンチさん！』と声をかけては、伝わらないわね」
「簡単には、会えないけどな。とは言え、『フィボナッチ』が何なのかには、答えられていないのう。ウィキペディアの『フィボナッチ数』の項を参照すると、『レオナルド・フィボナッチ』となっていて、フィボナッチが人名と書かれているしな。ま、以下では、フィボナッチ（さん）で統一していこう」
目次へ戻る
「フィボナッチ数列は、第62回『再帰関数（1）（等差・等比数列、フィボナッチ数列、繰り返し処理）』で取り上げている。以下では、そこと少し初期値を変えて、f(0)=1、f(1)=1、f(n+2)=f(n+1)+f(n)で定義される数列を（オリジナルな）『フィボナッチ数列』と呼ぶことにしよう」
「第62回では、2階の差分方程式、f(n+2)=f(n+1)+f(n)、を解くことにより、得られる、ビネ（P.M.Binet：1786－1856）の公式を説明しているわね。
具体的には、f(n)＝ρ^nと置いて、ρに関する特性方程式を書き下ろして根を求める。方程式は、
ρ^2＝ρ+1、
その根は、ρ1＝（1/2+√5/2）、ρ2＝（1/2－√5/2）であり、一般解f(n)＝定数1×ρ1^n+定数2×ρ2^n、と書くことができる。
初期値、f(0)=1、f(1)=1を満足する定数1，定数2を求めて整形すると、『はじめに』にも記載している下記になるということ。
f(n)＝√5·(√5/2 + 1/2)^(n + 1)/5 + √5·(√5/2 － 1/2)^(n + 1)·(－1)^n/5、
綺麗に書くと、
ということね」
「そういうことじゃな。具体的な値は、f(n)をn=0～20で計算すると、
[1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597,
2584, 4181, 6765, 10946]
となり、確かにフィボナッチ数列となっていることが分かる。
ウィキペディアによると、自然界などにフィボナッチ数列の数字が現れるものがあるという。簡単な定義にもかかわらず、様々な分野にフィボナッチ数列あるいは、その類似の数列が出没することから、多くの人が関心を寄せている。世界中に『フィボナッチ数列愛好家』がいらっしゃるらしい。我が国でも、『日本フィボナッチ協会』により、研究発表会が行われているそうだ」
「なるほど。日本評論社の『数学セミナー』の2018年8月号でも『フィボナッチ数の大人の楽しみ方』と題して特集記事が組まれているわ。その中に、『日本フィボナッチ協会』というのがあった」
「ともちゃんが紹介してくれた数セミの内容は、未見じゃが、タイトルの一つに、『対称関数から見たフィボナッチ数』として『斉次完全対称式、べき和対称式、基本対称式の3つの対称関数を使って、フィボナッチ数の拡張を試みています。その議論の中では、ガロア群の可換性やフィボナッチ数列の正値単調非減少整数性などが登場します。フィボナッチ数が「対称関数論、円分体論、組合せ論の3つの領域が交わったところに棲んでいる」という解釈が出てきます。』という文章があった。この『べき和対称式』というのは、第93回で取り上げたニュートンの『同次対称式』のことかと思われるが、興味をそそられる内容だのう」
目次へ戻る
「フィボナッチ数列は、マルコフ過程で表せるのか、という問題を取り上げよう。これは、次のような2次元の行列と状態ベクトルを考えれば可能だ。ベクトルv(n)を下のように定義する。
v(n)＝［Fb(n)，Fb(n+1)］、（n=0～の整数）、初期ベクトルは、v(0)＝［1，1］とおく。
なお、上では、HPで見やすくするため横ベクトルとして書いているが、行列×ベクトルと書きたいので、計算時には、ベクトルに転置をつけることにする。
対応するマルコフ行列Aは、
だな」
「なるほど。この行列Aと状態ベクトルvを使えば、
v(1)＝A×v(0)＝［1，2］、
v(2)＝A×v(1)＝［2，3］、
v(3)＝A×v(2)＝［3，5］、・・・
と順次、フィボナッチ数列が求められるのね」
「ともちゃんの『初なるほど』いただきましたぞ。このことは、私的数学塾：http://shochandas.xsrv.jp/の『私の備忘録』→『数学・・・解析学分野』の『フィボナッチ数を極める』にも記載されていた。ここには、フィボナッチ数列に関する様々な性質が述べられている。
ところで、わしは、第88回『マルコフ過程（1）（非対称型道中双六：宿場数=3～9）』で、初めて『マルコフ過程』を勉強したんじゃが、いきなり、道中双六に応用しようとしたので、計算が面倒になった。
なぜかというと、道中双六のマルコフ行列Aには、要素にパラメーター（推移確率）pが含まれていたからじゃ。フィボナッチ数列を最初の例に取り上げれば、分かりやすかったと思う。例題は、大切だな」
「そうね。では、あたしがマルコフ行列を使って、フィボナッチ数列の一般項を求めるまでをご説明しますね。
DERIVEでは、Aの固有方程式は、CHARPOLY（A，z）で求められ、z^2－z－1＝0、であり、2根をz1、z2とすれば、
z1＝1/2+√5/2、z2＝1/2－√5/2、である。
ついで、マルコフ行列Aの対角化のために2つの固有値に対応する独立な固有ベクトルを求める。
EXACT_EIGENVECTOR(A,z1)＝([1/2 － √5/2; －1])
もうひとつは、
EXACT_EIGENVECTOR(A,z2)＝([√5/2 + 1/2; －1])
である。このEXACT_EIGENVECTOR関数は、厳密な固有値を与えないとゼロベクトルを返すので気をつけて下さい。
これらから、R^－1×A×R＝［［z1，0］，［0，z2］］となる行列Rを構成する。それには、DERIVEのファイルメニュ－の読み込みからユ－ティリティ－で、VectorMatrixFunctions.mthを読み込み、固有ベクトルを横ベクトルにして結合し、再度、転置すればよい。
R＝APPEND([1/2 － √5/2; －1]`, [√5/2 + 1/2; －1]`) `
実行すると対角化行列Rとして、
が得られる。
実際、R^－1×A×Rを作って計算すると
となり、確認できるわ。
次に上の対角化された行列をBと置けば、
である。
前述の関係から、Fb(n)＝A^n×v(0)＝A^n×［1，1］である。この右辺のA^nは、RとBが分かっていると簡単に求められるということだったわね」
「A^nを求めるあたりは、しつこいようだが、丁寧に書けば、
B^n＝（R^－1×A×R）^n＝（R^－1×A×R）×（R^－1×A×R）×・・
＝R^－1×A×I×A×I×・・・×R
＝R^－1×A^n×R、と変形できることを利用するのじゃ。Iは、単位行列じゃ。
従って、R×B^n×R^－1＝A^nが得られる。この際、行列の乗算では、結合法則（A×（B×C）＝（A×B）×C）が常に成り立つことに注意する点かな」
「たしかにね。
そこで、B^nは、
と求められる。
あとは、R×B^n×R^－1×Fb(0)’ を計算するだけなので、結果だけを示すと、
R×B^n×R^－1×v(0)’ ＝［Fb(n)，Fb(n+1)］、（n=0～の整数）から、第1項を取り出して、
Fb(n)＝√5·(√5/2 + 1/2)^(n + 1)/5 + √5·(√5/2 － 1/2)^(n + 1)·(－1)^n/5、
n=0～10まで、ベクトルの第1項Fb(n)のみ計算して表示すれば、
Fb(n) ＝[1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89]
と一般項を計算するビネの公式と同じになったわ」
「一般項を求めるだけに行列の対角化を使うのは、やや、『鶏を割くに牛刀を用いる』の類いで、面倒だな。第89回『マルコフ過程（2）（非対称型道中双六：差分法1）』で紹介しているように差分方程式として解いた方が簡単だ。
第62回の記事では、『再帰関数』の例として、フィボナッチ数列f(n)を取り上げた。再帰関数を使ったフィボナッチ数列の計算速度について、『・・いずれにしても、nが20程度までは、1秒以下で計算できるが、nが30程度まで大きくなると、極度に時間がかかる。・・f(20)は、0.17秒なのに、f(30)では、なんと、16.9秒もかかる』として、ベクトルを使って計算速度を上げる話につなげていったのじゃった。
DERIVEでは、Iterate関数（繰り返しを行う関数）と2次元のベクトルvを使い、数列をF(n)で表すと、この節の初期値に合わせて、
F(n)＝Iterate([v↓2，v↓1+v↓2],v,[1,1],n)
となる。
ちなみに、Iterate関数は、最初に第3引数[1,1]を第2引数vに代入、これが、ベクトルの初期値を決めることになる。
次に第1引数[v↓2，v↓1+v↓2]を計算し、第2引数vに代入する、これを第4引数のn回繰り返す、という関数だ。（初期値の代入を勘定すると第4引数+1回計算する）、そして、得られる（画面に表示される）のは、ベクトルvだ。
n＝30では、[1346269, 2178309]
が表示される。要する時間は、瞬時だった」
「念のため、再帰関数を使った場合を補足しておくわよ。再帰関数をg(n)と書けば、
g(n):= IF(n = 0, 1, IF(n = 1, 1, g(n － 1) + g(n － 2)))
なお、g(n)は、ここでの初期値に合わせるために、IFの入れ子を使っているけど、g(30)を求めるには、15秒程度がかかる」
「そうだな、Iterate関数とベクトルを使うと速度が向上する。しかし、当時は、第1引数内で（v↓1+v↓2）を計算するため、マルコフ過程という意識は、なかった。今回、あらためて、振り返るとそのことがよく分かる。
なお、付け加えると、A^30×［1，1］の計算は、DERIVEでは、対角化するまでもなく、瞬時に行える」
目次へ戻る
「フィボナッチ数列の母関数については、第62回でも取り上げたわね。母関数は、1/（1－x－x^2）という有理関数だった。
1/（1－x－x^2）＝・・+89·x^10 + 55·x^9 + 34·x^8 + 21·x^7 + 13·x^6 + 8·x^5 + 5·x^4
+ 3·x^3 + 2·x^2 + x + 1、
逆順に表示していて見苦しいでしょうが、ご勘弁のほどを。変数x^nの係数がフィボナッチ数列となるのよ。
えーと、そもそも、母関数とは、何かというと、数列、f(n)が、
母関数＝Σ（n=0～∞）f(n)×x^n、となるものなのね。こういうのは、『通常型母関数』と言われるタイプ。
一方、1/n!の因子が陽に表れる『指数型母関数』もある。ベルヌーイ数列で出たきたわね。具体的には、第63回『再帰関数（2）（数列の母関数、固有値のべき乗法）』を参照して下さいな。
フィボナッチ数列は、通常型母関数で、
となり、このf(n)が初期値f(0)=1、f(1)=1の場合のフィボナッチ数列となるのね」
「ここで、多くの方が母関数の分母が特性方程式/固有方程式に似ていることに気がつかれるじゃろう。後述するが、母関数（全体）は、当然ながら、初期値にもよるため、固有方程式のみでは、構成できないものの、特性方程式/固有方程式と深く関係している。
その前に、母関数の応用例の一つとして、組み合わせ記号により、フィボナッチ数列を表してみよう。これは、1+r+r^2+・・＝1/(1－r)、という等比数列の公式から、1－x－x^2＝1－x（1+x）と書き換えて、母関数を公比r＝x（1+x）の無限級数と考えれば、
1/（1－x－x^2）
＝Σ（k=0～∞）（x^k×(1+x)^k）
＝Σ（k=0～∞）（x^k×Σ（j=0～k）（Comb(k，j)×x^j）
＝Σ（k=0～∞）x^k（kC0 x^0+kC1 x^1+kC2 x^2+・・+kCkx^k）
＝Σ（k=0～∞）（kC0 x^k+kC1 x^(k+1)+kC2 x^(k+2)+・・+kCk x^2k）
ここで、Comb(k，j)をkCjと書いた。
今、x^nの係数を集めてみると、それは、
nC0 +n-1C1 +n-2C2 +・・+0Cnであることが見て取れる。
従って、初期値f(0)=1、f(1)=1の場合のフィボナッチ数列f(n)は、
f(n)＝Σ（j=0～n）Comb(n－j，j)
とも書き表すことができるじゃろう」
「実際、n=0～10まで計算すると、[1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89]となって、フィボナッチ数列を再現しているわね」
目次へ戻る
「この節では、f(0)、f(1)が必ずしも、1、1、ではない、フィボナッチ数列を考えてみよう。ただし、f(n+2)＝f(n+1)+f(n)、という関係は、変わらないとする。
ここで、素朴に母関数を構成する方法を考えよう。フィボナッチ数列の母関数をφ(x)とすれば、母関数の定義から、
φ(x)＝Σ（n=0～）f(n)×x^n、であるが、
今、φ(x)＝a/(1－αx) + b/(1－βx)、と仮定してみよう。このα、βは、特性方程式の根ではなく、ただのパラメ－タ－と考える。
等比級数の公式を思い出せば、
φ(x)＝Σ（n=0～）｛a×(αx)^n + b×(βx)^n｝
＝Σ（n=0～）｛（a α^n + b β^n）x^n｝
と書くことができよう。
すると、f(n)＝（a α^n + b β^n）と書ける。
フィボナッチ数列の初期値を一般的にするため、c、dを実数として、初期値f(0)＝c、f(1)＝d、の条件を満たすことを要求すると、
f(n)＝（a α^n + b β^n）から、
a + b = c、a·α + b·β = d、が必要。よって、
[a = (c·β － d)/(β － α) ∧ b = (c·α － d)/(α － β)]、が成り立つ。
次にf(n+2)＝f(n+1)+f(n)からの条件からは、n=2、3と置いて、それぞれ、
a·α^2 + b·β^2 = c + d、a·α^3 + b·β^3 = c + 2·d、
ここで、aとbを先ほどの式で置き換えれば、
d·(α + β) － c·α·β = c + d、
d·(α^2 + α·β + β^2) － c·α·β·(α + β) = c + 2·d
となり、これから、α、βについて、
α = (√5 + 1)/2 ∧ β = 1/2 － √5/2,
または
α = (1 － √5)/2 ∧ β = √5/2 + 1/2
が得られる。
αとβは、交換可能なので、前者の組を採用すれば、
α = (√5 + 1)/2 ∧ β = 1/2 － √5/2,
これが、特性方程式の2根、ρ1とρ2とも等しいことは、すぐ分かる。
よって、a、bは、
([a = c·(1/2 － √5/10) + √5·d/5 ∧ b = c·(√5/10 + 1/2) － √5·d/5])
結局、母関数φ(x)は、
φ(x)＝Σ（n=0～）｛（a α^n + b β^n）x^n｝の（ ）内は、
(√5·2^(－n － 1)·(√5 + 1)^n·(c·(√5 － 1) + 2·d)/5 + √5·2^(－n － 1)·(√5 － 1)^n·(c·(√5 + 1) － 2·d)·(－1)^n/5)
綺麗な形に書き直すと、
(√5/2 + 1/2)^n·(－ c·(1/2 － √5/2) + d)/√5)+ ((1/2 － √5/2)^n·(c·(√5/2 + 1/2) － d)/√5)
同じことだが、
となる」
「なるほど。これが初期値が［c，d］というフィボナッチ数列の一般項ね。
ちなみに、n=0～10まで計算してみると、
f(n)＝([c, d, c + d, c + 2·d, 2·c + 3·d, 3·c + 5·d, 5·c + 8·d, 8·c + 13·d, 13·c + 21·d, 21·c + 34·d, 34·c + 55·d])となるので、
たしか。明らかに、c=d=1とした場合は、先に取り上げた（オリジナルの）『フィボナッチ数列』と同じなるわね」
「一方、φ(x)＝a/(1－αx) + b/(1－βx)から、母関数は、閉じた式として、
φ(x)＝(c － x·(c － d))/(1 － x － x^2)
が得られる。
なお、オリジナルのフィボナッチ数列では、c=d=1として、φ(x)＝1/（1－x－x^2）に帰着することが分かるじゃろう。紛らわしいが、分母は、特性方程式（固有方程式）（1+x－x^2）そのものではないことに注意して欲しい」
目次へ戻る
「（5）では、初期値が一般のフィボナッチ数列を考えた。この節では、初期値だけでなく、差分方程式の係数も異なる数列、g(n)、を考えてみよう。初期値は、前節と同様に、g(0)＝c、g(1)＝d、とする。
一方、差分方程式を、次のように表す。
g(n+2)＝p×g(n+1)+q×g(n)、
ただし、pとqは、実数のパラメ－タ－である。（p、qは、道中双六の推移確率とは、無関係）、
この数列の一般項を求めてご覧。とは言っても、前節の方法では、大変だから、固有値を求めて、そのn乗の式の一次結合から計算するのが吉じゃろう」
「わかりやした。g(n)＝ρ^n、置いて、得られる特性方程式の根をα、βとすれば、
α＝(p+√(p^2 + 4·q))/2、
β＝(p－√(p^2 + 4·q))/2、
と2つの固有値が求まる。
すると、差分方程式の一般解は、g(n)＝a×α^n+b×β^nの形となるので、
（今は、2重根でないと仮定する、すなわち、α<>β、である。）
初期値g(0)＝c、g(1)＝dから、
g(n)＝(2^(－n － 1)·(p － w)^n·(c·(p + w) － 2·d)/w + 2^(－n － 1)·(p + w)^n·(2·d － c·(p － w))/w)
ただし、w＝√(p^2+4q)、が得られる。
綺麗な形に整理すると、（こいつはDERIVEでは、難しいわね）
となる。
ちなみに、n=0～10までを計算すると、wを√(p^2+4q)で置き換えて、
([c, d, c·q + d·p, c·p·q + d·(p^2 + q), c·q·(p^2 + q) + d·p·(p^2 + 2·q),
c·p·q·(p^2 + 2·q) + d·(p^4 + 3·p^2·q + q^2), c·q·(p^4 + 3·p^2·q + q^2)
+ d·p·(p^4 + 4·p^2·q + 3·q^2), c·p·q·(p^4 + 4·p^2·q + 3·q^2) + d·(p^6 +
5·p^4·q + 6·p^2·q^2 + q^3), c·q·(p^6 + 5·p^4·q + 6·p^2·q^2 + q^3) + d·p·(p^6
+ 6·p^4·q + 10·p^2·q^2 + 4·q^3), c·p·q·(p^6 + 6·p^4·q + 10·p^2·q^2 + 4·q^3)
+ d·(p^8 + 7·p^6·q + 15·p^4·q^2 + 10·p^2·q^3 + q^4), c·q·(p^8 + 7·p^6·q
+ 15·p^4·q^2 + 10·p^2·q^3 + q^4) + d·p·(p^8 + 8·p^6·q + 21·p^4·q^2 + 20·p^2·q^3
+ 5·q^4)])
と正しくg(n)を再現することが分かった」
「一応、マルコフ行列とベクトルを使っても、検証しておこう。
また、ベクトルとして、v=［g(n)，g(n+1)］と置けば、初期値は、［c，d］なので、
g(n)だけ取り出すと、
と書くことができる。
なお、ベクトルの右肩の ’は、ベクトルの転置、右辺全体の下付き添え字1は、ベクトルの1番目の要素を取り出す意味。
ここで、n=0から10までを計算すると、
([c, d, c·q + d·p, c·p·q + d·(p^2 + q), c·(p^2·q + q^2) + d·p·(p^2 + 2·q),
c·p·q·(p^2 + 2·q) + d·(p^4 + 3·p^2·q + q^2), c·q·(p^4 + 3·p^2·q + q^2)
+ d·p·(p^2 + q)·(p^2 + 3·q), c·p·q·(p^2 + q)·(p^2 + 3·q) + d·(p^6 + 5·p^4·q
+ 6·p^2·q^2 + q^3), c·q·(p^6 + 5·p^4·q + 6·p^2·q^2 + q^3) + d·p·(p^2 +
2·q)·(p^4 + 4·p^2·q + 2·q^2), c·p·q·(p^2 + 2·q)·(p^4 + 4·p^2·q + 2·q^2)
+ d·(p^8 + 7·p^6·q + 15·p^4·q^2 + 10·p^2·q^3 + q^4), c·q·(p^8 + 7·p^6·q
+ 15·p^4·q^2 + 10·p^2·q^3 + q^4) + d·p·(p^8 + 8·p^6·q + 21·p^4·q^2 + 20·p^2·q^3
+ 5·q^4)])
となり、
ともちゃんが計算してくれたベクトルから引き算すると、
([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0])とゼロベクトルとなり、両者が一致していることを確かめられた。
さて、このg(n)の母関数をψ(x)とすれば、
ψ(x)＝Σ（n=0～）g(n)×x^n、である。
ここで、
ψ(x)＝｛(d－c(p/2－w/2))/w｝(1/(1－γx))+｛(c(p/2+w/2)－d)/w｝1/(1－δx)、
と置いてみよう。
なお、γ＝(p/2+w/2)、δ＝(p/2－w/2)である。
ψ(x)＝Σ［｛(d－c(p/2－w/2))/w｝γ^n+｛(c(p/2+w/2)－d)/w｝δ^n］x^n、
となり、ψ(x)＝Σ（n=0～）g(n)×x^n、の形になるだろう。
一方、ψ(x)は、
ψ(x)＝(x·(c·p － d) － c)/(q·x^2 + p·x － 1)
となる。
綺麗な形に整理すれば、
だな」
「じゃ、試しに、x=0でψ(x)をテイラ－展開してみると、下の表のようになって、確かに母関数であることが確認できる」
|
n |
母関数のx=0でのテイラ－展開 |
差分方程式g(n) |
|
5 |
c·p·q·(p^2 + 2·q) + d·(p^4 + 3·p^2·q + q^2) |
c·p·q·(p^2 + 2·q) + d·(p^4 + 3·p^2·q + q^2) |
|
4 |
c·q·(p^2 + q) + d·p·(p^2 + 2·q) |
c·q·(p^2 + q) + d·p·(p^2 + 2·q) |
|
3 |
c·p·q + d·(p^2 + q) |
c·p·q + d·(p^2 + q) |
|
2 |
c·q + d·p |
c·q + d·p |
|
1 |
d |
d |
|
0 |
c |
c |
「なお、wが実数であるためには、平方根内のp^2+4q>=0が必要だ。
特にw＝0は、特性方程式が2重根を取る場合だ。
具体的には、q＝－p^2/4、に相当する。
α＝(p+√(p^2 + 4·q))/2、β＝(p－√(p^2 + 4·q))/2、なので、
2重根の場合は、α＝β＝p/2、となるため、
このときは、β^nの代わりに、n×α^n、がもう一つの一次独立な特別解となり一般解は、これらの一次結合となる。
一方、先のg(n)の式でw→0の極限を計算すると、
g(n)＝2^(－n)·p^(n － 1)·(2·d·n － c·p·(n － 1))
と正しく計算されていることが分かる。すなわち、2重根の場合の母関数もψ(x)でよい。
ψ(x)において、c=d=1、かつ、p=q=1と置けば、オリジナルのフィボナッチ数列の母関数、
φ（x）＝1/(1－x－x^2)に帰着する。
付け加えると、フィボナッチ数列と類似の『リュカ数列』（g(0)=2、g(1)＝1、p=q=1）では、母関数は、
ψ(x)＝(2－x)/(1－x－x^2)、
となる。
観察すると、母関数の分母は、特性方程式（ρ^2－pρ－q=0）において、単にρ→xと置き換えるのではなく、特性方程式をρ^2で割った式（1－p/ρ－q/ρ^2）において、1/ρ→xと置き換えたものに等しい。分子部分は、xの1次式と仮定して、初期条件からその2つの未知係数を定めれば、リュカ数列の母関数の分子の2－xが求められる」
目次へ戻る
「こうなると、3階以上の差分方程式で定義されるフィボナッチ数列が気になるわね」
「確かにのう。実は、ウィキペディアの『フィボナッチ数』の項目には、3階以上についても言及されている。
それによると、3階のものは、『トリボナッチ数列』と呼ばれて、
T(n+3)＝T(n+2)+T(n+1)+T(n)、
で定義されるフィボナッチ数列に類似した数列だ。
ウィキペディアに記載されている一般項は、
ただし、α～γは、特性方程式、x^3－x^2－x－1＝0の3根で、αは、唯一の実根、残りの二つは、複素根である。
しかし、一般項からT(n)を計算するのは、面倒だ。
だが、面白いのは、上の一般項の式は、α、β、γに関して『対称式』であることだ。対称式が基本対称式に分解できることは、第93回で学んだ。基本対称式は、特性方程式の『根と係数の関係』で結びついているので、方程式の係数のみで、T(n)は、計算可能である。以下では、ギリシア文字を書くのが面倒なので、α＝x1等と記載する。
このとき、変数が3個の際の基本対称式を、s1、s2、s3として、
s1＝x1+x2+x3
s2＝x1 x2+x2 x3+x3 x1
s3＝x1 x2 x3、
とする。
例えば、T(3)=x1+x2+x3、となるので、これは、基本対称式のs1で、
方程式を、x^3+a2x^2+a1x+a0＝0、と書き表したときの根と係数の関係から、
2次項の係数＝a2＝－(z1 + z2 + z3)＝－s1
1次項の係数＝a1＝(z1z2 + z1z3 + z2·z3)＝s2
0次項の係数＝a0＝－z1·z2·z3＝－s3、であり、
今回、x^3－x^2－x－1＝0、なので、a2＝－1、a1＝－1、a0＝－1、
よって、s1＝1、s2＝－1、s3＝1、となる。
従って、T(3)＝s1＝1、と根の計算を経ずに求められる。
また、T(4)＝x1^2 + x1·x2 + x1·x3 + x2^2 + x2·x3 + x3^2、
この対称式を基本対称式に分解する『ウェアリングの方法』を使うために、第93回『マルコフ過程（6）（非対称型道中双六：平均日数と対称式）』で利用したDERIVEのユーザー定義関数、Freset（3）を実行後にユーザー定義関数、Fg（T(4)、x1^2，3）を実行すると、
T(4)＝s1^2－s2、と分解できる。
従って、
T(4)＝s1^2－s2＝１－(－1)＝2、となるじゃろう」
「なるほど。T(5)は、というと、
T(5)＝x1^3 + x1^2·(x2 + x3) + x1·(x2^2 + x2·x3 + x3^2) + x2^3 + x2^2·x3 + x2·x3^2 + x3^3
＝s1^3 － 2·s1·s2 + s3
＝(1)^3－2(1)(－1)+(1)＝4、となって、正しいわ」
「ま、以上は、原理的なことで、実用上は、これでは、たまらんので、元の差分方程式、又は、マルコフ行列と状態ベクトルから計算した方が便利なことは、言うまでもない。
とは言え、4階以上でも、一般項を3階のような根を使った形で書いても、根を計算せずに一般項の値を求めることが原理的には、可能なことが分かると思う。
さて、トリボナッチ数列のマルコフ行列は、
であり、状態ベクトル、vを、
V＝［T(n)，T(n+1)，T(n+2)］
とすれば、
A×V ' ＝［T(n+1)，T(n+2)，T(n+3)］’ である。
初期値 ［0，0，1］ では、
T(n)＝[0, 0, 1, 1, 2, 4, 7, 13, 24, 44, 81,・・]
初期値 ［1，1，1］ では、
T(n)＝[1, 1, 1, 3, 5, 9, 17, 31, 57, 105, 193,・・]
と求められる。
なお、ウィキペディアに記載されているように、T(n+1)/T(n)を計算すると、n=0～20で、
([1, 1, 3, 1.666666666, 1.8, 1.888888888, 1.823529411, 1.838709677, 1.842105263,
1.838095238, 1.839378238, 1.839436619, 1.839203675, 1.839300582, 1.839293798,
1.839281319, 1.839288103, 1.839287013, 1.83928642, 1.839286866, 1.839286758])
となって、一定の値に収束するように見える。これは、z^3－z^2－z－1＝0のただ一つの実根、前述のα、
α= (19 － 3·√33)^(1/3)/3 + (3·√33 + 19)^(1/3)/3 + 1/3)
≒1.839286755・・である。これを『トリボナッチ定数』というそうだ」
「なるほど。オリジナルのフィボナッチ数列では、f(n+1)/f(n)は、黄金比＝（1+√5）/2≒1.618033988、に収束するんだったわね。
実際、初期値［1，1]のフィボナッチ数列の一般項をf(n)と書いて、f(n+1)/f(n)を0～20まで計算してみると、
([1, 2, 3/2, 5/3, 8/5, 13/8, 21/13, 34/21, 55/34, 89/55, 144/89, 233/144, 377/233, 610/377, 987/610, 1597/987, 2584/1597, 4181/2584, 6765/4181, 10946/6765, 17711/10946])
すなわち、
([1, 2, 1.5, 1.666666666, 1.6, 1.625, 1.615384615, 1.619047619, 1.617647058, 1.618181818, 1.617977528, 1.618055555, 1.618025751,
1.618037135, 1.618032786, 1.618034447, 1.618033813, 1.618034055, 1.618033963,
1.618033998, 1.618033985])
となり、n=20程度で、ほぼ、9桁まで収束している。
しかし、ビックリ。4階の『テトラナッチ数列』、5階の『ペンタナッチ数列』もあるなんてね」
「ウィキペディアには、さらに、6～12階までの名称（6階は、ヘキサナッチ数列など）と2通りの初期値（状態ベクトルの最後の要素のみ1で以外はゼロと初期値がすべて1のもの）に対応する数列へのリンクが付されていた。とは言え、4階以上の数列もマルコフ行列とベクトルを使えば、計算は、簡単だろう」
「母関数を使って定義する方法もあるわ。
3階のトリボナッチ数列、T(n)を表す母関数は、
［0，0，1］からは、φ(x)＝－ x^2/(x^3 + x^2 + x － 1)
10次までのテイラー展開から、
(81·x^10 + 44·x^9 + 24·x^8 + 13·x^7 + 7·x^6 + 4·x^5 + 2·x^4 + x^3 + x^2)
※0次と1次は、初期値として、T(0)＝T(1)=0、としているため、（係数がゼロとなり）xの0次と1次の項は、現れない。
一方、初期値が［1，1，1］からは、
φ(x)＝((x^2 － 1)/(x^3 + x^2 + x － 1))
10次までのテイラー展開から、
(193·x^10 + 105·x^9 + 57·x^8 + 31·x^7 + 17·x^6 + 9·x^5 + 5·x^4 + 3·x^3
+ x^2 + x + 1)
母関数によれば、根を求めずとも一般項を表現できるということを示せたかしら」
目次へ戻る
「非対称道中双六の『道中双六』とは、昔からある絵双六のことだな。わざわざ、『非対称』と銘打っているのは、マルコフ過程でよく取り上げられる対称型（振り出しの後ろへも戻れ、上がりに対応して下がり？もある対称的な双六）と区別するためだ。
下の図は、宿場が3つ（c＝宿場数+1として、c=4）のもの。
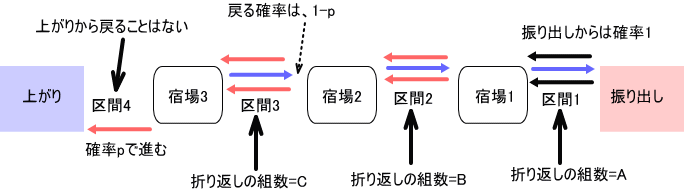
双六は、次のルールで進める。
1.駒は、振り出しから、確率1で、宿場1に進むことができる。
2.駒は、各宿場で、確率 pで、次の宿場に進み、確率 (1－p)で1つ戻るものとする。
3.駒が最後の宿場から上がりに進んだときは、双六上から消える。（上がりから戻ることはない）
4.駒どおしの関係は、無いものとする。
5.振り出しから宿場まで、各宿場間、最後の宿場と上がりまでの所要時間は、同一とし、1（日）と勘定する。
というもので、振り出しから上がりまでの平均日数は、最短日数（＝c）の何倍か？、というものだった」
「もともとは、2014年（午年）の年賀状で、おじぃさんが取り上げた題材が宿題になっているの。（自業自得だわね！）
最初は、c=2と3のケースしか、平均日数の厳密解が出せなかった。もっとも、p=1/2については、cが大きいものとして、偏微分方程式で近似して、平均日数＝c^2、となることが証明できたと思うんだけど、cが小さな離散的なケースでは、c=4で壁にぶつかっていた。
それが、マルコフ過程を（ちょっと）勉強したおかげで、c=4が解けたことをきっかけに、平均日数の公式を求められたの。ただ、ある対称式を基本対称式に分解する手間が必要となり、前に書いたようにc=10までしか、厳密には、計算していないけどね」
「ともちゃん、非対称道中双六の問題の紹介、ありがとさん。いや、ずいぶん、楽しませてもらっているテーマになったものだ。我ながら、飽きないことに感心する。今日のようなコロナ自粛では、まったく、有り難いものじゃ。
さて、ともちゃんに紹介してもらった、第87回の『道中双六の問題（補筆3）（今後の課題）』では、m＞＝0の整数、c＝宿場数+1とした際、『非対称道中双六』において、2m+c日目に上がる確率をf(2m+c)と書くとき、
f(2m+c)＝（1－p）^m p^(c－1) Σ（k1+k2+・・＋kc－1=m）（p^（m－k1）Comb（k1+k2，k1） Comb（k2+k3，k2）・・Comb（kc－2+kc－1，kc－2））と書けることを説明している。
ここで、k1～kc－1は、ゼロまたは正の整数で、Σは、k1+k2+・・＋kc－1=mを満たすk1～kc－1のすべての組み合わせについて合計する。これにより、平均日数は、
平均日数＝Σ（m=0～∞）（2m+c）×f(2m+c)と書くことができた。
しかし、c>3では、f(2m+c)＝（1－p）^m p^(c－1) Σ（k1+k2+・・＋kc－1=m）（p^（m－k1）Comb（k1+k2，k1） Comb（k2+k3，k2）・・Comb（kc－2+kc－1，kc－2））、を厳密に計算することができずに苦しんだ。ともちゃんが言うようにマルコフ過程のアイデアを取り入れて、だいぶ、解明できた気は、するのう。（青字個所を追記。2020/5/13）
ここで、ひと言、お断りしておくと、マルコフ過程の考えから導いた平均日数の公式では、上で述べた、f(2m+c)、すなわち、
f(2m+c)＝（1－p）^m p^(c－1) Σ（k1+k2+・・＋kc－1=m）（p^（m－k1）Comb（k1+k2，k1） Comb（k2+k3，k2）・・Comb（kc－2+kc－1，kc－2））、を利用していない。つまり、平均日数の異なった表現を与えていると考えられる。いずれ、両者が同じものであるという直接的な証明が可能だとは、思っている。
第93回で、c=4、6，8，10、について、平均日数の厳密解を計算でき、cが奇数の3、5については、第89回『マルコフ過程（2）（非対称型道中双六：差分法1）』で済んだ。また、c=7は、第90回「マルコフ過程（3）（非対称型道中双六：平均日数計算公式）」で検証した。従って、第88回『マルコフ過程（1）（非対称型道中双六：宿場数=3～9）』で記載した平均日数の推定式の厳密な検証が済んでいないのは、cが10以下では、c＝9のみになっていたが、その後、第95回「マルコフ過程（7）（非対称道中双六：宿場数=8の平均日数）」で検証している」
目次へ戻る
「そこで、今回、方向を変えて、c＝4の場合の上がる確率、f(2m+4)の本質的部分である、
fsum(m，p)＝Σ（k1+k2+k3=m）（p^（m－k1）Comb（k1+k2，k1） Comb（k2+k3，k2））、
という級数を調べてみることにした訳じゃ。※f(2m+4)＝fsum(m，p)×(1－p)^m×p^3、である。
この級数、fsum(m，p)は、実は、以下のfs(m,p)と等しい。
ただし、
である。
これは、c=4の平均日数の計算過程の副産物として得られた。ちょっと見では、本当かいと疑われるかも知れないので、まずは、最初の方を計算して正しいかどうかを確かめて欲しい」
「じゃ、k1、k2、k3と書くのは、面倒なので、a、b、cで表すことにしましょう。
fsum(m,p)＝Σ（a+b+c=m）（p^（m－a）Comb（a+b，a） Comb（b+c，b））、
Comb(n,r)は、DERIVEの組み合わせ数を表す関数、普通、数学では、nCr、などと書かれるもの。
さて、fsumと等しいのが、fs(m,p)で、
fs(m,p)＝2^(－m － 1)·((√(4·p^2 + 1) + 2·p + 1)^(m + 1) － (－ √(4·p^2 + 1)
+ 2·p + 1)^(m + 1))/√(4·p^2 + 1)
＝2^(－m － 1)·((√(4·p^2 + 1) + 2·p + 1)^(m + 1) － (－ √(4·p^2 + 1) + 2·p + 1)^(m + 1))/√(4·p^2 + 1)
ここで、wは、√(4p^2+1)、
Deriveでm＝0～20まで、計算してみた。fsumの最初の方のみを書き出すと、
[1, 2·p + 1, 4·p^2 + 3·p + 1, 8·p^3 + 8·p^2 + 4·p + 1, 16·p^4 + 20·p^3 + 13·p^2 + 5·p + 1, 32·p^5 + 48·p^4 + 38·p^3 + 19·p^2 + 6·p + 1・・・]
fsの計算結果（ここでは記載してないけど）も同様に見えるが、念のため、ベクトル同士を引き算すると、
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
となり、両者が（少なくともm=0～20までは）等しいことがあらためて確かめられたわ」
「正しいのは、当然なんだが、あらためて、計算してもらって安心した。
このfs(m,p)を見ているとフィボナッチ数列の一般項（ビネの公式）と似ている気がするじゃろう。フィボナッチ数列については、2.『フィボナッチ数列』でいろいろと勉強してきた。
2.（6）で取り上げた『一般のフィボナッチ数列』の一般項をg(n)と書けば、
初期値、g(0)＝c、g(1)＝d、g(n+2)＝α×g(n+1)+β×g(n)、の一般項、g(n)は、
g(n)＝(2^(－n － 1)·(α － u)^n·(c·(α + u) － 2·d)/u + 2^(－n － 1)·(α + u)^n·(2·d
－ c·(α － u))/u)
ただし、u＝√(α^2+4β)、が得られる。（2.（6）のp、q、wをこの節に合わせて、α、β、uに変えています）
見やすい形に整理すれば、
ただし、
であった。
ともちゃん、どのような一般フィボナッチ数列、g(n)であれば、fsを再現できるかを調べて欲しいのう」
「一般のフィボナッチ数列の一般項は、g(n)は、
初期値［c，d］、差分方程式g(n+2)＝α×g(n+1)+β×g(n)、を満たし、
g(n)＝(2^(－n － 1)·(α － √(α^2 + 4·β))^n·(c·(√(α^2 + 4·β) + α) － 2·d)/√(α^2
+ 4·β) + 2^(－n － 1)·(√(α^2 + 4·β) + α)^n·(c·(√(α^2 + 4·β) － α) + 2·d)/√(α^2
+ 4·β))
なのね。
一方、fs(n，p)は、（mをnと置き換えてある）
fs(n,p)＝(((√(4·p^2 + 1) + 2·p + 1)/2)^(n + 1)/√(4·p^2 + 1) － (－ (√(4·p^2
+ 1) － 2·p － 1)/2)^(n + 1)/√(4·p^2 + 1))
二つを等値して、n=0と置けば、
c=1が得られる。
次に、n=1と置いて、
d=2p+1を得る。
さらに、n=2、n=3、から、α、βについて、
(2·p·α + α + β = 4·p^2 + 3·p + 1)
(2·p·(α^2 + β) + α^2 + α·β + β = 8·p^3 + 8·p^2 + 4·p + 1)
の2式が得られるので、これらを解いて、
α = 2·p + 1、
β = －p、
となり、これで、4つの未知数がわかった。
念のために、g(n)の一般項に、これらのc、d、α、βを代入してみると、
g(n)=(((√(4·p^2 + 1) + 2·p + 1)/2)^(n + 1)/√(4·p^2 + 1) － (－ (√(4·p^2
+ 1) － 2·p － 1)/2)^(n + 1)/√(4·p^2 + 1))となる。
ここで、w=√(4p^1+1)と置き替えると、
g(n)=(((2·p + w + 1)/2)^(n + 1)/w － ((2·p － w + 1)/2)^(n + 1)/w)
すなわち、
となる。
これは、下図のfs(m，p)のmをnにしたもので、まったく同一であることが分かる。
ということで、分かったわ」
「これは、良かった。
すると、繰り返しになるが、fs(m，p)は、
初期値［1，2p+1］、
差分方程式が、g(n+2)＝（2p+1）g(n+1)－p g(n)、
である一般のフィボナッチ数列の一般項と等しいということになったな。
すると、その母関数をψ(x，p)と書けば、2.（6）の結果から、
ψ(x，p)＝(x·(c·α － d) － c)/(β·x^2 + α·x － 1)
＝1/(p·x^2 － x·(2·p + 1) + 1)、となるはずだ。
実際、x=0でテイラー展開してみると、0～10次までで、
(x^10·(1024·p^10 + 2816·p^9 + 4096·p^8 + 4048·p^7 + 2972·p^6 + 1683·p^5
+ 743·p^4 + 253·p^3 + 64·p^2 + 11·p + 1) + x^9·(2·p + 1)·(256·p^8 + 512·p^7
+ 592·p^6 + 464·p^5 + 269·p^4 + 116·p^3 + 37·p^2 + 8·p + 1) + x^8·(256·p^8
+ 576·p^7 + 688·p^6 + 552·p^5 + 321·p^4 + 138·p^3 + 43·p^2 + 9·p + 1) +
x^7·(2·p + 1)·(64·p^6 + 96·p^5 + 88·p^4 + 52·p^3 + 22·p^2 + 6·p + 1) +
x^6·(64·p^6 + 112·p^5 + 104·p^4 + 63·p^3 + 26·p^2 + 7·p + 1) + x^5·(2·p
+ 1)·(16·p^4 + 16·p^3 + 11·p^2 + 4·p + 1) + x^4·(16·p^4 + 20·p^3 + 13·p^2
+ 5·p + 1) + x^3·(2·p + 1)·(4·p^2 + 2·p + 1) + x^2·(4·p^2 + 3·p + 1) +
x·(2·p + 1) + 1)、となる。
一方、マルコフ行列とベクトルからは、
これのn乗を初期ベクトル［1，2p+1］' に掛けると、
n=0～10までで、
([1, 2·p + 1, 4·p^2 + 3·p + 1, (2·p + 1)·(4·p^2 + 2·p + 1), 16·p^4 + 20·p^3
+ 13·p^2 + 5·p + 1, (2·p + 1)·(16·p^4 + 16·p^3 + 11·p^2 + 4·p + 1), 64·p^6
+ 112·p^5 + 104·p^4 + 63·p^3 + 26·p^2 + 7·p + 1, (2·p + 1)·(64·p^6 + 96·p^5
+ 88·p^4 + 52·p^3 + 22·p^2 + 6·p + 1), 256·p^8 + 576·p^7 + 688·p^6 + 552·p^5
+ 321·p^4 + 138·p^3 + 43·p^2 + 9·p + 1, (2·p + 1)·(256·p^8 + 512·p^7 +
592·p^6 + 464·p^5 + 269·p^4 + 116·p^3 + 37·p^2 + 8·p + 1), 1024·p^10 +
2816·p^9 + 4096·p^8 + 4048·p^7 + 2972·p^6 + 1683·p^5 + 743·p^4 + 253·p^3
+ 64·p^2 + 11·p + 1])
を得る。
先ほどの展開項と比べると同一であることが分かるというところまできた。
fsum(m+2，p)＝（2p+1）×fsum(m+1，p)－p×fsum(m，p)、という意味になる。
しかし、fsumの級数から、fsへの変形に、この結果がどのように役立つかというところで、時間切れじゃ。続きは、次回に持ち越そう。
いや、ともちゃんもお疲れさんじゃったな」
「おじぃさんも、コロナ感染に注意して下さいね」
目次へ戻る
作成日：2020/5/8
誤字を訂正 2020/5/9
表現を微修正 2020/5/10、5/12～5/13
c=7は解決済みと訂正 2020/7/15
c=9を第95回で検証済みと追記 2020/7/22
