「そうだったわね。c=偶数の場合だけ、従来のΨの2倍を新ΨとするようにΨの定義を見直したんだった。それによって、c=偶数の平均日数は、Ψ/p^(2c-3)、ただし、c=2s、s=1、2、・・。と書くことができる。ということだったのね。でも、そもそも、どうして、偶数の場合だけ手直ししたのかしら？」1.平均日数公式の新予想
（1）Ψの定義の一部見直し
（2）新Ψの一覧表（c=2~10）
（3）新Ψの準2次形式予想
2.準2次形式予想による未定係数の求め方
（1）定数項
（2）未定係数を求めるのが面倒な訳
（3）α、γを求める
① sk=1、以外をゼロ
② sk=－1、以外をゼロ
（4）βの項を求める
① 一部に数値解を使う方法
② ∂(sj,xj)=1、以外をゼロ
3.既知の例で検証
（1）c=6（宿場数=5)
① 基礎データ
② DERIVEのユーザー定義関数
③ α、β、γの計算と検算
4.Ψのuk分解(2020/9/13追記)
（1）uk分解の例（c=6）
（2）Ψのuk分解
「非対称型道中双六で、c=宿場数+1、確率pをパラメーターとしたとき、これまで、c=2～10について、平均日数をpの有理式で表す厳密解が得られているのだな。これらを元に第95回『マルコフ過程（7）（非対称型道中双六：宿場数=8の平均日数）』の第3章で、平均日数公式を構成する『新しいΨ』を定義したのを、ともちゃんは、覚えておるかのう」
「そうだったわね。c=偶数の場合だけ、従来のΨの2倍を新ΨとするようにΨの定義を見直したんだった。それによって、c=偶数の平均日数は、Ψ/p^(2c-3)、ただし、c=2s、s=1、2、・・。と書くことができる。ということだったのね。でも、そもそも、どうして、偶数の場合だけ手直ししたのかしら？」
「それは、第90回『マルコフ過程（3）（非対称型道中双六：平均日数計算公式）』で平均日数の計算公式を導いた際にさかのぼるのじゃ。
cが偶数、すなわち、c=2s、s=1、2、・・、の場合、平均日数は、下式で表される。
ここで、xiは、マルコフ行列の固有方程式の解、すなわち、固有値の2乗だ。その後、第93回の『マルコフ過程（6）（非対称型道中双六：平均日数と対称式）』で、Σ内がxiの対称式であることに気がつき、それをΨと書いて、
平均日数=2×p×Ψ/p^(2c-2)=2×Ψ/p^(2c-3)、のように表した。この中のΨは、今までの（旧）Ψだ。
一方、奇数の場合、c=2s+1、s=1～、として、平均日数は、
となる。
奇数の場合は、2の因子がくくり出されないので、
平均日数=p×Ψ/p^(2c-2)=Ψ/p^(2c-3)、と書いたのだ。
ところが、第95回の第3章で、これまで、得られた平均日数の厳密解を基本対称式で表現して、一覧表で、眺めたところ、c=偶数のΨの定義を見直して、2をくくり出さずにΨの中に含めておく方が良いことが分かった。それで、cの偶奇によらずに、平均日数をΨ/p^(2c-3)と書くことにしたのじゃ。これにより、cが偶数の場合のみ、新Ψ=2×従来のΨ、ということになった」
「なるほどね。次の節に第95回の一覧表を再掲したわ」
目次へ戻る
薄い赤色のところがcが偶数の場合。
| c | s | 新しいΨの基本対称式による表現 | 備考 |
| 2 | 1 | －2u1s1+2u1 | s1^2はない |
| 3 | 1 | －u2s1+3u2 | s1^2はない |
| 4 | 2 | 4·s1^2·u3-2·s1·s2·u3-4·s1·(2·u3+u5)+2·s2·u5+2·(2·u3+3·u5) | s2^2はない |
| 5 | 2 | 5s1^2u4－3s1s2u4－5s1(2u4+u6)+s2(u4+3u6)+5u4+7u6 | s2^2はない |
| 6 | 3 | 2·s1^2·(3·u5+4·u7)-6·s1·s2·(2·u5+u7)+2·s1·(s3·(u5+2·u7)-6·u5-8·u7-4·u9)+6·s2^2·u5-2·s2·(2·s3·u5-6·u5-2·u7-3·u9)-2·(s3·(u7+2·u9)-3·u5-4·u7-5·u9) | s3^2はない |
| 7 | 3 | s1^2(7u6+9u8)－7s1s2(2u6+u8)+s1s3(3u6+5u8)－s1(9u10+2(7u6+9u8))+7s2^2u6－5s2s3u6+s2(7u10+14u6+5u8)－s3(5u10+u6+3u8)+11u10+7u6+9u8 | s3^2はない |
| 8 | 4 | 2·s1^2·(6·u11+4·u7+5·u9)-2·s1·s2·(5·u11+8·u7+10·u9)+2·s1·s3·(4·u11+8·u7+3·u9)-2·s1·s4·(3·u11+u7+2·u9)-4·s1·(6·u11+3·u13+4·u7+5·u9)+2·s2^2·(4·u7+5·u9)-8·s2·s3·(2·u7+u9)+2·s2·s4·(2·u7+3·u9)+2·s2·(4·u11+5·u13+8·u7+10·u9)+8·s3^2·u7-6·s3·s4·u7-2·s3·(3·u11+4·u13+8·u7+2·u9)+2·s4·(2·u11+3·u13+u9)+2·(6·u11+7·u13+4·u7+5·u9) | s4^2はない |
| 9 | 4 | s1^2(11u10+13u12+9u8)－s1s2(22u10+11u12+18u8)+s1s3(7u10+9(u12+2u8))－s1s4(5u10+7u12+3u8)－s1(22u10+26u12+13u14+18u8)+s2^2(11u10+9u8)－9s2s3(u10+2u8)+s2s4(7u10+5u8)+s2(22u10+9u12+11u14+18u8)+9s3^2u8－7s3s4u8－s3(5u10+7u12+9(u14+2u8))+s4(3u10+5u12+7u14+u8)+11u10+13u12+3(5u14+3u8) | s4^2はない |
| 10 | 5 | 2·s1^2·(6·u11+7·u13+8·u15+5·u9)-2·s1·s2·(12·u11+14·u13+7·u15+10·u9)+2·s1·s3·(12·u11+5·u13+2·(3·u15+5·u9))-2·s1·s4·(3·u11+4·u13+5·(u15+2·u9))+2·s1·s5·(2·u11+3·u13+4·u15+u9)-4·s1·(6·u11+7·u13+8·u15+4·u17+5·u9)+2·s2^2·(6·u11+7·u13+5·u9)-4·s2·s3·(6·u11+3·u13+5·u9)+2·s2·s4·(4·u11+5·(u13+2·u9))-2·s2·s5·(3·u11+2·(2·u13+u9))+2·s2·(12·u11+14·u13+6·u15+7·u17+10·u9)+2·s3^2·(6·u11+5·u9)-10·s3·s4·(u11+2·u9)+2·s3·s5·(4·u11+3·u9)-2·s3·(12·u11+4·u13+5·u15+2·(3·u17+5·u9))+10·s4^2·u9-8·s4·s5·u9+2·s4·(2·u11+3·u13+4·u15+5·(u17+2·u9))-2·s5·(u11+2·u13+3·u15+4·u17)+2·(6·u11+7·u13+8·u15+9·u17+5·u9) | s5^2はない |
※ 一覧表で、c=宿場数+1、cが偶数の場合、c=2s、奇数の場合は、c=2s+1、ただし、s=1、2、・・。
また、s1、s2等は、固有方程式の根（固有値）の2乗をxと置いた方程式の基本対称式を表します。
たとえば、s=2であれば、s1=x1+x2、s2=x1x2、です。
※ u1、u2等は、状態ベクトルUの要素、Uc(1)、Uc(2)等の略です。
具体的には、Uは、［U1(t),U2(t),・・,Uc(t)］（の転置）という状態ベクトル。かっこ内の数字は、日数=0、1,2、・・を表す。また、添え字の1が振り出しを、cが上がり直前にある最後の宿場を表します。
t=0のU初期状態は、［1,0,0,・・・0］（の転置）、m=0～s－1、Aをマルコフ行列とし、u1、u2等は、下図のUc（k）をukと略記したもの。ここで、c=偶数のとき、k=2m+2s-1、奇数の時、k=2m+2s、
※ cが異なるu2等は、その具体的な値（推移確率pの多項式）は、異なることに注意して下さい。
※ c=6（宿場数=5）の振り出しから、上がりまでの非対称道中双六の姿。
ここで、pは、宿場から宿場に進む確率、1-pは、宿場から前の宿場に戻る確率。
ただし、振り出しは、確率1で最初の宿場に進み、上がりからは、戻ることはありません。
このときの推移確率行列（マルコフ行列）、Aは、具体的には、下図の通りです。
目次へ戻る
「第95回第3章で、平均日数公式を構成する『新しいΨ』が基本対称式の定数項と1次項を除いて、基本対称式の2次形式であると予想した。以下では、この予想を、『（Ψは、基本対称式の）準2次形式（予想）』と呼ぶことにしよう。なお、『準』を付けた理由は、定数項と一次項を含むためだな。
さて、Ψと区別するため、基本対称式をsiとするとき、予想式、Φを次のようにおいた。
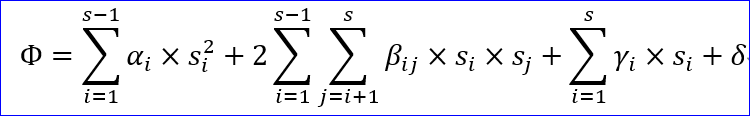
今回は、この準2次形式予想が正しいと仮定して、Φの未定係数、α、β、γ、δをどのように求めるかを考えることにしよう」
「もし、この予想が正しいとすれば、s次s変数の対称式であるΨを基本対称式に分解する手間が省けるという訳ね。その代わり、Ψ（X）=Φ（X）、ここで、Xは、xiのs次ベクトル、の関係から、s^2個のオーダーの（元数の）連立方程式を解く必要が出てくるわ」
「たしかにな。sが小さいときは、連立方程式の数が少ないので、たいしたことはないが、五十三次のs=27ともなると、かなりの手間となる。未定係数の個数を正確に計算すると、αとβが、s(s+1)/2個、γがs個、δが1個、合計して、(s+1)(s+2)/2個となる。そこで、なるべく、個々の等式、Ψ（X）=Φ（X）などにおいて、未定係数が一度に多く現れないような式の立て方を工夫したいのじゃ」
「なるほど。sに対する未定係数の個数を具体的に表すと、次表のような感じ。前回までに求めた最大のc=10は、s=5に相当するので、未定係数の個数は、21個。だから、まだ、大した数ではないけどね。
| s | 未定係数の個数 (s+1)(s+2)/2 |
| 1 | 3 |
| 2 | 6 |
| 3 | 10 |
| 4 | 15 |
| 5 | 21 |
| 6 | 28 |
| 7 | 36 |
| 8 | 45 |
| 9 | 55 |
| 10 | 66 |
| 15 | 136 |
| 20 | 231 |
| 27 | 406 |
| 30 | 496 |
「そのとおりじゃ。対称式の基本対称式への分解は、機械的とは言いながら、sが3以上になると、手作業では、やる気が起きない。そこで、DERIVEのユーザー定義関数を作って計算してきたが、sが大きくなると、DERIVEでメモリーが足りるかどうかという問題もある。
一方、『準2次形式予想』を元にした場合、そもそも、この予想が正しいのかという根本的な問題が残るが、これは、先の課題としておこう。
※ 『準2次形式予想』が一般的に成立する証明がなくても、特定のsについて、この予想を元にΨが予想式Φに等しくなる係数を決定できれば、『（対称式に関する）代数学の基本定理』により、その分解は、一意であるため、Ψの基本対称式への分解目的は、達せられる事に注意して下さい。2020/9/4注記
「では、新しい章を起こして、具体的に検討していきましょうか」
目次へ戻る
「これは、簡単ね。すべての変数、xi=0、とすれば、良いから。
すなわち、Ψ(xi=0)=Φ(xi=0)=Φ(si=0)=δ、なので、δ=Ψ(xi=0)、と求められる」
「たしかにな。定数項、δは、目の子ですぐに分かるが、後のことを考えて、別の求め方を工夫してみる。なお、HPでは、添え字が面倒なので、sk等は、sk等と書くことが多いのでご了承あれ。
それは、基本対称式、s1、s2等の相互の関係を示す、次の関数、f(t)だ。（下式は、s=2の場合）
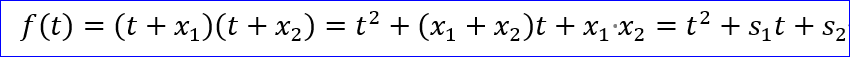
s=3以上の場合も同様の記法ができる。f(t)のtは、xと書いても良いが、個別のxiと紛らわしいので、tと書いているのじゃ。
なお、この記法は、特に目新しいものではなく、方程式の根をxiと書いたときの、f(x)=(x－x1)(x－x2)などの式とかっこ内のxiの符号が異なるだけだ。ただ、f(t)の形に書くと、t^(s-k)の係数が、skとなるため、マイナス符号を付けるか否かをsの偶奇により変える煩わしさがない。以下では、この方程式を『補助方程式』と呼ぶことにしよう。
さて、補助方程式、f(t)において、すべてのsi、i=1~s、をゼロにすると、f(t)の最高次を除くすべての係数（s1～ss）がゼロとなるので、t^s=0、となる。この解は、t=0（のs重根）となるので、－t、すなわち、すべてのxi=－0=0、とすれば、よいと分かるという考え方なのだな。
今節の最後に、Φ1=Φ－δ、ψ1=Ψ－Ψ(xi=0)、を新しく定義しておこう。
丁寧に書けば、Φ1は、
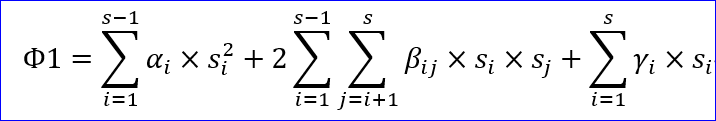
となる。
次節では、Φ1の未定係数、α、β、γについて、その求め方を考える」
目次へ戻る
「Φ1だけ見れば、未定係数α、β、γを求めるのは、簡単なように思える。Φ1をskで偏微分した後に、すべてのsi=0、とすれば、γkのみ残るので、対応する｛∂(Ψ1,sk)、xi=0｝の値が得られれば、等値することにより、γkの値が求められる。同様に2階の偏微分を利用すれば、α、βを求められる。
しかし、skは、基本対称式なのでxiの既知の関数であるが、逆にxiをskの具体的な関数で示すことは、一般には、困難。このため、∂(Ψ1,sk)の計算ができない。なぜなら、Ψ1は、xiの多項式であり、基本対称式に分解されていないからだな。ま、その分解が目的なので、できていないのは、当然だ。
そこで、∂(Ψ1,sk)=∂Ψ1/∂sk=Σ（i=1~s）（(∂Ψ1/∂xi)×(∂xi/∂sk)）、のように計算しなければならない。ところがxiは、固有方程式の固有値の2乗とした方程式の根であり、このxiをsiの関数として表すためには、s次の代数方程式の根の公式が必要となる。しかし、よく知られているように、s=5以上では、根の公式がない。従って、この方法は、実際問題として、s=1、2、程度に限定されるじゃろう」
「なるほど。s=1、2の未定係数は、s=1で、3個、s=2で、6個なので、xiとして、適当な値のセットをΦ1とΨ1の双方に代入し、等値した式を元に連立方程式を解ければ、良いので、無理に偏微分を使わなくてよさそうね」
「ともちゃんの言うとおりだ。ただ、適当な値を選ぶ際は、次の2つの注意点があるのじゃ。
1. xiとして、本来のxiの値域、0~1の実数値以外の、たとえば、整数や虚数を含めた複素数を使っても良い。
2. Φ1、Ψ1ともxiの対称式なので、xiの相互の入れ替えで同じになるXでは、新しい方程式を生み出せない。
1番目は、一般に未定係数を決めるときに使われる方法だ。2番目は、例えば、s=2の場合、［0,1］と［1,0］は、同じ等式を作るのて片方しか使えない。そこで［1,2］のような［0,1］と異なるXを与えないと異なる2つ目の式を得られない。
変数が多い場合、xiのセットとして相異なる整数の組をコンピューターで生成して与えること自体は、簡単なものの、連立方程式の係数に大きな整数が掛けられたu1、u2等が現れるだろう。このため、未定係数の個数が多い場合、それはそれで扱いが面倒になるかも知れないな」
目次へ戻る
「そこで、この小節では、k=1～sとして、ある一つの基本対称式、sk=1、とし、他の、sj=0、ここで、j<>k、となるxiの条件を求めてみよう。これは、『補助方程式』において、最高次とskを係数とするtのs－k次の項の係数を1として、他をゼロとすれば、よいので、
t^s+t^(s－k)=0、となり、t^(s－k)×(t^k+1)=0、
この解は、t=0以外は、t=（－1のk乗根）、となる。
従って、xiとしては、負号を付け、－（－1のk乗根）、残りを、ゼロとすればよい。
xj=－cos((2j+1)π/k)－#i×sin((2j+1)π/k)、j=0～k-1、ここで、#iは、虚数単位。
なお、今後、記載が面倒なので、このようなxiの集まり（ベクトル）をXkと書くことにする」
「えーと、Φ1(Xk)の値は、こうなるわね。
αの項は、k=1~s－1では、αk×(1)^2=αk、
γの項は、k=1~sで、γk×(1)=γk、
問題は、βの項ね。これは、k=sであれば、ゼロとなり、k<sの場合も
2×Σ（i=1~s-1）Σ（j=i+1~s）βij×si×sj=2×(1)Σ（j=k+1~s）βkj×sj=0、となるけど、
sj、ここで、j=k+1~s、は、仮定からゼロとなるので、結果、βの項は、現れないわ。
なので、Φ1(Xk)=αk+γk、と求められる。ただし、αkは、k=sでは、ないものとします」
「ともちゃんが計算してくれたように、Φ1(Xk)=Ψ1(Xk)、とおけば、等式は、全部でs個得られる。ただ、αがs－1個、γがs個の合計2s－1個あるため、αとγだけでも、あと、s－1個の式が必要だ。とは言え、2匹目のドジョウを狙って、sk=2、以外は、ゼロとして、同様に考えても、Xkの定数倍のベクトルが得られるだけであり、無駄じゃ」
目次へ戻る
「しかし、前小節と、skの符号を変えて、sk=－1、以外は、ゼロとすれば、状況は、変わり、独立な等式が得られる。k=1～sとして、ある一つの基本対称式、sk=－1、とし、他の、sj=0、ここで、j<>k、となるxiの条件を求めてみよう。これは、『補助方程式』において、最高次を残し、skを係数とするtのs－k次の項の係数を、－1として、他の項をゼロとすればよいので、
t^s－t^(s－k)=0、となり、t^(s－k)×(t^k－1)=0、
この解は、t=0以外は、t=（1のk乗根）、となる。
従って、xiとしては、負号を付け、－（1のk乗根）、残りを、ゼロとすればよい。
具体的には、xj=－cos(2jπ/k)－#i×sin(2jπ/k)、j=0～k-1、ここで、#iは、虚数単位。
なお、今後、記載が面倒なので、このようなxiの集まり（ベクトル）をYkと書くことにする」
「なるほど。こうすると、さらに、s個の式が手に入るわね。
えーと、Φ1(Yk)の値は、こうなるわね。
αの項は、k=1~s－1では、αk×(－1)^2=αk、
γの項は、k=1~sで、γk×(－1)=－γk、
問題は、βの項ね。これは、k=sであれば、ゼロとなり、k<sの場合も
2×Σ（i=1~s-1）Σ（j=i+1~s）βij×si×sj=2×(－1)Σ（j=k+1~s）βkj×sj=0、となるけど、
sj、ここで、j=k+1~s、は、仮定からゼロとなるので、結果、βの項は、現れないわ。
なので、Φ1(Xk)=αk－γk、と求められる。ただし、αkは、k=sでは、ないものとします」
「ここまで、くると、未定係数のαとγは、次のように求められる。
すなわち、Φ1(Xk)=αk+γk=Ψ1(Xk)、及び、Φ1(Yk)=αk－γk=Ψ1(Yk)より、
k=1~s-1において、
αk=(1/2)(Ψ1(Xk)+Ψ1(Yk))
γk=(1/2)(Ψ1(Xk)－Ψ1(Yk))
ただし、k=sでは、γs=Ψ1(Xs)、となる。
これで、残る未定係数は、βの項のみとなる。
そこで、ここまで得られたα、γを使って、新規に
Φ2=Φ1－Σ(i=1~s-1)αi×si^2－Σ(i=1~s)γi×si、
Ψ2=Ψ1－｛Σ(i=1~s-1)αi×si^2－Σ(i=1~s)γi×si、ただし、siをx1等に置き換えたもの｝、
と定義する。
Φ2は、綺麗に書けば、
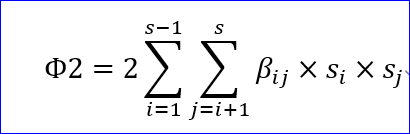
となる」
目次へ戻る
「さて、Φ2とΨ2から、βの項を求めようとして、sk以外にsj、ただし、j>k、を2つとも、その値を、例えば、1とすると、補助方程式の解が一般的には、解析的に求められなくなるのだな」
「でも、こうは、考えられないかしら。sk=sj=1、ここで、k=1~s－1、j=k+1~s、それ以外は、ゼロとしたxi（これをXk,jと書くと）、Φ2(Xk,j)の値は、仮定から、2×βkjと求められる。
一方、補助方程式の解は、数値的にしか求められないけど、その数値解を求めて、Ψ2(Xk,j)を計算して、Φ2と等値すれば、連立方程式を立てることは、できるでしょ。今までの経験から、α、β、γ、δは、整数×（u1、u2等の一次式）と予想できるので、連立方程式の係数が近似値でも、なんとかなるんじゃない？
もう少し、詳しく書くと、sk=sj=1、ここで、k=1~s-1、j=k+1~s、それ以外は、ゼロとするxiのベクトルをXk,jとする。その条件は、補助方程式において、sk=sj=1として、以外をゼロとした場合なので、
t^s+t^(s-k)+t^(s-j)=0、すなわち、k<jを考慮して、t=0以外の解は、
t^(j)+t^(j-k)+1=0、の解となる。これは、前述のように、一般には、数値解しか求められないけど、Ψ2(Xk,j)を近似的に計算することは、可能。
一方、Φ2(Xk,j)は、と言うと、（3）節のXk（sk=1、以外は、ゼロ）と同様に考えて、
βの項は、2×Σ（i=1~s-1）Σ（l=i+1~s）βij×si×sl、なんだけど、sk=1、かつ、sj=1、以外はゼロのため、
iがkの場合、2×βkj、iがjの場合は、l＞j、なので、sl=0となり、βの項は、2×βkj、となる。
従って、
Φ2(Xk,j)=2×βkj、ただし、k=1~s－1、j=k+1~s、ということになるわ」
「なるほど。シンプルで実用的な方法かもしれん。実は、次節で、Φ2、Ψ2をxk、xjにより、それぞれ、偏微分することにより、βを求めることを考えている、その方法がうまくいかない場合は、ここに戻って考えてみよう」
目次へ戻る
「①の条件を少し、緩和して、k=1~s-1、j=k+1~s、として、∂(sj,xj)=1、以外はゼロ、とするようなxiのベクトルをXj-1と書く。ただ、今のところ、（3）①、同②のように一般のsについて、｛∂(∂(Φ2,xk),xj)、Xj-1｝、を具体的に表すことが難しい。
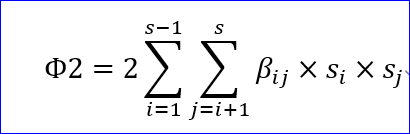
なお、ここで、Xj-1は、（3）①のXkにおいて、k=j-1とした場合で、#iは、虚数単位として、
xm=－cos((2m+1)π/(j-1))－#i×sin((2m+1)π/(j-1))、m=0～j-2、残りは、ゼロとするベクトルだ。
※補助方程式は、s-1次なので、s次ベクトル、Xj-1に1つだけ、自由度が残るが、当面、それをゼロと置く。
なお、具体的なsが与えられれば、｛∂(∂(Φ2,xk),xj)、Xj-1｝、を、すべてのk,jについて、厳密に計算することは、可能だ」
「Φ2をxkで偏微分した場合は、∂(Φ2,xk)=Σ（l=1~s）（∂(Φ2,sl)×∂(sl,xl)）、と計算するのね。さらに、xjで偏微分した結果と併せて、（Officeの数式ツールで）綺麗に書くと、下図となる。
※ Officeの数式ツールについては、『数式作成機能・ソフト』（2018年5月のご挨拶）をご参照下さい。
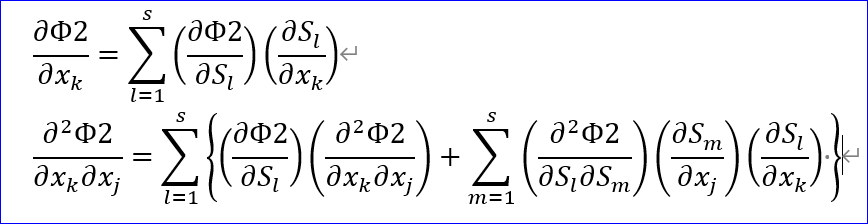
上の計算では、∂S1/∂xm=1、ここで、m=1~s、となることに注意する必要があるわ」
「その通りじゃな。最初、∂S1/∂xm=1に気がつかず、どうも計算が合わなんだ。それで、気がついた。
一方、∂Sj/∂xj=1、以外は、ゼロという条件を与える、補助方程式、
f(t)=t^2+s1t^(s-1)+s2t^(s-2)+・・・+Ss=0、において、両辺をxjで偏微分して、条件を満たすためには、
∂s1/∂xj×t^(s-1)+∂sj/∂xj×t^(s-j)=0、
t^(s-1)+t^(s-j)=0、
t^(j-1)+1=0、この解のマイナス符号を付けたものは、Xj-1、で前述のように、Xkで、k=j-1としたものと等しい。
問題は、どの程度、実用的かということだが、具体例に適用してみないと分からないことが多い。次章で、すでに基本対称式に分解済みの問題に適用してみよう」
目次へ戻る
いろいろな式や変数が出てきて、見づらくなりそうなので、データや関数等を表の形に整理しました。
c=6、宿場数が5の場合で、c=2s、と書けば、s=3の場合です。
| 変数 | 値 | 備考 |
| Ψ | (-4·u5·x1^2·x2^2·x3+6·u5·x1^2·x2^2-4·u5·x1^2·x2·x3^2+2·x1^2·x2·x3·(7·u5+2·u7)-6·x1^2·x2·(2·u5+u7)+6·u5·x1^2·x3^2-6·x1^2·x3·(2·u5+u7)+2·x1^2·(3·u5+4·u7)-4·u5·x1·x2^2·x3^2+2·x1·x2^2·x3·(7·u5+2·u7)-6·x1·x2^2·(2·u5+u7)+2·x1·x2·x3^2·(7·u5+2·u7)-4·x1·x2·x3·(9·u5+5·u7+u9)+2·x1·x2·(12·u5+10·u7+3·u9)-6·x1·x3^2·(2·u5+u7)+2·x1·x3·(12·u5+10·u7+3·u9)-4·x1·(3·u5+4·u7+2·u9)+6·u5·x2^2·x3^2-6·x2^2·x3·(2·u5+u7)+2·x2^2·(3·u5+4·u7)-6·x2·x3^2·(2·u5+u7)+2·x2·x3·(12·u5+10·u7+3·u9)-4·x2·(3·u5+4·u7+2·u9)+2·x3^2·(3·u5+4·u7)-4·x3·(3·u5+2·(2·u7+u9))+2·(3·u5+4·u7+5·u9)) | 第93回（4）のΨ×2 |
| Φ | (2·s2·s3·β↓2↓3+2·s1·s3·β↓1↓3+2·s1·s2·β↓1↓2+s2^2·α↓2+s1^2·α↓1+s3·γ↓3+s2·γ↓2+s1·γ↓1)+δ | Φ(3) |
| δ | 2·(3·u5+4·u7+5·u9) | 後述のfdelta |
この検証のため、DERIVEで、そのためのユーザー定義関数を作成しました。それが次表にまとめたものです。当面、sが10までを考えています。
| 関数・定数 | 内容 | 備考 |
| vx | [x1,x2,x3,x4,x5,x6,x7,x8,x9,x10] | ベクトル |
| vs | s個の基本対称式をベクトルに格納 変数名は、vssでs1、s2等と定義 |
Fresetでリセット |
| Freset(s) | vsなどを初期化 | 第93回で定義 |
| Φ2(n_) | 2·∑(∑(ELEMENT(β,i,j)·vss↓i·vss↓j,j,i+1,n_),i,1,n_-1) s=3の場合 (2·(s2·s3·β↓2↓3+s1·s3·β↓1↓3+s1·s2·β↓1↓2)) |
Φ2(s)を与える |
| Φ1(n_) | φ2(n_)+∑(α↓i·vss↓i^2,i,1,n_-1)+∑(γ↓i·vss↓i,i,1,n_) | Φ1(s)を与える |
| Φ(n_) | φ2(n_)+∑(α↓i·vss↓i^2,i,1,n_-1)+∑(γ↓i·vss↓i,i,1,n_)+δ s=3の場合 (2·s2·s3·β↓2↓3+2·s1·s3·β↓1↓3+2·s1·s2·β↓1↓2+s2^2·α↓2+s1^2·α↓1+s3·γ↓3+s2·γ↓2+s1·γ↓1+δ) |
Φ(s)を与える |
| fsx(f_,s) | (ITERATE([LIM(w_↓1,vss↓(w_↓2),vs↓(w_↓2)),1+w_↓2],w_,[f_,1],s))↓1 |
f_のsiをxiで置きかえる |
| ff(f_,s,k,j) | ∑(∑(∂(∂(f_,vss↓l),vss↓m)·∂(vs↓m,vx↓j)·∂(vs↓l,vx↓k),m,1,s)+∂(f_,vss↓l)·∂(∂(vs↓l,vx↓k),vx↓j),l,1,s) | f_（siの関数）の2階偏微分を与える、ただし、siは、xiの式に置き換わらずに残る |
| fdelta(Ψ_,s) | (ITERATE([LIM(w_↓1,vx↓(w_↓2),0),1+w_↓2],w_,[ψ_,1],s))↓1 | Ψ_から、δを求める |
| fpsi(Ψ_,s) | ψ_-fdelta(ψ_,s) | Ψからδを除したΨ1を与える |
| fxk(k_,s) | PROG( v_≔[0,0,0,0,0,0,0,0,0,0], w_≔VECTOR(-COS((2·j_+1)·/k_)-·SIN((2·j_+1)·/k_),j_,0,k_-1,1), u_≔VECTOR(v_↓i≔w_↓i,i,1,k_), v_) s=3の場合 ([-1/2-√3·/2,1,-1/2+√3·/2,0,0,0,0,0,0,0]) |
s(k)=1、以外はゼロとなるxiの10次元のベクトルを与える |
| fyk(k_,s) | PROG( v_≔[0,0,0,0,0,0,0,0,0,0], w_≔VECTOR(-COS((2·j_)·/k_)-·SIN((2·j_)·/k_),j_,0,k_-1,1), u_≔VECTOR(v_↓i≔w_↓i,i,1,k_), v_) s=3の場合 ([-1,1/2-√3·/2,1/2+√3·/2,0,0,0,0,0,0,0]) |
s(k)=-1、以外はゼロとなるxiの10次元ベクトル |
| falfa(f_,s) | VECTOR(1/2·(LIM(f_,[x1,x2,x3,x4,x5,x6,x7,x8,x9,x10],fxk(k_,s))+LIM(f_,[x1,x2,x3,x4,x5,x6,x7,x8,x9,x10],fyk(k_,s))),k_,1,s-1,1) s=3の場合、falfa(fsx(Φ1(3),3),3)=([α↓1,α↓2]) |
f_のsi^2の項の係数αを与える |
| fganma(f_,s) | PROG( g_≔LIM(f_,[x1,x2,x3,x4,x5,x6,x7,x8,x9,x10],fxk(s,s)), v_≔VECTOR(0,k_,1,s,1), w_≔VECTOR(1/2·(LIM(f_,[x1,x2,x3,x4,x5,x6,x7,x8,x9,x10],fxk(k_,s))-LIM(f_,[x1,x2,x3,x4,x5,x6,x7,x8,x9,x10],fyk(k_,s))),k_,1,s-1,1), u_≔VECTOR(IF(k_<s,v_↓k_≔w_↓k_,v_↓k_≔g_),k_,1,s,1), VECTOR(ELEMENT(v_,k_),k_,1,s,1)) s=3では、fganma(fsx(Φ1(3),3),3)=([γ↓1,γ↓2,γ↓3]) |
f_のsiの一次項の係数を与える |
| Fpsi2(Ψ_,s) | PROG( Freset(s), f_≔ψ_-fdelta(ψ_,s), va_≔falfa(f_,s), vga_≔fganma(f_,s), g_≔∑(va_↓i_·vss↓i_^2,i_,1,s-1)+∑(vga_↓i_·vss↓i_,i_,1,s), f_≔f_-fsx(g_,s), f_) |
ΨからΨ2を与えるδ、γ、αを計算してΨ2を求めてい |
| Fbeta(Ψ2_,s) | PROG( ma_≔VECTOR(VECTOR(LIM(∂(∂(ψ2_,vx↓j1_),vx↓k1_),[x1,x2,x3,x4,x5,x6,x7,x8,x9,x10],fxk(j1_-1,s)),j1_,k1_+1,s,1),k1_,1,s-1,1), mb_≔VECTOR(VECTOR(LIM(fsx(ff(φ2(s),s,k1_,j1_),s),[x1,x2,x3,x4,x5,x6,x7,x8,x8,x10],fxk(j1_-1)),j1_,k1_+1,s,1),k1_,1,s-1), mx_≔ma_-mb_, u1_≔[ELEMENT(mx_,1,1),ELEMENT(mx_,1,2),ELEMENT(mx_,2,1)], SOLVE(LIM(u1_,β,[0,b12,b13;0,0,b23;0,0,0]),[b12,b13,b23])) |
Ψ2からβの値を与える ただし、今回の例では、s=3に特化させている |
定数項、δは、すでに、①に掲げた表にありますように、fdelta(Ψ,3)により、簡単に計算できました。
以下では、α、γ、βの値の値を求めています。
| 変数 | 値 | 備考 |
| Φ1(3) | (2·s2·s3·β↓2↓3+2·s1·s3·β↓1↓3+2·s1·s2·β↓1↓2+s2^2·α↓2+s1^2·α↓1+s3·γ↓3+s2·γ↓2+s1·γ↓1) | Φ(3)からδを除したもの |
| Ψ1 | (-x1^2·(x2^2·(4·u5·x3-6·u5)+x2·(4·u5·x3^2-2·x3·(7·u5+2·u7)+6·(2·u5+u7))-6·u5·x3^2+6·x3·(2·u5+u7)-2·(3·u5+4·u7))-x1·(x2^2·(4·u5·x3^2-2·x3·(7·u5+2·u7)+6·(2·u5+u7))-x2·(2·x3^2·(7·u5+2·u7)-4·x3·(9·u5+5·u7+u9)+2·(12·u5+10·u7+3·u9))+6·x3^2·(2·u5+u7)-2·x3·(12·u5+10·u7+3·u9)+4·(3·u5+4·u7+2·u9))+x2^2·(6·u5·x3^2-6·x3·(2·u5+u7)+2·(3·u5+4·u7))-x2·(6·x3^2·(2·u5+u7)-2·x3·(12·u5+10·u7+3·u9)+4·(3·u5+4·u7+2·u9))+2·x3^2·(3·u5+4·u7)-4·x3·(3·u5+2·(2·u7+u9))) | fpsi1(Ψ,s) |
| α | ([2·(3·u5+4·u7),6·u5]) | falfa(Ψ1,3) |
| γ | ([-4·(3·u5+2·(2·u7+u9)),2·(6·u5+2·u7+3·u9),-2·(u7+2·u9)]) | fganma(Ψ1,3) |
| Ψ2 | (-2·(x1^2·(2·u5·x2^2·x3+x2·(2·u5·x3^2-x3·(u5+2·u7)+3·(2·u5+u7))+3·x3·(2·u5+u7))+x1·(x2^2·(2·u5·x3^2-x3·(u5+2·u7)+3·(2·u5+u7))+x2·x3·(9·(2·u5+u7)-x3·(u5+2·u7))+3·x3^2·(2·u5+u7))+3·x2·x3·(x2+x3)·(2·u5+u7))) | Fpsi2(Ψ,3) |
| β | ([b12=-3·(2·u5+u7)∧b13=u5+2·u7∧b23=-2·u5]) | β1,2等をb12として計算 |
| Ψ | (2·s1^2·(3·u5+4·u7)-s1·(6·s2·(2·u5+u7)-2·s3·(u5+2·u7)+4·(3·u5+2·(2·u7+u9)))+6·s2^2·u5+s2·(2·(6·u5+2·u7+3·u9)-4·s3·u5)-2·s3·(u7+2·u9)+2·(3·u5+4·u7+5·u9)) =(-4·u5·x1^2·x2^2·x3+6·u5·x1^2·x2^2-4·u5·x1^2·x2·x3^2+2·x1^2·x2·x3·(7·u5+2·u7)-6·x1^2·x2·(2·u5+u7)+6·u5·x1^2·x3^2-6·x1^2·x3·(2·u5+u7)+2·x1^2·(3·u5+4·u7)-4·u5·x1·x2^2·x3^2+2·x1·x2^2·x3·(7·u5+2·u7)-6·x1·x2^2·(2·u5+u7)+2·x1·x2·x3^2·(7·u5+2·u7)-4·x1·x2·x3·(9·u5+5·u7+u9)+2·x1·x2·(12·u5+10·u7+3·u9)-6·x1·x3^2·(2·u5+u7)+2·x1·x3·(12·u5+10·u7+3·u9)-4·x1·(3·u5+2·(2·u7+u9))+6·u5·x2^2·x3^2-6·x2^2·x3·(2·u5+u7)+2·x2^2·(3·u5+4·u7)-6·x2·x3^2·(2·u5+u7)+2·x2·x3·(12·u5+10·u7+3·u9)-4·x2·(3·u5+2·(2·u7+u9))+2·x3^2·(3·u5+4·u7)-4·x3·(3·u5+2·(2·u7+u9))+2·(3·u5+4·u7+5·u9)) |
Φ(3)に各係数を当てはめたもの（検算用） |
検算した結果を①のΨと（差し引きして）比較するとゼロとなり、正しく、準2次形式の係数が求められていることが分かりました。
今回は、βの求め方が洗練されていないため、s=4～5の既知の例やs>5の未知の例に関しての計算は、次回にまわすことにしました。
目次へ戻る
c=6（s=3）のΨは、次のようにu5等でくくることで、くくられた多項式は、それぞれ、基本対称式siの多項式です。これをΨのuk分解と呼んでおきましょう。なお、基本対称式に分解する前の、u5等でくくられた多項式は、xiの多項式ですが、次節で述べるように、個別に基本対称式に分解できます。
| 項目 | 値 |
| Ψ | 2·s1^2·(3·u5+4·u7)-6·s1·s2·(2·u5+u7)+2·s1·(s3·(u5+2·u7)-6·u5-8·u7-4·u9)+6·s2^2·u5-2·s2·(2·s3·u5-6·u5-2·u7-3·u9)-2·(s3·(u7+2·u9)-3·u5-4·u7-5·u9) |
| u5の項 | (6·s1^2-12·s1·s2+2·s1·s3-12·s1+6·s2^2-4·s2·s3+12·s2+6) |
| u7の項 | (8·s1^2-6·s1·s2+4·s1·s3-16·s1+4·s2-2·s3+8) |
| u9の項 | (-8·s1+6·s2-4·s3+10) |
第93回の『マルコフ過程（6）（非対称型道中双六：平均日数と対称式）』において、気がつくべきでしたが、対称式の基本対称式への分解に気を取られ過ぎて、足下にあった、もう一つの重要な点（uk分解）を見落としていました。
すなわち、1.（2）のΨをsiの多項式で表した表を眺めると、Ψ=Σuk×Fk（siの多項式=xiの多項式）、と書けることに気がつきます。ここで、ukは、最後の宿場の状態ベクトルのt=k時の値で、t=c－1から、1つ飛びにs個です。
なお、Fkは、si（i=1～s）のみの多項式で、uk等を含みません。そして、次の重要な点があります。
1. Fkは、それぞれ、対称式であり、個別に基本対称式に分解できる、
2. Ψで『準2次形式』予想が成立すれば、Fkもそれぞれ準2次形式である、
これらは、ukの独立性から、容易に分かります。
uk分解の利点は、ウェアリングの方法や準2次形式予想を元に、対称式を基本対称式に分解する際、Ψをs個に分解して、実行できるので、sが大きい場合、手数やメモリーを節約できます。
平均日数公式において、di等をクラメルの公式で、ukとxiの式で表して、平均日数計算公式に代入した姿から、Σuk×（xiの有理式）と書けることが分かります。ただし、有理式は、具体的なsについては、xiの多項式になりますが、一般的に表すことができていません。今後、もう少し、時間が必要です。
目次へ戻る
作成日：2020/9/3
1.（3）に準2次形式予想とΨの基本対称式分解の注記：2020/9/4
1.（2）に説明図とマルコフ行列の図を追加：2020/9/5
4.Ψのuk分解を追記：2020/9/13
4.の文言を微修正：2020/9/14
「概2次形式」を「準2次形式」と呼称を変更：2021/1/1
