数式処理ソフト DERIVE(デライブ) de ドライブ
75.多角形及び多面体の重心と高次のモーメント(1)
目次
(1)はじめに
(2)多角形の重心及び高次のモーメント(2次元空間)
(3)多角形の重心(3次元空間)
(4)回転行列(2次元空間)
(5)多角形の重心(3次元空間の特殊な場合)
(6)回転行列(3次元空間)
(7)多角錘の重心
(8)多角形の面積と重心を求めるExcelブック (2015/10/10 追記)
(1)はじめに
「宿題を片付けようシリーズの第2弾じゃ。
第61回「多面体の体積公式」では、3次元空間上の多面体の体積を求める公式を導いた。
また、以前に、第39回「3次元空間における平面上の多角形の面積」で多角形の面積を表す公式を扱った。
さらに、だいぶ、前になるんじゃが、「今月のご挨拶」の2002年3月「図形の面積と重心」では、平面上の多角形の面積、重心及び高次のモーメントを表す式を扱ったんじゃったな」
 「そうだったわね。
「そうだったわね。
なつかしいな。
そして、今回は、2015年2月の「今月のご挨拶」「宿題を片付けよう!?」に掲げた第16番目の問題というわけね」
「ともちゃんかい。毎回、ご苦労様じゃのう。
今年は、立秋を過ぎたと思うたら、急に涼しくなって、わしも驚いたぞ。
ま、涼しいのは、ありがたいがの、急に気候が変わるのは、困る気もする」
「たしかにね。
お年寄りや赤ちゃんなどは、気温の変化についてこれないこともあるから、おじいさんも気をつけて下さいな」
「やれやれ、年をとるのは、ホント大変なことじゃな。
さて、次節では、平面上の多角形の重心及び高次のモーメントを求めることから始めようかの」
目次へ戻る
(2)多角形の重心及び高次のモーメント(2次元空間)
 「多角形の場合は、2002年3月に、平面上のストークスの定理から、
「多角形の場合は、2002年3月に、平面上のストークスの定理から、
∫∫(x^k×y^m)dxdy=(1/(k+m+2))(∫(x^(k+1)y^m)dy-∫(x^k y^(m+1))dx)、を説明しているわね。
ここで、k、mは、ゼロ以上の整数とする。
また、右辺の積分は、多角形の上から見て反時計回りに行う接線線積分を表します」
「そうじゃな。
2002年3月の記事では、ごく簡単にしか説明していないがの。
「面積」については、前節で引用している第39回では、ストークスの定理から導く方法についても、かなり丁寧に扱っておる」
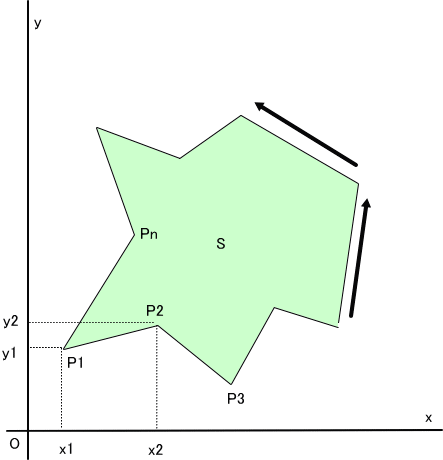
「図で説明するよ。
分かりやすくするために、2次元平面上の多角形を考えて、多角形Sの頂点を反時計回りに、P1~Pnとする。
また、各点の座標値を[x(i),y(i)]、i=1~n。(xi のように下付添え字で書きたいけど、面倒なので、x(i)のように書くわよ。
さてと、3次元空間上の面に対するストークスの定理は、∫∫▽×A・dS=∫A・dt、だったでしょ。
▽は、rot または curl とも書かれる演算子で、(∂/∂x,∂/∂y,∂/∂z)、×は、ベクトルの外積、・は、ベクトルの内積を、dSは、面の法線ベクトル、dtは、接線ベクトルを示します。
DERIVEでは、rot という関数はなくて、curl なのよ。(前にも言ったわね)
さて、面積を求める場合は、ベクトル点関数Aを[-y,x,0]と置けば、▽×A=[0,0,2]となるので、
∫∫▽×A・dS=∫∫2dxdy=2S、ここで、Sは、多角形の面積。
一方、右辺の接線線積分はというと、dt=[dx,dy,0]と考えて、∫A・dt=∫(-y dx+x dy)、なんだけど、
多角形では、dx=x(i+1)-x(i)、dy=y(i+1)-y(i)、また、∫をΣに置き換えて、
∫(-y dx+x dy)=Σ(i=1~n)(-y(i)(x(i+1)-x(i))+x(i)(y(i+1)-y(i))=Σ(-y(i)x(i+1)+x(i)y(i+1))、
となり、
2S=Σ(i=1~n)(-y(i)x(i+1)+x(i)y(i+1))、と(倍)面積が求められる。
なお、x(n+1)、y(n+1)は、x(1)、y(1)を意味します」
「うん、だいたい、そういう流れじゃったな。
面積については、各点の位置ベクトルをr(i)で表したとき、2S=ABS(r(i)×r(i+1))という簡潔な表現もすでに紹介している。
この表現ならば、3次元空間上の多角形の面積についても、そのまま通用することは、第39回で説明した。
さて、面積の式の導出なんじゃが、線積分、∫x dy などをΣx(i)(y(i+1)-y(i))と置くのは、正しいんじゃが、重心などの場合は、異なることに注意じゃ。
今、ベクトル点関数をA=[-(y^(m+1)(x^k),(x^(k+1)(y^m),0]、ここで、k、mは、ゼロまたは正の整数。
rot(A)(=Curl(A))=[0,0,(k+m+2)(x^k)(y^m)]、となるので、
(k+m+2)∫∫(x^k)(y^m)dxdy=∫-(y^(m+1)(x^k))dx+∫x^(k+1)(y^m))dy、と表せる。
重心のX座標(Gx)であれば、Gx=∫∫xdxdy/S、で求められる。(Sは多角形の面積)
ただし、多角形の厚さはその大きさに比較して薄く、かつ、質量の面密度は、一様とするのは、言うまでもないがの。
k=1、m=0とおき、∫∫x dxdy=(1/3)(∫-y x dx +∫x^2 dy)、
さて、右辺の線積分を計算するために、たとえば、点 P1とP2の間では、
x=(x(2)-x(1))p+x(1)、
y=(y(2)-y(1))p+y(1)、
ただし、p=0~1のパラメータと置く。
右辺の第1項の積分記号内は、、-y x dx =-((x(2)-x(1))p+x(1))((y(2)-y(1))p+y(1))(x(2)-x(1))dp、と表せる。
実際に点 P1とP2の間で計算すると、(x(1) - x(2))(x(1)(2y(1) + y(2)) + x(2)(y(1) + 2y(2)))/6、
同様に、右辺第2項の積分記号内は、x^2 dy=((x(2)-x(1))p+x(1))^2(y(2)-y(1))dp、となるので、
点 P1とP2の間で計算すると、((x(1)^2 + x(1)x(2) + x(2)^2)(y(2)- y(1))/3)、
両者合計し、(1/3)をかけると、(1/6)((x(1) + x(2))(x(1)y(2) - x(2)y(1))、
従って、1をi、2をi+1と置き換えて、Σをとると、重心のx座標が、
Gx=(1/6S)Σ(i=1~n)((x(i) + x(i+1))(x(i)y(i+1) - x(i+1)y(i))、と頂点の座標値のみで求められる」
「えーと、私からも注意なんだけど、2002年3月の記事では、多角形を時計回りに回って計算するように書いているの。
そのため、上のGxの式と比較して、x(i)y(i+1) - x(i+1)y(i) の順番が逆になっています。
ここでは、反時計回りに回っているとして、計算しているからね。
同様に、y方向の重心位置 Gyを計算すると、k=0、m=1 から、
∫∫y dxdy=(1/3)(∫-y ^2 dx +∫xy dy)=(1/6)Σ(i=1~n)(y(i)+y(i+1))(x(i)y(i+1)-x(i+1)y(i))、
よって、Gy=(1/6S)Σ(i=1~n)(y(i)+y(i+1))(x(i)y(i+1)-x(i+1)y(i))、と求められる」
「よっしゃ。
面積は、スカラー量なので、座標の取り方には、無関係じゃ。
一方、重心は、ベクトル量となるので、座標の平行移動や回転で、頂点の位置ベクトルと同等の変換を受ける。
では、次に2次のモーメントを求めてみよう。
力学では、慣性モーメントと言われる量になる。
先に仮定したように面が薄く、かつ、質量の面密度が一定とする。
多角形のx軸の周りの慣性モーメント Mxx=∫∫y^2 dxdy などと表される。
これは、k=0、m=2、の場合なので、∫∫y^2 dxdy =(1/4)∫x y^2 dy- y^3 dx、
重心の場合と同様に計算すると、Mxx=(1/4)Σ((y(i)^2 + y(i)y(i+1) + y(i+1)^2)(x(i)y(i+1)
- x(i+1)y(i))/3)、と求められることが分かる。
簡単な例で検算してみよう。
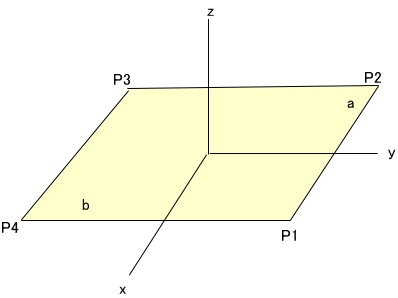
上図のような長方形の薄い板がある。座標の原点を長方形の中心に置いたとき、x軸方向の長さをa、y軸方向の長さをbとして、
x軸の周りの慣性モーメントを求めてご覧」
「Mxx=(1/4)Σ((y(i)^2 + y(i)y(i+1) + y(i+1)^2)(x(i)y(i+1) - x(i+1)y(i))/3)、なんだけど、
P1は、[a/2,b/2]、以下、P2 [-a/2,b/2]、P3 [-a/2,-b/2]、P4 [a/2,-b/2]、
よって、Mxx=ab^3/12、となる。薄い板の質量M=abを使えば、Mxx=Mb^2/12、力学の教科書に出てくる式※に一致するわ。
※「力学」(原島鮮:裳華房:昭和45年増補第21版)の161ページ」
「まあ、この例では、定義式から計算した方が早いが、図形が少し複雑な場合は、大変じゃ。
なお、対称性から、Myy=Ma^2/12、
また、z軸の周りの慣性モーメントMzz=Mxx+Myy、であるので、Mzz=M(a^2+b^2)/12 じゃ」
「えーと。
最後のところを注釈します。Mzz=Mxx+My y のところね。
薄い板の場合は、Mzz=∫r^2dxdy、ここで、rは、z軸からの距離とすると、
r^2=x^2+y^2、なので、Mz=∫r^2dxdy=∫x^2dxdy+∫y^2dxdy=Myy+Mxx、となるためなのね。
これは、原島先生の本の160ページに説明されています」
「ありがとさん。
Mzz=Mxx+Myyの関係は、長方形に限らず、薄い板と見なせる場合には、成り立つのじゃ。
重心は、ベクトル量じゃったが、慣性モーメントはというと、慣性テンソル(平面の場合は2行2列、3次元では3行3列の行列)で表される。
例題の長方形では、座標の原点及び軸を長方形の主軸にとっているので、慣性テンソルは、MxxとMyyが正で、MxyやMyxは、ゼロとなる。
実際、Mxy=Myx=∫xy dxdy は、対称性から考えて、ゼロとなる。
ま、慣性テンソルについては、ここでは、これ以上触れないことにしよう。
次節では、3次元空間上の多角形の重心について考えてみよう」
----------------------------------------------
∫∫x^k y^m dx dy=(1/(k+m+2))(∫-(y^(m+1)(x^k))dx+∫x^(k+1)(y^m))dy) の計算(補足)
点P1とP2の間で考える。
x=(x(2)-x(1))p+x(1)、
y=(y(2)-y(1))p+y(1)、
ただし、p=0~1のパラメータと置く。
第1項の定積分は、P1とP2の間で、∫-(βp+b)^(m+1) (αp+a)^k αdp、と書ける。
ここで、α=x(2)-x(1)、β=y(2)-y(1)、a=x(1)、b=y(1)、である。
また、第2項は、∫(αp+a)^(k+1) (βp+b)^m βdp、と書ける。
従って、両者の計は、∫((a + pα)^k(b + pβ)^m(aβ - bα))dp、となる。(k+m+2)で除し、k=0~3、を計算し、下記の表にまとめた。
kを指定すると、一般のmについて表式が得られるが煩雑なため、m=0~3について示した。
なお、表では、α、β、a、bを元に戻し、x(1)をx1、などと表している。また、変数間の・は、乗算を表すDERIVEの記号で、内積記号ではない。
| |
m=0 |
m=1 |
m=2 |
m=3 |
| k=0 |
((x1·y2 - x2·y1)/2) |
((y1 + y2)·(x1·y2 - x2·y1)/6) |
((y1^2 + y1·y2 + y2^2)·(x1·y2 - x2·y1)/12) |
((y1^3 + y1^2·y2 + y1·y2^2 + y2^3)·(x1·y2 - x2·y1)/20) |
| k=1 |
((x1 + x2)·(x1·y2 - x2·y1)/6) |
((x1·y2 - x2·y1)·(x1·(2·y1 + y2) + x2·(y1 + 2·y2))/24) |
((x1·y2 - x2·y1)·(x1·(3·y1^2 + 2·y1·y2 + y2^2) + x2·(y1^2 + 2·y1·y2 + 3·y2^2))/60) |
((x1·y2 - x2·y1)·(x1·(4·y1^3 + 3·y1^2·y2 + 2·y1·y2^2 + y2^3) + x2·(y1^3
+ 2·y1^2·y2 + 3·y1·y2^2 + 4·y2^3))/120) |
| k=2 |
((x1^2 + x1·x2 + x2^2)·(x1·y2 - x2·y1)/12) |
((x1·y2 - x2·y1)·(x1^2·(3·y1 + y2) + 2·x1·x2·(y1 + y2) + x2^2·(y1 + 3·y2))/60) |
((x1·y2 - x2·y1)·(x1^2·(6·y1^2 + 3·y1·y2 + y2^2) + x1·x2·(3·y1^2 + 4·y1·y2
+ 3·y2^2) + x2^2·(y1^2 + 3·y1·y2 + 6·y2^2))/180) |
((x1·y2 - x2·y1)·(x1^2·(10·y1^3 + 6·y1^2·y2 + 3·y1·y2^2 + y2^3) + 2·x1·x2·(2·y1^3
+ 3·y1^2·y2 + 3·y1·y2^2 + 2·y2^3) + x2^2·(y1^3 + 3·y1^2·y2 + 6·y1·y2^2
+ 10·y2^3))/420) |
| k=3 |
((x1^3 + x1^2·x2 + x1·x2^2 + x2^3)·(x1·y2 - x2·y1)/20) |
((x1·y2 - x2·y1)·(x1^3·(4·y1 + y2) + x1^2·x2·(3·y1 + 2·y2) + x1·x2^2·(2·y1
+ 3·y2) + x2^3·(y1 + 4·y2))/120) |
((x1·y2 - x2·y1)·(x1^3·(10·y1^2 + 4·y1·y2 + y2^2) + 3·x1^2·x2·(2·y1^2 +
2·y1·y2 + y2^2) + 3·x1·x2^2·(y1^2 + 2·y1·y2 + 2·y2^2) + x2^3·(y1^2 + 4·y1·y2
+ 10·y2^2))/420) |
((x1·y2 - x2·y1)·(x1^3·(20·y1^3 + 10·y1^2·y2 + 4·y1·y2^2 + y2^3) + x1^2·x2·(10·y1^3
+ 12·y1^2·y2 + 9·y1·y2^2 + 4·y2^3) + x1·x2^2·(4·y1^3 + 9·y1^2·y2 + 12·y1·y2^2
+ 10·y2^3) + x2^3·(y1^3 + 4·y1^2·y2 + 10·y1·y2^2 + 20·y2^3))/1120) |
上記表を元に多角形全体で計算するには、x1をx(i)、x2をx(i+1)、y1をy(i)、y2をy(i+1)に置き換えて、i=1~n(頂点の総数)について和をとればよい。
目次へ戻る
(3)多角形の重心(3次元空間)
「3次元空間上の多角形の面積 S については、第39回で詳しく述べているとおりじゃ」
 「それが、2S=ABS(Σ(r(i)×r(i+1)))ね。
「それが、2S=ABS(Σ(r(i)×r(i+1)))ね。
ただし、r(i)は、多角形の頂点の3次元位置ベクトルで、多角形を外から見て反時計回りに番号を振ったものよ」
「2次元空間では、(z成分のみを考えるので)絶対値 ABS( )をとるのは、番号の振り方が逆回りでも面積が正とするためじゃ。
3次元空間では、3次元のベクトル量なので、必ず絶対値をとる必要がある」
「そこで、多角形の重心なんだけど、第2節では、重心G(Gx,Gy)として、
Gx=(1/6S)Σ(i=1~n)((x(i) + x(i+1))(x(i)y(i+1) - x(i+1)y(i))、
Gy=(1/6S)Σ(i=1~n)(y(i)+y(i+1))(x(i)y(i+1)-x(i+1)y(i))、と表しているんだけど、
これは、多角形と同一平面上の座標原点・軸から見た頂点の位置を元にした計算式よね。
こいつを3次元空間で考える必要があるんだけど、面積の場合のようには、いかないわ」
「下図で考えてみよう。
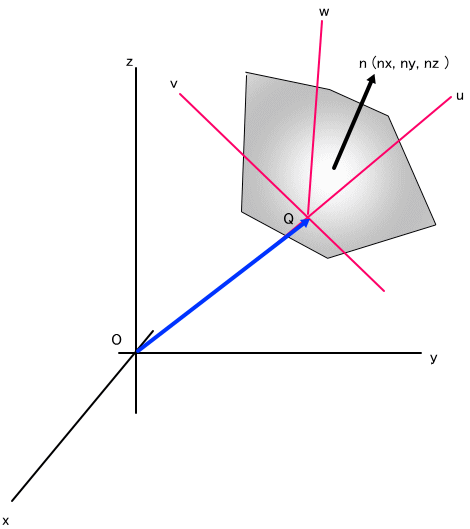
今、上の図のように3次元空間上に多角形がある。
各頂点の3次元空間のxyz座標系で表した位置ベクトルをr(i)などとする。
ここでは、上図のように、面法線ベクトルn(nx,ny,nz)が向く方向を表として頂点の番号を振ったものとする。
すなわち、nは、Σr(i)×r(i+1)と同一方向となる。
ここで、重心 G として、xyz座標系における値 OG=[Gx,Gy,Gz]を求めたいわけじゃ。
分かっているのは、多角形と同一平面上の座標原点・軸で考えた時の頂点の座標値(u(i),v(i),w(i))を元にした場合の計算式じゃ。
ただし、w(i)は、すべてゼロじゃがの。
それは、QG=[Gu,Gv,Gw]と書くと、
Gu=(1/6S)Σ((u(i) + u(i+1))(u(i)v(i+1) - u(i+1)v(i))、
Gv=(1/6S)Σ(v(i)+v(i+1))(u(i)v(i+1)-u(i+1)v(i))、
Gw=0、
となるというのが、前節の結果じゃった。
そこで、まずは、多角形上のuvw座標系と外部のxyz座標系との関係を与えることが必要じゃ」
「となると、多角形と同一平面上の任意のQを原点として、xyz座標系から見たQの位置ベクトルをOQ=[Qx,Qy,Qz]とするでしょ。
次に、xyz座標系から見た任意の点の位置ベクトルをr、同じ点をuvw座標から見た位置ベクトルを Rとする。
今、xyz座標系の座標軸の方向をすべて保ったまま、原点をOからQに移動した座標系XYZを考えたとき、
x=X+Qx、などとなる。
一方、uvw座標系は、XYZ座標系を、回転したものである。
回転に伴う変換行列をTで表すと、R=[X,Y,Z]T、である。
従って、R=(r-OQ)T、となる」
「それでは、回転行列 Tを具体的に求めることを考えてみよう。
回転行列については、以前にも出てきたんじゃが、2次元の場合が中心だったので、次節であらためて検討しよう」
目次へ戻る
(4)回転行列(2次元空間)
「まずは、2次元の場合について、下図で考えてみよう。
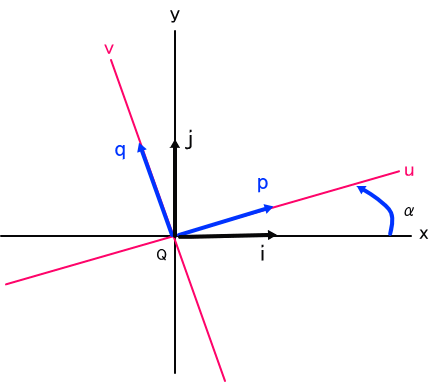
上の図では、xy座標系とuv座標系と共通の原点Qを描いてある。
傾けた角度は、図のように、αとする。(変域は、-π~π)
このとき、xy系の単位ベクトルをi,j、uv系の単位ベクトルをp,qとしたとき、お互いの関係を表す式を導いてご覧」
 「これは、簡単。
「これは、簡単。
i=p cos(α)-q sin(α)、
j=p sin(α)+q cos(α)でしょ」
「うん、それで、正しいんじゃが、コサイン関数だけで書いてみたらどうなるじゃろう」
「えーとね、
i=p cos(α)+q cos(π/2+α)、
j=p cos(π/2-α)+q cos(α)、かな」
「そうじゃのう。
これ、すなわち、「方向余弦」による表現というわけじゃ。
一般に、
i=p cosθ(u:x)+q cosθ(v:x)、
j=p cosθ(u:y)+q cosθ(v:y)、
ここで、θ(u:x)などは、x軸とu軸との間の角度じゃ。
なお、角度は、2つあるが、π以下の大きさの角度を利用する」
「なるほど。
とすると、2次元空間上の任意の点の位置ベクトルを r としたとき、原点は、同一なので、
r=x i +y j=u p+v q、ここで、x、yは、rのxy座標系における座標値、u,vは、uv座標系の座標値とする。
よって、
r=x(p cosθ(u:x)+q cosθ(v:x))+y(p cosθ(u:y)+q cosθ(v:y))、
=(x cosθ(u:x)+y cosθ(u:y))p+(x cosθ(v:x)+y cosθ(v:y))q、
この関係を整理すると、
[u,v]=[x,y]×T、
ここで、Tは、T=[[cosθ(u:x),cosθ(v:x)],[cosθ(u:y), cosθ(v:y)]]、
という2行2列の行列となる訳ね。
Tの要素は、4つあるんだけど、独立なのは、1つだけ。
なぜかっていうと、iとjの大きさが1であることから、
i・i=1=(p cosθ(u:x)+q cosθ(v:x))・(p cosθ(u:x)+q cosθ(v:x))
=(cosθ(u:x))^2+(cosθ(v:x))^2、
また、
j・j=1=(p cosθ(u:y)+q cosθ(v:y))・(p cosθ(u:y)+q cosθ(v:y))
=(cosθ(u:y))^2+(cosθ(v:y))^2、
ここで、・ は、ベクトルの内積を表すものとする。
さらに、iとjは、直交するため、i・j=0 より、
cosθ(u:x)cosθ(u:y)+cosθ(v:x)cosθ(v:y)=0、
以上の3つの式より、連立方程式を解くと、θ(u:x)=αとして、トリビアルな解を除いて、
cosθ(v:x)=sin(α)、cosθ(u:y)=sin(α)、 cosθ(v:y)=-cos(α)、
または、
cosθ(v:x)=sin(α)、cosθ(u:y)=-sin(α)、 cosθ(v:y)=cos(α)、
または、
cosθ(v:x)=-sin(α)、cosθ(u:y)=sin(α)、 cosθ(v:y)=cos(α)、
または、
cosθ(v:x)=-sin(α)、cosθ(u:y)=-sin(α)、 cosθ(v:y)=-cos(α)、
の4組の解が得られる。
しかし、青色で示した1番目と4番目の解は、α=0のときの結果を調べると、
[u,v]=[x,-y]、となり、正しくないことが分かる。
また、2番目で、αを-αとすれば、3番目のものと一致することが分かるので、図に合わせると、
cosθ(v:x)=-sin(α)、cosθ(u:y)=sin(α)、 cosθ(v:y)=cos(α)
を唯一の解として良い」
「Tの要素は、4つあったが、条件式が3つあったため、独立な変数は、1つだけとなったのじゃな。
[u,v]=[x,y][[cos(α),-sin(α)],
sin(α),cos(α)]]、
Tの逆行列は、Tの転置行列であるので、
[x,y]=[u,v][[cos(α),sin(α)],
-sin(α),cos(α)]]、
とも書ける」
「逆行列が転置行列になるのは、どんな時だっけ?」
「逆行列が存在するのは、行列式がゼロとならない正則行列の場合じゃ。
そして、すべての要素が実数の直交行列の逆行列は、転置行列となる」
「えーと、直交行列ってのは?」
「行列の各行(各列)の自身への内積が1であり、異なる行(列)同士の内積が0となるような行列じゃな。
そして、今回のような回転による変換は、「直交変換」と呼ばれる。
さて、次節では、重心について、回転行列を使った方法を調べて見よう」
目次へ戻る
(5)多角形の重心(3次元空間の特殊な場合)
「まずは、図を見て欲しいんじゃがな。
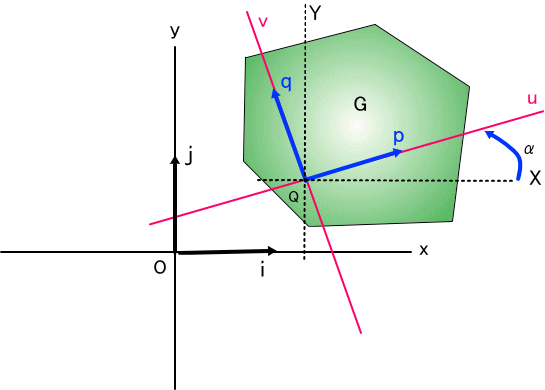
上の図に緑色の多角形が描かれておる。
基本となるのは、xyz座標系じゃ。図は、z軸の直上から見下ろしている状態じゃ。uv平面は、xy平面と同一面上にあるとする。(Qz=0)
多角形上の点 Qを原点とするuvw座標系がある。w軸は、z軸に平行だ。
uvw座標系は、xyz座標系を平行移動したXYZ座標系から見て、Qの回りに角度αだけ回転している。
このとき、(3)節でともちゃんが示してくれたように、任意の点のxyz座標系から見た位置ベクトルをr 、uvw座標系から見た位置ベクトルをRとしたとき、
R=(r-OQ)T、の関係がある。これは、r=R T'+OQとも書ける。(T'は、Tの転置行列)
ここで、R=[u,v,w]、r=[x,y,z]、OQ=[Qx,Qy,0]、
また、T=[[cos(α),-sin(α),0],[sin(α),cos(α),0],[0,0,1]]、である。(3次元ということで3行3列の行列)
さて、面積は、どうなるるかの?」
 「そうね。
「そうね。
面積は、多角形上のP1、P2という隣り合う2つの点の頂点を考えて、
xyz座標系で、 r1=[x1,y1,0]、r2=[x2,y2,0]、
uvw座標系では、R1=[u1,v1,0]、R2=[u2,v2,0]、とすると、
R1×R2=((r1-OQ)T)×((r2-OQ)T)=[0,0,Qx(y1-y2)+Qy(x2-x1)+x1y2-x2y1]、となる。
しかし、z成分の第1項と第2項は、x1をx(i)、x2をx(i+1)等に置き換えて、Σをとると、ゼロになってしまう。
従って、第3項の、Σ(x(i)y(i+1)-x(i+1)y(i))が残る。
一方、これは、直接、Σr(i)×r(i+1)、と計算したベクトルのz成分と同じとなり、倍面積を与えている」
「なるほど。
当然ながら、面積は、座標系の取り方に依存しないことが確認できたな。
じゃ、わしが重心の場合をやってみよう。
(1)α=0、すなわち、u軸、v軸も傾いていない場合。
uvw系の重心の表現をP1とP2の間で見ると、
Gu:(1/6S)((u(1) + u(2))(u(1)v(2) - u(2)v(1))、
Gv:(1/6S)(v(1)+v(2))(u(1)v(2)-u(2)v(1))、
Gw:0、
u1=x1-Qx、v1=y1-Qy、
u2=x2-Qx、v2=y2-Qy、
から、((u(1) + u(2))(u(1)v(2) - u(2)v(1))
=2qx^2(y2-y1) + 2qxqy(x1 - x2) + qx(x1(y1 - 3y2) + x2(3y1 - y2)) + qy(x1 + x2)(x2 - x1) + (x1 + x2)(x1y2 - x2y1)、
となる。(qx等は、Qxと同一)
第1項:2qx^2(y2-y1) は、Σをとると、互いに打ち消し合うので、ゼロとなる。
第2項:2qxqy(x1 - x2) も、Σをとると、同様にゼロとなる。
第3項:qx(x1(y1 - 3y2) + x2(3y1 - y2)) =Qx(x1y1-x2y2)-3Qx(x1y2-x2y1)は、Σをとると、-3Qx×2S=-6S×Qx、となる。(Sは面積)
第4項:qy(x1 + x2)(x2 - x1) =Qy(x2^2-x1^2)は、Σをとると、ゼロになる。
第5項:(x1 + x2)(x1y2 - x2y1)は、Σをとると、6S×Gx である。
従って、Gu=(1/6S)Σ((u(i) + u(i+1))(u(i)v(i+1) - u(i+1)v(i))=Gx-Qx、となることが分かる。
ところで、これは、QG=OG-OQ、から得られるものと同一である。
Gvについても、Gv=Gy-Qyと同様の結果となる」
「じゃ、わたしは、DERIVEで確認してみるよ。
最初に、オプションメニューの「モード設定」の入力タブで「連続した文字列を1変数と見なす」を選択する。
InputMode := Word、と表示される。このモードでは、大文字と小文字は区別されない。
従って、x2 と x*2 とは、別とみなされるの。このように、積は、意識して「*」で明示するようにする必要があるわよ。
一方、何も宣言しないときは、「1文字は1変数と見なす(InputMode:= Character)」となっているから、x2は、x*2と同一視される。
さて、4つのベクトルを、
x:=[x1, x2, x3, x4, x5, x6, x7, x8, x9, x10]、
y:= [y1, y2, y3, y4, y5, y6, y7, y8, y9, y10]、
u:= [u1, u2, u3, u4, u5, u6, u7, u8, u9, u10]、
v:=[v1, v2, v3, v4, v5, v6, v7, v8, v9, v10,]、
と頂点数が10個まで多角形に対応できるように、値を代入する。
DERIVEで実際に使用する際は、k番目の要素を x↓k のように書くと、xk とみなされる。
u↓k:= x↓k - Qx、v↓k:= y↓k - Qy、と定義して、解析メニューから数列の作成で、VECTOR(u↓k ≔ x↓k -
qx, k, 1, 10, 1)、のように値を計算する。
vについても同様に、VECTOR(v↓k ≔ y↓k - qy, k, 1, 10, 1)、と計算する。
また、関数として、
面積 S(n):=(1/2){ ∑(x↓j·y↓(j + 1) - x↓(j + 1)y↓j, j, 1, n - 1) + (x↓n·y↓1
- x↓1·y↓n)}、
重心の位置ベクトル、QG=[Gu,Gv]、OG=[Gx,Gy] として、
Gx(n):=(1/6S(n)){(∑((x↓j + x↓(j + 1))·(x↓j·y↓(j + 1) - x↓(j + 1)·y↓j),
j, 1, n - 1) + (x↓n + x↓1)·(x↓n·y↓1 - x↓1·y↓n))}、
Gu(n):=(1/6S(n)){∑((u↓j + u↓(j + 1))·(u↓j·v↓(j + 1) - u↓(j + 1)·v↓j),
j, 1, n - 1) + (u↓n + u↓1)·(u↓n·v↓1 - u↓1·v↓n))}、
と定義する。
これから、Gu(3)=x1/3 + x2/3 + x3/3 - qx、、
また、Gx(3)=(x1 + x2 + x3)/3、であることから、Gu(3)=Gx(3)-Qx、であることが確かめられる。
以下、Gu(n)-Gx(n)+Qx、をn=4~10について、計算すると、すべて、ゼロとなることが分かる」
「そうじゃな。
Gx(3)=(x1 + x2 + x3)/3、であるが、
Gx(4)=((x1^2·(y2 - y4) - x1·(x2·(y1 - y2) + x4·(y4 - y1)) + x2^2·(y3 -
y1) + x2·x3·(y3 - y2) + x3^2·(y4 - y2) + x3·x4·(y4 - y3) + x4^2·(y1 - y3))/(3·(x1·(y2
- y4) + x2·(y3 - y1) + x3·(y4 - y2) + x4·(y1 - y3))))、となり、4角形以上では、3角形と異なり、重心の表式は、複雑になることに注意するようにな。
では、αが必ずしもゼロでない一般の場合じゃ。
(2)αが必ずしもゼロでない一般の場合
u↓k ≔ (x↓k - qx)·COS(α) + (y↓k - qy)·SIN(α)、
v↓k ≔ -(x↓k - qx)·SIN(α) + (y↓k - qy)·Cos(α)、
として、k=1~10まで計算を実行する。
また、Gv(n) ≔ 1/6S(n)(∑((v↓j + v↓(j + 1))·(u↓j·v↓(j + 1) - u↓(j + 1)·v↓j),
j, 1, n - 1) + (v↓n + v↓1)·(u↓n·v↓1 - u↓1·v↓n))、と定義する。
[Gu(3),Gv(3),0]T’=[- (3·qx - x1 - x2 - x3)/3, - (3·qy - y1 - y2 - y3)/3,
0]、(T'は、Tの転置行列)。
すなわち、[Gu(3),Gv(3),0]T’ =[Gx(3),Gy(3),0]-[Qx,Qy,0]、であることが確かめられた。
そして、[Gu(n),Gv(n),0]T’ -[Gx(n),Gy(n),0]+[Qx,Qy,0]をn=4~10まで計算しても、[0,0,0]を返すことが分かる。
ま、この節で取り上げたuv平面がxy平面と同じ平面にある場合は、そもそも、xyz座標系で重心を計算できるんじゃが、(4)節のロジックを確認する意味で、xyz座標系からの座標値をuvw座標系に変換して計算し、再度、xyz座標系に変換し直して確認したというわけじゃ。
さて、次の節では、一般の3次元の場合に備えて回転行列の取り方を考えよう」
目次へ戻る
(6)回転行列(3次元空間)
「(4)節と同様に考えてみよう」
 「まずは、図を用意してと。
「まずは、図を用意してと。
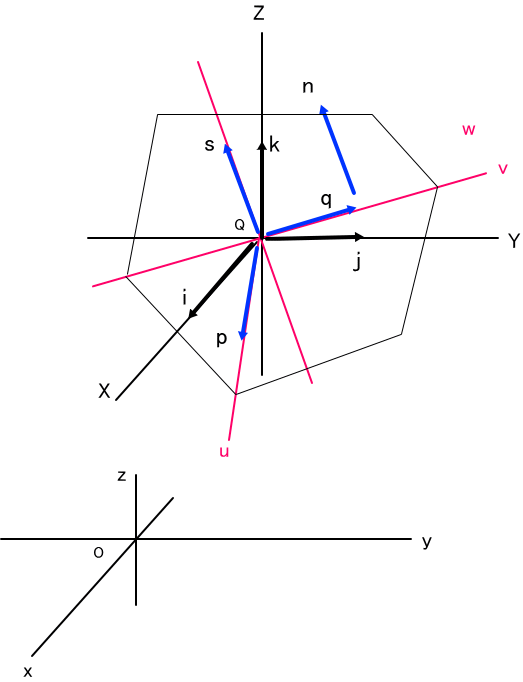
(4)節にならって、θ(u:x)などで、u軸とx軸などとの交角を表すと、
i=p cosθ(u:x)+q cosθ(v:x)+s cosθ(w:x)、
j=p cosθ(u:y)+q cosθ(v:y)+s cosθ(w:y)、
k=p cosθ(u:z)+q cosθ(v:z)+s cosθ(w:z)、
である。
従って、
[u,v,w]=[x,y,z][[cosθ(u:x),cosθ(v;x),cosθ(w;x)],
[cosθ(u;y),cosθ(v:y),cosθ(w;y)],
[cosθ(u;z),cosθ(v;z),cosθ(w:z)]、
Tは、3行3列の行列で、その要素数は、9個なんだけど、
i,j,kの大きさがすべて1で、相互の直交条件が3つあるため、9-(3+3)=3個が独立な成分となるわけね。
で、もう少し、具体的には、多角形の乗っている面の法線ベクトルを n で表すと、
第39回に載っているんだけど、
n=[nx,ny,nz]とxyz成分で書いた場合に、
平面の方程式をαx+βy+γz+δ=0としたとき、
nx = ±α/√(α2 + β2 + γ2) 、
ny = ±β/√(α2 + β2 + γ2)、
nz=±γ/√(α2 + β2 + γ2)、 の関係がある。(複号同順)
また、α等の4つのパラメーターの内、3つが独立なんだけど、
∂/∂αΣ(αxi+βyi+γzi+δ)2=0、から、Σxi(αxi+βyi+γzi+δ)=0、
、∂/∂βΣ(αxi+βyi+γzi+δ)2=0、から、Σyi(αxi+βyi+γzi+δ)=0、
、∂/∂γΣ(αxi+βyi+γzi+δ)2=0、から、Σzi(αxi+βyi+γzi+δ)=0、
、∂/∂δΣ(αxi+βyi+γzi+δ)2=0、から、Σ(αxi+βyi+γzi+δ)=0、
から決定できるということよ」
「ともちゃんが書いてくれた最後の4つの式は、いわゆる「観測方程式」と言われるものじゃ。
つまり、平面は、数学的には、頂点が3つあれば決まるのじゃが、実務的には、頂点の座標値には、誤差がある可能性を考えなくてはならない。
このため、頂点の総数を生かして、α等の計算値に含まれる誤差を減少させようということじゃ。
しかし、今回は、面積ベクトルが得られるため、それからnを決めることができる。
すなわち、n=[nx,ny,nz]、S=面積の大きさとして、
nx=(1/2S)Σ( y(i) * z(i + 1) - z(i) * y(i + 1))、
ny=(1/2S)Σ(z(i) * x(i + 1) - x(i) * z(i + 1))、
nz =(1/2S)Σ( x(i) * y(i + 1) - y(i) * x(i + 1))、
これから、、α、β、γ、δは、α=nx、β=ny、γ=nz、δ=-Σ(αx(i)+βy(i)+γz(i))/頂点総数、と計算する。
残差の2乗和として、Σ(αx(i)+βy(i)+γz(i)+δ)^2は、すべての頂点が同一平面上にあれば、ゼロであるが、誤差があれば、正の値となる。
これで、w軸の方向は、s=nと決めることができて、回転行列の9つの要素の内、3つは、決まったのじゃが、u軸、v軸の方向を決めないと残りが決まらない。
それには、まず、uvw座標系の原点となる Qは、P1とするのが簡単だ。すなわち、OQ=r1=[x(1),y(1),z(1)]、
次にu軸じゃが、測定誤差を減ずるため、p∝(1/頂点総数)(Σri)-r1とする。
すなわち、
p∝[(1/頂点総数)Σx(i)-x(1),(1/頂点総数)Σy(i)-y(1),(1/頂点総数)Σz(i)-z(1)]
最後にv軸じゃが、w軸からu軸に右ねじを回したときの進む方向、すなわち、q=n×p、とすればよい。
これで、
cosθ(u:x)=p・i、cosθ(v:x)=q・i、cosθ(w:x)=n・i=nx、
cosθ(u:y)=p・j、cosθ(v:y)=q・j、cosθ(w:y)=n・j=ny、
cosθ(u:z)=p・k、cosθ(v:z)=q・k、cosθ(w:z)=n・k=nz、
と、回転行列 Tの要素がすべて決定できたことになる」
「じゃ、具体的な例で確認してみるよ。
次のような頂点 P1~P4を持つ4角形を考える。
P1 [5,0,0]
P2 [0,7,0]
P3 [0,0,8]
P4 [1,2,144/35]
これらから、面積ベクトルは、S=[20, 100/7, 25/2] と求められ、面積の大きさ Sは、ABS(S)=5√5961/14、と求めらる。
また、α =20/S= 56/√5961、β = 40/√5961、γ = 35/√5961、
δ=-Σ(αx(i)+βy(i)+γz(i))/頂点総数=-280/√5961、
ちなみに、残差の2乗和は、ゼロとなる。
次に、uvw座標系の座標原点 Qとして、P1をとると、OQ=[5,0,0]、である。
一方、回転行列を求めるためのuvw座標系の単位ベクトルは、
s=n=[nx,ny,nz]=(1/√5961)[56,40,35]、
u軸をΣ(r(i))/頂点総数-r(1)方向にとると、p∝[(1/4)Σx(i)-x(1),(1/4)Σy(i)-y(1),(1/4)Σz(i)-z(1)]から、
p=[-490/√519101, 315/√519101, 424/√519101]、
v軸の単位ベクトル q=n×p=[5935/√3094361061, -40894/√3094361061, 37240/√3094361061]、
従って、回転行列 Tの要素は、
cosθ(u:x)=p・i=-490/√519101、
cosθ(v:x)=q・i=5935/√3094361061、
cosθ(w:x)=n・i=56/√5961、
cosθ(u:y)=p・j=315/√519101、
cosθ(v:y)=q・j=- 40894/√3094361061、
cosθ(w:y)=n・j=40/√5961、
cosθ(u:z)=p・k=424/√519101、
cosθ(v:z)=q・k=37240/√3094361061、
cosθ(w:z)=n・k=35/√5961、
Tは、DERIVEの表示では、下図のようになる。

当然ながら、T*T'は、単位行列となるわ。(確かめて~ ♪)
これで、ようやく、重心を求めるための準備が整ったのね。
[u,v,w]=([x,y,z]-OQ)*T、により、P1~P4までの、uvw座標系の座標値を求めると、
P1 [0, 0, 0]、
P2 [4655/√519101, -53/√3094361061/519101, 0]、
P3 [5842√519101/519101, 45·√3094361061/519101, 0]、
P4 [151706·√519101/18168535, 8·√3094361061/519101, 0]、
となるので、これらから、重心 Gのuvw座標系の値[Gu,Gv,Gw]を求めることができる。
それは、
Gu=(1/6S)Σ((u(i) + u(i+1))(u(i)v(i+1) - u(i+1)v(i))、
Gv=(1/6S)Σ(v(i)+v(i+1))(u(i)v(i+1)-u(i+1)v(i))、
から、
Gu=1859413·√519101/272528025、
Gv=-54·√3094361061/2595505、
Gw=0、となる。
これらから、Gのxyz座標系での座標値 [Gx,Gy,Gz]は、
[x,y,z]=[u,v,w]*T ’+OQ、より、
[Gx,Gy,Gz]=[23/15,3,1112/525]、と求められたとさ。
あー、しんど」
「では、正解を計算してみよう。
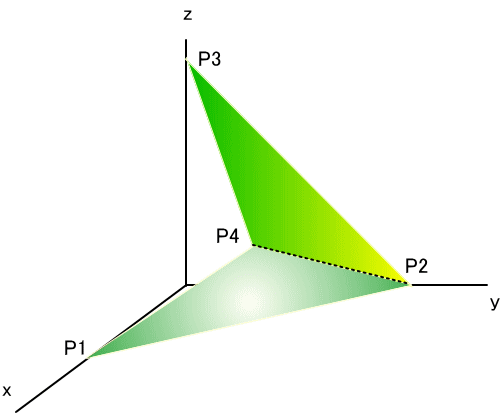
この4角形は、P1-P2-P3-P4 と、上の図のような形をしている。
P1-P2-P4の小三角形の面積は、9√5961/35、重心は、[2,3,48/35]
P2-P3-P4の小三角形の面積は、√5961/10、重心は、[1/3,3,424/105]
2つの小三角形の面積の計は、5√5961/14、面積の重み付き重心は、[23/15, 3, 1112/525]、と求められる」
「合っているわね!
その小三角形の重心は、どうやって求めたの?」
「これは、(1/3)(3つの頂点の座標値の和)としたのじゃ。
この式は、4角形以上では、一般には、成立しないのだが、3角形については、成立するのでな。
ただ、機械的に、P1-P2-P3とP3-P4-P1としたのでは、正しくない結果が得られるので注意が必要じゃ。
なので、自動的に計算するためには、座標変換をして計算した方が、簡単じゃろう。
次節では、多角錘の重心について、考えてみよう」
※青字個所は、2015/10/10に修正しました。(後述(8)節をご参照ください)
目次へ戻る
(7)多角錘の重心
「下図のような、多角錘の重心を考える。
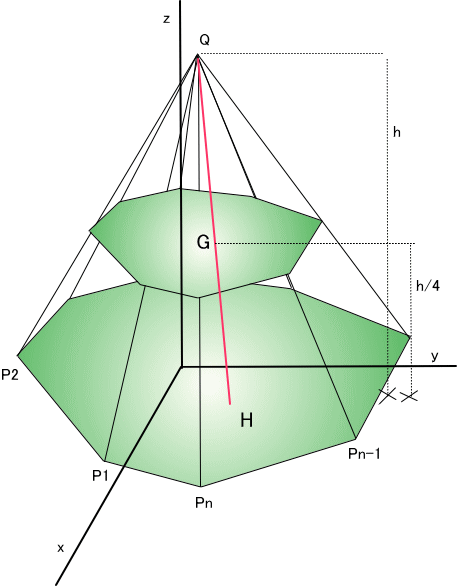
多角錘の底面を外から見て、底面の頂点を反時計回りに、P1~Pnと決める。
また、多角錘の頂点をQ、底面の多角形の重心をHとする。底面にxy平面を置くとき、Hは、[Hx,Hy]であるとする。
このとき、多角錘の重心Gを、[Gx,Gy,Gz]とし、
Gx=Hx、Gy=Hy、であるが、 hは、多角錘の高さとするとき、
Gz=h×1/4、であることを証明してご覧」
 「そうねぇ。
「そうねぇ。
底面の面積をSとすると、Hから高さuの位置にある底面に平行な図形の面積は、S×(1-u/h)^2である。
HG=∫u×S×(1-u/h)^2 du/多角錘の体積、
多角錘の体積 V=(1/3)S×h、
よって、HG=(Sh^2)/12×(3/Sh)=h/4となる」
「ちょっと、注釈を。
底面からの高さuの位置の底面に平行な相似多角形の面積は、S×(1-u/h)^2、というところじゃ。
多角錘の頂点Qから底面を見たときの立体角をωとすると、立体角の定義から、ω=S/h^2 、である。
このとき、底面から高さ uの位置は、頂点からは、h-uの位置にあるので、その位置の相似多角形の面積=ω×(h-u)^2=S×(1-u/h)^2、ということじゃ。
第74回で「カバリエリの原理」をやったのじゃが、それと混同してはいけない。
今回は、多面体の重心を求めようということで、進めてきたんじゃが、だいぶ、紙数も時間もかかってしまった。
もう少しというところではあるが、この続きは、次回に回すことにしよう。
いや、ともちゃんもお疲れさんじゃった」
※取り消し個所に過誤ありましたので、2015/10/13に削除しました。
※多角錘の図を差し替えました。2015/10/15
目次へ戻る
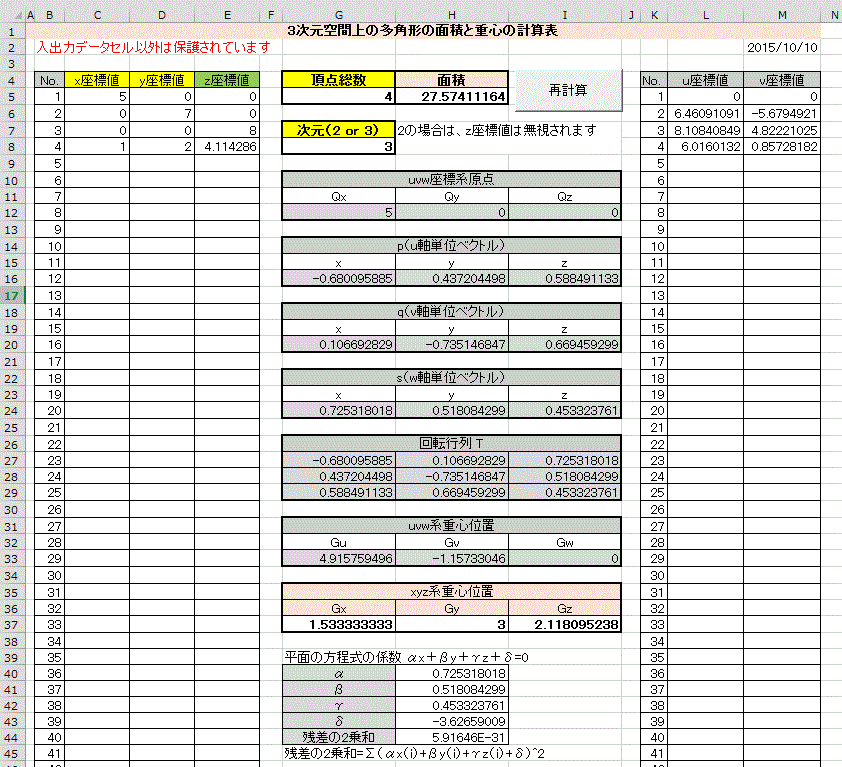
(8)多角形の面積と重心を求めるExcelブック (2015/10/10 追記)
(6)節では、当初想定したα等を座標値から計算で求めることのではなく、面積ベクトルの方向をw軸の単位ベクトルの方向とするように修正しました。(修正部分は、青字)
これは、α等を座標値から計算で求める場合、多角形の乗る平面が、特別な場合、すなわち、xy平面に平行、yz平面に平行、xz平面に平行などの際に α、β、γの1つまたは2つがゼロとなることがあり、その場合を分けて考える必要が出てきます。
また、平面が原点を通る場合は、δをゼロとすることが必要となり、この場合も、分けて考えることになります。
これらは、いずれも、面倒でプログラムが複雑になることから、バグも入りやすくなります。
更に、多角形の頂点の番号の振り方により、正しい重心位置が計算できない場合も発生。
そこで、本節の冒頭のように、面積ベクトルから、w軸を求め、α等は、逆に、それから、計算するように変更しました。
この方法の検証のため、3次元空間上の多角形の面積と重心を計算するExcelブックを作成し、下記にアップしました。
TakakukeiVer2.xlsm です。
これは、10/7にアップした「TakakukeiVer1.xlsm」を修正したものです。
もし、TakakukeiVer1.xlsmをダウンロードした方ば、お手数ですが、削除していただき、あらためて、上記ファイルをダウンロードしてください。
ブックは、Excel 2013で作成し、計算には、Excel VBAを使用しています。(Excel 2007、2010でも動作します)
ダウンロードしたものは、適当な場所に保存してから開いてください。
開く際、セキュリティの警告が表示された場合は、適宜、「コンテンツの有効化」等(Windows あるいはOfficeのバージョンによって警告等の内容と動作は変わります)を選択してください。
なお、すでに4点のデータが入力・計算されています。これらのデータは、(6)節のものです。
利用する頂点の座標値を入力後、「再計算」ボタンをクリックしてください。
次元は、2又は3です。(次元が2の場合は、z座標値は、入力されていても無視されます)
結果は、面積、xyz系の重心位置、平面の方程式の係数及び残差の2乗和等が表示されます。
計算には、倍精度浮動小数点型の変数を使用していますが、有限桁数なので、残差の2乗和は、(6)節の例では完全なゼロとはなりません。
頂点総数は、100点まで利用できます。
シートは、保護していますので、入出力用のセル以外の編集はできませんが、「シートの保護を解除」することで編集は、可能となります。
なお、動作の保証は、できかねますので、自己責任にて、ご利用ください。(改変は自由です)
目次へ戻る
最終更新日:2015/10/15
一部追記:2017/4/7
目次修正:2021/10/27



 「そうだったわね。
「そうだったわね。







