まぁ、そんなわけで、今回は、わたし、ともちゃんが解説しますね。「 」書きは、省略しますよ。まずは、行列式の定義ね。「えー、定義からなの！」って、思った方もいるでしょ。定義⇒定理⇒例題、という流れって「数学あるある」じゃない！、いやだよね。だけど、やっぱり、定義からいきます。その代わり、面倒な証明は、省いて、納得感の得られる説明を心がけます。厳密な証明が欲しいという方は、適切な教科書、参考書を参照くださいな。1.はじめに
2.行列式の定義と2次、3次の行列式
（1）行列式の定義
（2）互換、置換の対象
（3）互換、置換の行列表現
（4）行(ROW)と列(COLUMN)
（5）2次、3次の行列式
3.行列式の帰納的計算
（1）3次の行列式と余因子
（2）DERIVEのベクトルと行列の関数
（3）行列式の帰納的ユーザー定義関数
4.行列式の歴史
（1）概要
（2）2元連立1次方程式
① 鶴亀算
② 2次行列式の芽生え
（3）3元以上の連立1次方程式
（4）一般の連立1次方程式
5.行列式の基本的性質
（1）転置行列の行列式は不変
（2）行(列)の交換で行列式の符号が反転
（3）二つの行(列)が等しい行列式はゼロ
（4）一つの行(列)の要素を定数倍で行列式も定数倍
（5）複数の行列式の和に分解
（6）行(列)×定数を他の行(列)に加えても値は不変
（7）行(列)の1つ以外の要素が0で次数が下がる
今回は、平均日数公式をもう少し、展開していくため、『行列式（1）』と題して、行列式の基本的な性質をおさらいします。次回の『行列式（2）』では、もう少し進んだ内容を取り上げる予定です。その後、これらの行列式の性質を使い、第96回『マルコフ過程（8）（非対称型道中双六：基本対称式の準2次形式）』の4.『Ψのuk分解』で触れた、平均日数公式のuk分解を具体的に書き表していきたいと考えています。
今回の『行列式（1）』では、Vandermonde（ファンデルモンド、あるいは、ヴァンデルモンド）の行列式も登場します。『行列式』は、だいぶ、昔に、ともちゃんに宿題にしていましたので、ここからは、ともちゃんにお任せすることにしましょう。では、ともちゃん、どうぞ！
目次へ戻る
まぁ、そんなわけで、今回は、わたし、ともちゃんが解説しますね。「 」書きは、省略しますよ。まずは、行列式の定義ね。「えー、定義からなの！」って、思った方もいるでしょ。定義⇒定理⇒例題、という流れって「数学あるある」じゃない！、いやだよね。だけど、やっぱり、定義からいきます。その代わり、面倒な証明は、省いて、納得感の得られる説明を心がけます。厳密な証明が欲しいという方は、適切な教科書、参考書を参照くださいな。
さてと、行列式の定義って、分かりにくくないですか？ たとえば、『行列と行列式』（古屋茂 著：培風館：1970年増補第2刷）では、n次の正方行列Aの行列式、|A|は、概ね、下の青字のように定義されているわ。ここで、a11などは、行列Aの要素よ。Aが3次行列では、下図のように書き表されるわね。
※ 下添え字は、本来、p1、a11などと書けばいいんだけどHPでは、書きづらいので、p1、a11、などと書きますね。
|A|=Σε(p1,p2,・・pn)a1p1×a2p2×・・×anpn、
ここで、Σは、(1,2,・・n)という数の並び（順列）について、2つの要素を入れ替える操作（互換）を複数回行ってできる順列を(p1,p2,・・・pn)としたとき、すべての異なる順列に関する和をとる。また、εは、その順列が『偶順列』であれば、+1を、『奇順列』のときは、－1をとる関数とする。
なお、『偶順列』とは、、偶数回（ゼロ回も含む）の互換を行うことで得られる順列、『奇順列』とは、奇数回の互換を行うと得られる順列である。全体の個数は、n個のすべての並びの個数、すなわち、n！個であり、その半数が偶順列、残りが奇順列となる。
この定義に従うと、3次行列Aの行列式は、
となるのね。要素、aの下添え字の2番目の数に注目していただくと、123、231、312、の前半3項が偶順列に基づく項、321、213、132となる後半3項が奇順列に基づく項となることがわかるでしょ。
ここで、簡単に「なるほどね」なんて、言えるのは、「紫さん、あんたくらいよ」。ごめん。勝手に「清少納言スイッチ」が入っちゃったみたい。もしかすると、古い本だからじゃないか、とお疑いの方もいらっしゃるかも知れないけど、新しい本でも、行列式の定義は、特に変わらないの。
もちろん、行列式の定義は、あとで書くような帰納的な定義を取ることもできる。数値計算上は、帰納的な定義の方が分かりやすい。でも、行列式のいろんな性質（定理）を証明する上では、前述の定義に比べて、難しくなってしまうみたい。
目次へ戻る
0回を含めて複数回の「互換」を適用することを一般に「置換」と呼ぶ。例えば、(1,2,3)から(2,3,1)を得る置換は、すぐ後に述べるように、互換を2回行っている。そこで、互換に注目！
さて、「互換」は、何を対象としていると思いますか？ (1,2,3・・,n)の中の数自体？、それとも、( )内の最初の位置を1番目としたときの順番なのか？
まず、数自体と考えた時は、(1,2,3)から(2,3,1)を作る場合、1⇔2を交換すると、(2,1,3)となる。これを簡単に、(1,2,3)(1,2)⇒(2,1,3)、と書くわよ。続けて、(2,1,3)で1⇔3を交換すると、(2,1,3)(1,3)⇒(2,3,1)となる。ちなみに、この2つの交換操作の順を入れ替えると、(1,2,3)(1,3)⇒(3,2,1)、(3,2,1)(1,2)⇒(3,1,2)、となって、先ほどの(2,3,1)とは異なる並びとなるのがわかる。
次に互換の対象をかっこ内の順番とした際、上と同じ(2,3,1)になるためには、まず、( )内の1番目と2番目を入れ替えて、(1,2,3)(1,2)⇒(2,1,3)、続けて、( )内の2番目と3番目を入れ替えて、(2,1,3)(2,3)⇒(2,3,1)、である。前述の考え方との違いを赤い( )で表している。ちなみにこの2つの操作の順を入れ替えると、(1,2,3)(2,3)⇒(1,3,2)、(1,3,2)(1,2)⇒(3,1,2)、となって、先ほどの(2,3,1)とは異なる並びとなる。
前掲の古屋先生のご本は、数自体の入れ替えと読める。そもそも、「順列」とは、n個の相異なるものを勝手な順に一列に並べたものなので、相異なるものを、1、2、・・・n、の自然数と対応させて簡便に表しているのね。だから、イメージとしては、トランプのカードを並べるようなもの。手品師でもなければ、並べるとき、カードの元の位置を考えないでしょ。目の前のカードの印や数字に着目して、並べるでしょ。だから、この考え方は、自然に感じられると思うわ。
一方、コンピューターのプログラムでは、順列が変数や配列に入っているでしょう。そうなると、結果的に配列の中身を入れ替える目的ではあるけれど、配列の何番目と何番目の要素を入れ替えたらよいかと考える、つまり、配列の添え字を互換の対象と考えるので、後者の考え方となる。わたしは、こっちの考え方が分かりやすいわ。あー、もちろん、2つは、異なる考え方だけど最終的に得られるすべての順列（の集合）は、同じになるわよ。
目次へ戻る
（2）の後の考えをベクトルと行列を使って具体的に書く。最初の順列を[1,2,3]と横ベクトルとして、ベクトルの1番目と2番目の要素を入れ替える互換、(1,2)は、[[0,1,0],[1,0,0],[0,0,1]]という3次行列で表すと、
[1,2,3]×[[0,1,0],[1,0,0],[0,0,1]]=[2,1,3]となる。
同様にベクトルの2番目と3番目の要素を入れ替える互換、(2,3)は、[[1,0,0],[0,0,1],[0,1,0]]とすれば、
[2,1,3]×[[1,0,0],[0,0,1],[0,1,0]]=[2,3,1]が得られる。綺麗に書けば、下図のようになるでしょう。
※ このような行列は、順列の置換が形作る置換群の行列表現と呼ばれる。
もう一つの互換 (1,3)が[[0,0,1],[0,1,0],[1,0,0]]なのね。この3つの互換を表す行列とそれらの2つの積（の一部）で、下図のように、6通りすべての順列が得られるのよ。
上図の3つの互換を表す行列、α、β、γは、奇順列を導く。
※ |α|=|β|=|γ|=－1、に注意してくださいな。
また、赤い曲線は、|A|の負符号となる3つの項の積に対応する。（後述）
α、β、γの2つの積の一部から、偶順列が導かれる。
※ |αγ|=|βγ|=|E|=1、に注意してね。
『行列と行列式』（P165）では、このような行列を『順列行列』と呼んでいる。
順列行列は、直交行列である。（α×α'=E：単位行列、すなわち、αなどの逆行列は、その転置行列である）
順列行列の行列式は、偶順列の時は、+1、奇順列の時は、－1である。
青い曲線は、|A|の正符号の項の積に対応する。
なお、上に現れない、α×β（=β×γ）、β×α（=α×γ）、γ×α（=β×γ）、γ×β（=α×γ）、となって、既出の6個の置換であることが確かめられる。
大事なのは、行列の1の位置に注目すること。各行、各列の和は、常に1なので、すべての行、列に1は、1回必ずあり、かつ、1回しか現れないことが分かるでしょ。この性質から置換を表す行列は、n!個なのね。（1行目では、1をn通りに置く列があり、2行目では、n－1通りの列があり、以下同様となるから、全部で異なる行列は、n!個となるため）
なお、3次の例では、互換が3つあったけど、一般のn次行列では、nC2=n(n－1)/2、個あるのね。例えば、n=4では、互換は、6個あるので、すべての置換、4!=24の残り、24－6=18個は、互換の積から作り出せる。（6C2=15，6P2=30、から、15<18<30、なので、3次行列と異なり、互換の2つの組だけでは足りず、互換の2つの積の順序を入れ替えた一部も含まれるか、または、3つの互換の積（の一部）も含まれるのではないかと予想できる。次回、確かめるわよ）
目次へ戻る
行列の行と列って、どっちがどっちだっか、混乱することがあるでしょ。ちなみに、英語の数学用語では、ROW（ロー）が「行」を、COLUMN（カラム）が「列」を表します。ジーニアス英和辞典では、それぞれに数学での用例が正しく載っていました。
ただし、数学以外では、ROW、COLUMNのいずれも「列」と解釈されることがありますよ。これは、日本語でも「列」と書いたり、言ったりしたとき、数学用語の意味で使うとは、限らないのと同じね。たとえば、「縦（または横）一列に並んでください」とは言うけど「縦（または横）一行に並んでください」とは、言わないでしょ。それで、よけいに「行列」のどっちが行で、どちらが列だったかが分からなくなり易い。
ちなみに、表計算のExcelでは、セル内に、=ROW(C5)は、5を返し、=COLUMN(C5)は、3（=C列）を返すことからも、ROWが「行」を、COLUMN（カラム）が「列」に対応するすることを確かめられるわよ。
目次へ戻る
この節の終わりに、2次と3次の具体的な行列式を取り上げますね。
まずは、2次の場合、|A|=a11×a22－a12×a21、これは、たすき掛け計算法（関・サラスの方法）として知られている。付け足すと、1次の行列式は、a11、自身と考えれば、いいわね。
上の図で、青い線は、プラス、赤い線は、マイナスの項を表す。
※ 関孝和は、『江戸前期の和算家。通称新助。生地不詳。傍書法（筆算式の記号法）を考案し、開方式（方程式論）・伏題(ふくだい)（未知数の消去法）・角術（正多角形）・円周率などを研究した。著「大成算経」「括要算法」「発微算法」など。（1640頃～1708）』（広辞苑第7版）
3次の場合は、すでに挙げているけど再掲しますね。
たすき掛け計算は、下図のように覚えていると思うわ。
青い曲線は、正符号、赤い曲線は、負符号に対応します。
なお、サラスの方法では、同じことを次のように表すんだって。ダミーとして、4列目と5列目を作り、6本の直線で下図のように結びます。青い線は、正符号、赤い線は、負符号に対応。
※ サラスとは、『ピエール・フレデリック・サラス（Pierre Frédéric Sarrus、1798年3月10日 - 1861年11月20日）。フランスの数学者』（ウィキペディア）のこと。『サラスの方法』は、彼が発案した3次行列式の記憶方法のこと。
目次へ戻る
このように、2次、3次では、簡単に計算できる行列式の計算なんだけど、4次、5次と次数が増加すると、定義に従って計算すると手間がかるのね。n次行列式の場合、定義からは、n!個の項目の和を取る必要がある。1つずつの項は、n個の要素の積からなっているため、全体の積算回数は、n!×n個、程度となる。
もちろん、これは、すべての要素が数の場合ね。要素が数でない場合、たとえば、互いに異なる変数とかだと積の計算量が減る可能性は、あるでしょう。（DERIVEのような数式処理では、実際の数でない変数の積は、複数の変数を単に並べるだけなので）
とはいえ、4次で24個、5次で120個、・・の項を間違えずに計算するのは、大変。ツルカメツルカメ。そこで、ビジュアルに分かりやすい「たすき掛け計算」に変わる方法が求められる訳ね。その一つが帰納的計算法（行または列で行列式を展開）。これは、3次の行列式を注意深く見直すと、どなたでも容易に推察できると思うの。
3次行列、Aの行列式は、DERIVEでは、DET(A)で、計算できるけど、1行目の要素、a11、a12、a13でくくると、
|A|=a11·(a22·a33 － a23·a32) + a12·(a23·a31 － a21·a33) + a13·(a21·a32 － a22·a31)、と表される。
ここで、それぞれのかっこ内が下図のように2次の行列式で表されることに気がつけば、
と書き改めることができるでしょう。
なお、2項目だけ負符号を付けている理由は、以下で説明しますね。
まず、第1項目、下の図の⇔の右側が元の3次行列式だけど、1行目（水平のオレンジ色の直線）と1列目（垂直のオレンジ色の直線）を除いてみると、青い長方形で囲まれた部分を要素に持つ左側の2次の行列式なのね。これがかっこ内の式と一致する。
以下第2項目は、1行目（水平のオレンジ色の直線）と2列目（垂直のオレンジ色の直線）を除いてみると、青い長方形で囲まれた部分を要素に持つ左側の2次の行列式となる。かっこ内の(a23·a31
－ a21·a33)と合わせるために負号を付けた意味が出てくる。
3項目も同様に、1行目（水平のオレンジ色の直線）と3列目（垂直のオレンジ色の直線）を除いてみると、青い長方形で囲まれた部分を要素に持つ左側の2次の行列式。
さて、いちいち、「1行目と3列目を除いた・・」などと説明するのは、面倒なので、新しい用語が登場するのね。用語は、便利なんだけど、増えていくと、どれがなにやら、となり勝ちなので、注意してね。まずは、『小行列式』、これは、元の行列から、j行目とk列目を除いた行列の行列式のこと。
※ 前述の「行列と行列式」では、小行列式を、
、で表しているけど、Aの(j,k)要素と紛らわしく、かつ、Webでは、書きづらいので、この記法は、使いません。
この小行列式に(－1)^(j+k)という符号を付けたものが『余因子』です。3次行列の1行目での展開では、1行目とk=1～3列目までを除いた小行列式に符号を付けた余因子が使われている。
『余因子』を使うと、3次行列式は、
|A|=Σ(k=1～3)（a1k×余因子(1行目，k列目)）、
のように1行目の要素と余因子（2次行列式を計算したスカラー量）で展開できることが分かります。
目次へ戻る
ところで、DERIVEで使うベクトルや行列に関する基本的な演算や関数は、すでに紹介しているわね。たとえば、ベクトルの内積や外積、行列の加減乗算、転置、ベクトルと行列の乗算、逆行列、行列式など。
一方、前節で出てきた『余因子』などは、DERIVEのファイルメニューから読み込みで、mathファイルから、「LinearAlgebra.mth」を取り込むと利用できます。いくつか紹介しますね。
DELETE(M，i)は、行列Mから、i行目を削除した行列を表す。
MINOR(行列，i行，j列)は、行列Mから、i行、j列を取り除いた行列、
ユーティリティでは、MINOR(M，i，j):=（DELETE(DELETE(M，i)’)’、と定義されている。
ここで、DELETE(M，i)は、前述のように行列Mからi行目を削除した行列を表す。また、アポストロフィは、行列の転置を表す。
※ 転置を2回使っている理由は、DELETE関数は、行の削除だけに対応しているため、行列からi行とj列を取り除くためには、まず、i行の削除を行い、次にj列の削除をするため、一度、行列を転置し、j行として、その削除を行い、再度、転置して戻す必要があったからね。
COFACTOR(M, i, j)は、行列Mをi行、j列で展開する場合の余因子。（スカラー量）
ユーティリティでは、余因子、COFACTOR(M, i, j):=COS(·(i + j))·DET(MINOR(M, i, j))、と定義されていることが、ユーティリティファイルを読むと分かるわよ。
なお、COS(·(i + j))は、(－1)^(i+j)と等価で、DERIVEでは、内部的にこのように計算する習慣がある。関数名のCOFACTORは、英語では、余因子をcofactorと呼ぶことによります。DETは、既出の行列式を求める関数。
余因子関数を使うと、3次行列式を1行目での展開した式は、
Σ(ELEMENT(A，1，k)*COFACTOR(A，1，k),k,1,3)、と書くことができます。
ここで、ELEMENT(A，1，k)は、行列Aの(1,k)要素を取り出す関数。
この計算結果は、下図の通りで、DET(A)と一致するのを確かめられる。
ただし、上の方法では、3次行列式を2次行列式で展開してるけど、2次行列式は、COFACTOR関数の働きによりスカラー量に一気に計算されてしまうため、次節で説明する「帰納的な計算式」にはなっていないことに注意してくださいね。
目次へ戻る
前節の最後の式を参考にして、DERIVEの行列式、DET(A)と同等な働きをする「帰納的ユーザー定義関数」を作ってみましょう。肝は、Cofactor関数を使わないこと。これを使っちゃうと（引数で指定した行列の「行列式」がスカラー量として）計算されてしまいます、この点に注意して、関数名をFdet_user(A_)として、以下のように定義します。
Fdet_user(A_) ≔
PROG(
n_ ≔ DIMENSION(A_),
IF(n_ = 1,
ELEMENT(A_, 1, 1),
∑(ELEMENT(A_, 1, k_)·(－1)^(1 + k_)·Fdet_user(MINOR(A_, 1, k_)), k_,
1, n_)))
※ 3次行列式の展開におけるCOFACTOR関数をFdet_user(MINOR(A_,1,k_))×(－1)^(1+k_)で置き換えています。
※ DIMENSION関数は、ベクトルや行列の次元を与えるDERIVEの関数です。
※ 関数内部でのみ利用するローカル変数名に、A_やn_のようにアンダーバーを付けて区別するのがマイルールです。
（DERIVEでは、ローカル変数とグローバル変数の区別がないので、誤って、外部でローカル変数の値を変えないための用心）
さて、ユーザー定義関数を使ってみると、3次と4次行列の行列式の計算結果は、下図の通り。
3次の場合は、
4次の場合は、
(a11·(a22·(a33·a44 － a34·a43) + a23·(a34·a42 － a32·a44) + a24·(a32·a43 － a33·a42)) － a12·(a21·(a33·a44 － a34·a43) + a23·(a34·a41 － a31·a44) + a24·(a31·a43 － a33·a41)) + a13·(a21·(a32·a44 － a34·a42) + a22·(a34·a41 － a31·a44) + a24·(a31·a42 － a32·a41)) － a14·(a21·(a32·a43 － a33·a42) + a22·(a33·a41 － a31·a43) + a23·(a31·a42 － a32·a41)))
いずれも、DET関数を使った計算結果と差し引きして一致することを確かめています。なお、上のような帰納的計算は、行列式の計算法としては、2.（1）の定義から計算するのと比較しても、能率的ではないけど、分かりやすい面は、あるわね。これを行列式の帰納的定義とすることもできます。
目次へ戻る
「行列式」は、歴史的には、連立一次方程式を解くことがきっかけで考え出されたと思うわ。でも、その歴史を簡単に振り返った本が手元になかったので、いくつかのサイトを参照した結果の一部を下に引用させていただきました。
『FNの高校物理』、http://fnorio.com/editorial_policies.htm、の『行列と行列式』を参照すると、以下の青字の個所のように、行列と行列式の歴史が簡潔に書かれていた。なお、そこでは、参考文献として、藤原松三郎著「岩波全書 行列及び行列式（改訂版）」岩波書店（1961年刊）が挙げられています。
『行列式の理論はもともと連立1次方程式を解く手法として始まった。その紀元は古く9世紀頃のインドの数学・天文学者ブラーマゲプタの書や、その後の関孝和「解伏題之法（1683年）こちらも参照」やライプニッツの書などにもその萌芽が見られる。そして行列式を一般的に定義し、その性質を論じ始めたのはクラーメル（Cramer）です。行列式を表す、deternimant、という語句はガウスが二次形式の理論において、今日「判別式」(detrminant）といっているものにつけた名称ですが、コーシーが行列式をその様に呼ぶことにして以来今日ではその名称が定着している。
歴史的には「行列式」の理論がはるかに先行しており、「行列」の理論はケーリー（Cayley）の1858年の論文から始まる。行列を表す「matrix」という名称はシルヴェスタ（Sylvester）が付けたもので、彼は invariant、covariant、contravariant、eliminant、なども名付けた。日本語で「行列」と名付けたのは、高木貞治あたりに始まるようです。』とありました。
なお、クラメールは、『ガブリエル・クラメール (仏語: Gabriel Cramer、1704年7月31日 - 1752年1月4日) は、スイスの数学者である。クラメールはジュネーヴで生まれ、早くから数学の才能を見せ、18歳で博士の学位を授与され20歳で数学の副主任となった。（中略）クラメールの公式はその論文（1750年）の中で紹介されているが、コリン・マクローリンは同様の公式を1748年に公表している。』（ウィキペディア）
ここで、行列について、ひと言、付け加えると、20世紀初めの量子力学が建設されている時、『行列力学』（1925年）を発見した『ハイゼンベルク』が『行列』を知らなかったというエピソードがあります。ハイゼンベルクからエネルギーの表のアイデアを聞いたゲッチンゲン大学でハイゼンベルクを指導していた『ボルン』、『ヨルダン』らは、それが数学で使われていた「行列」であることを見抜いた。20世紀の初めの理工学生にとっては、現在、『線形代数』として大学教養課程で習う内容になじみがなかったことがうかがえるエピソードです。
※ 『部分と全体』（ハイゼンベルク著：山崎和夫訳：1974年10月第2刷：みすず書房）で、ハイゼンベルクは、その時のことをこう記述している。『このようなある晩、エネルギーの表、あるいは、今日の言葉でいうと、エネルギー行列、の個々の項を、今日の尺度から言えば、はなはだ、見通しの悪い計算によって定めることができるという所まで到達した』
このハイゼンベルクの記述について、訳者の山崎和夫氏は、注釈の（4）（P114）に『ハイゼンベルクが行列力学を発見したとき、この記述からもよくわかるように、行列を知らなかったことは有名である。彼の師の数理物理学の達人ゾンマーフェルトから、彼は、主として、関数論の方面を学んでおり、複雑な複素積分などは、得意であったが、今日では大学教養課程で学ぶ程度の一次代数、行列は当時まだ物理学者の共有の知識とはなっていなかった。しかし、ゲッチンゲンのボルンやヨルダンは行列を知っており、ハイゼンベルクのこの話を聞いてすぐそれが行列を用いれば簡単に書き表せることを見抜いた（後略）』
目次へ戻る
「鶴亀算」のような2元連立1次方程式は、中国の数学書の影響を受けて、日本では、江戸時代初期あたりから、世間一般に広まっていったと考えられます。具体的には、台東区立桜橋中学校の永井信一氏の『鶴亀算の系譜』と題する雑誌記事から引用させていただくと、
『最も古い例は、中国の『孫子算経』（3世紀頃）であり、雉と兎を例にしている。その後、『算学啓蒙』（朱世傑：1299年）に鶏と兎で、また、『算法統宗』（程大位：1592年）に、やはり、鶏と兎、また、一頭九尾の狐狸と九頭一尾の鵬鳥を例にした類題も掲げられている。
江戸時代の日本では、『因帰算歌』（今村知商：1640年）に、きじとうさぎ、『算法闕疑抄』（礒村吉徳：1661年）に、雉とうさぎ、『鞍迫観音算額』（岩手県：1743年）に雉子と兎、『算法天竄指南録』（坂部広胖：1815年）に至って、ようやく、鶴と亀が登場した。
明治以降は、通称、黒表紙教科書（1905年～1934年）では、登場していない。その後の、緑表紙教科書（1935年～1940年）以降、水色表紙教科書（1941年～1945年）、検定教科書（戦後～現代）で登場するようになった。典型的な問題は、「鶴と亀が合わせて20匹、足の数が52本、それぞれ何匹いるか？」など。』と言うことでした。
そう言えば、おじぃさんも、小学生の時、鶴亀算で頭を悩ましたと言っていたわ。当時、仮定法という解き方を教わったらしいの。上の例では、「問題（条件が2つある）の条件1を満たすように、仮に、鶴を20匹、亀を0匹とすると、足の本数は、2×20+4×0=44、となる。ところが、問題の条件2では、これが52となるべきで、その差、52－44=8は、鶴と亀を20と0と仮定したために不足した足の数である。そこで、鶴と亀の足の数の差が、亀－鶴=4－2=2、なので、不足している、8を両者の差の2で割って得た4を亀の0に加え、また、同数を鶴の数より引く必要がある。すると、鶴は、20－4=16、亀は、0+4=4、となる。念のため、検算すると、鶴+亀=20、2×鶴+4×亀=2×16+4×4=52、となって題意を満たしていることが分かる」というような解き方ね。
おじぃさんがわかんなかった点は、2つね。一つは、なぜ、亀の足4本－鶴の足2本の差の2で、足りない足の数8を割るのか？ 二つ目は、なぜ、鶴を20匹、亀を0匹と仮定したのか？。
一つ目の疑問は、（仮定した鶴と亀の数では）足の合計本数が足りないので、（鶴より足の多い）亀を増やしたいのだけど、増やした亀の数だけ、鶴の数を減らす必要がある、なぜって、そうしないと条件1が満たせないからね。すなわち、亀1匹増やして、鶴を1匹減らすと、頭数は変わらないけど、足の本数は、差し引き、2本増える。この操作により、足りない足の本数、8を埋めるには、8÷2で、4匹の亀を増やすとちょうど良いことが分かる、と説明すれば、よいでしょう。
二つ目の疑問は、条件1を満たすような数の組ならば、何でも良いんだけど、その適当さがガッテンできなかったみたい。これは、当時、中学で習う予定の未知数x、yを使わないと完璧には、説明困難だわね。
余談だけど、『割り算』にも似ているところがある。小学校で、足し算、引き算、かけ算と順調に来ても、割り算でつまずく生徒さんがいるという。割り算では、『試し割り算』という考えが必要なのね。例えば、365÷8=44 余り 3、という計算で、九九を一応言えるようになっていても、36の中に8がいくつあるか、同様に35の中に8がいくつあるかというのは、直ちには、出てこないのよ。これは、コンピューターの基本的な演算でも同様で、計算速度は、加減算<<乗算<除算、の順に大きくなるという。
目次へ戻る
ウィキペディアの行列式の歴史によれば、『『詳解九章算術』（楊輝（中国、1238年?～1298年））は、数字係数の二元連立一次方程式の解をクラメルの公式の形で、行列式的なものを含んだ形で与えている。また1545年にジェロラモ・カルダノは、著書 Ars Magna の中で同じく2×2の場合のクラメルの公式を与えている。この公式は regula
de modo（ラテン語で「様態に関するの規則」の意味）と呼ばれている。彼らは「行列式」を定義したわけではないが、その概念の萌芽を見てとることができる。』
※ 『カルダノ』については、第93回の『マルコフ過程(6)(非対称型道中双六：平均日数と対称式)』の『代数方程式 小史』に触れています。
目次へ戻る
ウィキペディアの行列式の歴史によれば、『関孝和による「括要算法」（1712年）、高階の行列に関する行列式の定義はそれから百年ほどたって日本で和算の関孝和、田中由真、そしてドイツのライプニッツによりほとんど同時にかつ独立に与えられた。（中略）ライプニッツは数多くの線型方程式系を研究していたが、その頃は行列記法がまだなかったので、彼は未知数の係数を、現在のような ai,j のかわりに ij のように添字の対によって表現していた。1678年に彼は3つの未知数に関する3つの方程式に興味を抱き、列に関する行列式の展開式を与えている。同じ年に彼は4次の行列式についても(符号の間違いを別にすれば)正しい式を与えている。ちなみにライプニッツはこの成果を公表しなかったので、50年後に彼とは独立に再発見されるまでこの成果は人々に認識されていなかった
一般的な行列式について、関孝和は、最初の手稿からやや後の『大成算成』（建部賢明、建部賢弘と共著、執筆は1683年（天和3年） － 1710年（宝永7年）頃）で、第一列についての余因子展開を一般の場合について正しく与えている。また、田中由真は『算学紛解』（1690年（元禄3年）ごろ）で 5次までの行列式を、井関知辰は『算法発揮』（1690年（元禄3年）刊）で第一行についての余因子展開を一般の場合で与えている。ちなみに関や田中の著作は写本のみであるが、井関の著作は出版がなされている。』
目次へ戻る
ウィキペディアの行列式の歴史によれば、『1750年にクラメルは（証明抜きで）N 個の変数に関する N個の方程式からなる方程式の解を求める規則を定式化した。この行列式の計算方法は順列の符号に基づく繊細なものだった。ベズー（1764年）やファンデルモント（1771年、ヴァンデルモンドの行列式の計算）などがそれに続き、1772年にはラプラスによって余因子展開の公式が確立された。さらに翌年にはラグランジュによって行列式と体積との関係が発見されている。今日の determinant（決定するもの）に当たる言葉が初めて現れたのはガウスによる1801年の Disquisitiones Arithmeticae である。そこで彼は二次形式の判別式（今日的な意味での行列式の特別な例と見なせる）を用いている。彼はさらに行列式と積の関係についても後少しのところまでいっている。』ということで、19世紀になって、ほぼ、今日の基本的な姿が確立されたことがわかるわ。
現代では、もちろん、コンピューターの発達に伴い、大きな次元の連立1次方程式を解くことができるようになっている。そのため、ガウスなどによる古典的な計算方法より、短時間で計算できるアルゴリズムが工夫されている。これは、行列式、逆行列、固有値などの数値計算でも言える事ね。だけど、それらの歴史やアルゴリズムについては、このページでは、触れる余裕がありません。
目次へ戻る
ここから、ようやく、行列式の基本的な性質に進みますよ。定理と言ってもいいけど、重たく感じると思うので、性質としています。
行と列とを入れ換えても行列式の値は、変わらない。すなわち、正方行列、Aの行列式とその転置行列、A’の行列式は、同じ値となる、ということね。これがどれだけうれしいかというと、こいつが成立すると、行について成立する性質は、そのまま列についても成立することが保証されるからなの。
2次元の行列Aの転置行列、A'の行列式は、下図からもあきらかなように、|A'|の正負の2項の内、正符号のa11×a22は、対角要素であるため、転置を行っても変化せず、また、負符号のa12×a21の項は、転置により、a12⇔a21の交換が行われるも積の順序が変わるだけで値は、等しいため、|A|=|A'|となる。これは、一目でわかるでしょう。
次の3次行列A、その転置行列、A'、についても、|A|=|A'|、であることは、2次行列と同様の方法で証明は、可能ね。だけど、ここでは、別の説明を考えましょう。要素の記法は、以下のようね。
この2つの行列の行列式は、以下の図のようになり、
対応する項同士を矢印で結んで、|A|=|A'|、であることを示したつもりですよ。
さて、一般の場合を証明する手順を3次元の場合で説明するために、定義から、|A|=Σε(p1,p2,p3)a1 p1×a2 p2×a3 p3、
一方、転置行列の行列式は、|A'|=Σε(q1,q2,q3)aq1 1×aq2 2×aq3 3、である。
ここで、(p1,p2,p3)、(q1,q2,q3)に関するΣは、いずれも、(1,2,3)の相異なるすべての順列を動きます。
2.（3）に示した順列行列は、6種類あり、再掲すると、互換からなる奇順列を導く3つがα、β、γ、であり、
その組み合わせで、偶順列を導く3つが、α×γ、β×γ、E（=単位行列）、の3通り。
恒等置換（E）では、|A|、|A'|の対角要素、ε(1,2,3)a1 1×a2 2×a3 3、の項は、まったく変わらないことは、明らか。
互換については、たとえば、αでは、[1,2,3]α=[2,1,3]であるので、
|A|では、ε(2,1,3)a1 2×a2 1×a3 3、の項に対して、
|A'|では、ε(2,1,3)a2 1×a1 2×a3 3、が対応する。よく見ると、a1 2×a2 1の積の順序が異なるだけで、項全体としては、値が同一である。
複数の互換からなる置換では、少し、事情が異なる。たとえば、αγでは、[1,2,3]αγ=[2,3,1]となり、
|A|では、ε(2,3,1)a1 2×a2 3×a3 1、の項に対して、
|A'|の、ε(2,3,1)a2 1×a3 2×a1 3、は、積の順序を入れ替えても同一の値にはならないが、
ε(3,1,2)a3 1×a1 2×a2 3、は、積の順序を交換すれば、赤字個所は、同一の値となる。
なお、[3,1,2]=[1,2,3]γα=[1,2,3]βγ、であり、偶順列なので、εの値も同一である。
この[3,1,2]=[1,2,3]γα、で分かるように、[1,2,3]αγ⇒[2,3,1]の際のαγを逆に並べたものになるところがミソ。
もう一つの置換、βγでは、[1,2,3]βγ=[3,1,2]なので、
|A|では、ε(3,1,2)a1 3×a2 1×a3 2、の項に対して、
|A'|の、ε(3,1,2)a3 1×a1 2×a2 3、は、積の順序を入れ替えても同一の値にはならないが、
ε(2,3,1)a2 1×a3 2×a1 3、は、積の順序を交換すれば、青字個所は、同一の値となる。
なお、[2,3,1]=[1,2,3]γβ=[1,2,3]αγ、であり、偶順列なので、εの値も同一である。
ここでも、[2,3,1]=[1,2,3]γβ、で分かるように、[1,2,3]βγ⇒[2,3,1]の際のβγを逆に並べたものになる。
一般的に言えば、[1,2,3,・・・,n]に関するn!種類の置換をPj、j=1～n!で表し、[1,2,3,・・・,n]×Pj=[p1,p2,p3,･･,pn]と置く。また、|A'|に対しても、Qjが存在し、[1,2,3,・・・,n]×Qj=[q1,q2,q3,･･,qn]、と置くと、
Pjが恒等置換であれば、対応するQjによる項は、対角要素となり、その項同士は、等しい。
Pjが互換の場合は、対応するQjによる項の積の順序を交換すれば、2つの項は、等しいことが分かる。
Pjが複数の互換からなる置換では、Pjを構成する互換を逆順に[1,2,3,・・・,n]に適用してできるQkに対応する項同士は、積の順序を交換すれば、等しいことが分かる。いずれの場合もεの値（±1。すなわち、互換の回数をkとしたとき、(－1)^kのこと。恒等置換は、k=0と見なす）は変わらないので、結局、|A|=|A'|、が成り立つ。（赤字個所を2021/6/30に訂正）
目次へ戻る
任意の2つの行（または列）を入れ換えれば行列式の符号が変わるってことね。
2次行列式の場合、1行目と2行目の交換で上図のように明らかに符号が変わることが分かるわ。
一般の場合を考えるために3次行列式を取り上げるわよ。前節にならえば、|A|=Σε(p1,p2,p3)a1 p1×a2 p2×a3 p3、
ここで、Aの1行目と2行目を入れ替えた行列をBで表せば、|B|=Σε(q1,q2,q3)a2 q1×a1 q2×a3 q3、である。
ここで、[1,2,3]に関する6種類の置換をPj、j=1～6で表し、[1,2,3]×Pj=[p1,p2,p3]と置く。一方、Aの1行目と2行目を入れ替えた行列の行列式、|B|に対して、Qjが存在し、[1,2,3]×Qj=[q1,q2,q3]、である。
Pjが恒等置換であるとき、|A|のε(1,2,3)a1 1×a2 2×a3 3、に対応する|B|の項は、ε(2,1,3)a2 2×a1 1×a3 3、となる。ところが、ε(1,2,3)=1、であるが、ε(2,1,3)は、－1、であるため、異符号となる。
Pjが互換を含めて一般の置換のとき、対応するQkは、Pjにαを乗じたものとなる。（αは、1番目と2番目の位置を交換）、このため、εの値が異符号となる。これにより、|B|=－|A|、であることが納得していただけると思うわ。一般の場合も同様ね。
目次へ戻る
これは、その等しい二つの行を入れ換えれば、5.（2）により|A|=－|A|。ゆえに2|A|=0、よって、|A|=0、となることが分かるでしょう。例は、下図。
なお、当然、3つ以上の行または列が等しい場合も、その行列式は、ゼロとなりますよ。
目次へ戻る
これは、3次行列式を例にとって説明するけど、これは、一般のn次行列式にそのまま、拡張できるわね。
3次行列、Aの行列式は、定義から、|A|=Σε(p1,p2,p3)a1 p1×a2 p2×a3 p3、
ここで、1行目をα倍すると、a1 p1⇒α×a1 p1、となるため、|A|⇒α×|A|、となるということよ。ま、この具体例は、特に挙げなくても良いでしょう。
目次へ戻る
行列式の一つの行（または列）の各元素が二つの数の和であれば、行列式は和の各項をその行（または列）においてできる二つの行列式の和に等しい。文章では、分かりにくいと思うので、『行列と行列式』に出ている例を挙げますよ。
3次行列式の1行目の各要素がそれぞれ、2数の和として、書き表せるのであれば、その行列式の値を上の図の右辺のように2つの行列式の和として表すことができるというものなのね。気をつけて欲しいのは、a1''やa2''などは、異なる値であっても差し支えないと言うこと。直感的には、素直に納得できないと思うので、もう少し説明しますね。
もし、3.（3）で説明したように行列式の行による展開を前提に考えれば、簡単に説明が付くと思うの。3.（3）で説明した余因子を使えば、|A|=Σ(k=1～3)（a1k×余因子(1行目，k列目)）、と書けるでしょ。
上の例に適用すると、
右辺は、(a1'+a1'')×余因子(1,1)+(a2'+a2'')×余因子(1,2)+(a3'+a3'')×余因子(1,3)
={a1'×余因子(1,1)+a2'×余因子(1,2)+a3'×余因子(1,3)}
+{a1''×余因子(1,1)+a2''×余因子(1,2)+a3''×余因子(1,3)}、と展開できるんだけど、{}内を見ると、それぞれ、1行目の要素が'付きと''付きの要素である3次行列式の展開であることが分かるので、展開を元に戻すと、右辺は、
となることが納得していただけると思いますよ。
一方、行列式の定義から考えると、3次行列式の例では、|A|=Σε(p1,p2,p3)a1 p1×a2 p2×a3 p3、である。
ここで、a1 p1=a'1 p1+a''1 p1、であると仮定すれば、右辺は、
Σε(p1,p2,p3)(a'1 p1+a''1 p1)×a2 p2×a3 p3、
=Σε(p1,p2,p3)a'1 p1×a2 p2×a3 p+Σε(p1,p2,p3)a''1 p1×a2 p2×a3 p、と分解できる。
これで、必要な内容が証明されたわね。一般のn次行列式についても同様よ。
2021/7/1追記 5.（1）に従えば、行と列を交換した下図のような関係式も同様に成り立つので、注意してね。
目次へ戻る
行列式の一つの行に定数を掛けて、これを他の一つの行に加えても行列式は変わらない。列についても同じであるっていうことね。例を挙げましょう。次の図の左辺の2行目にx1をかけて、3行目から引いています。
さらに、1行目にx1をかけて、2行目から引くと、
となります。（次の（7）にある行列式の次数を下げる状態に変形できました）
そこで、まずは、この変形が正しいことが納得していただかないといけないわね。下図の3次行列式|A|で説明しましょう。
|A|の2行目×k（定数）を1行目に加えた行列式は、（文中と下図に記載していたcはkの誤り。訂正しました：2022/2/23）
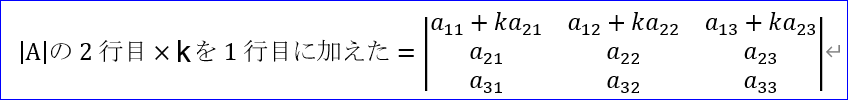
となるでしょ。これを5.（5）の性質で2つの行列式の和に分解すると、
さらに、5.（4）の『行の要素をα倍で行列式もα倍』と5.（3）の『二つの行(または列)の等しい行列式は0』を使えば、
となって、元の行列式と等しいことが分かるという寸法なのね。これで、一般のn次行列式の場合も証明できるでしょう。
目次へ戻る
（6）のように列の要素の1つ以外がすべてゼロの場合、行列式の次数を下げることができる。同様に行の1つ以外のすべてゼロの場合も、次数を下げることができるということね。前節の例では、
この右辺は、第1列が(1,1)を除くとすべてゼロなので、
と変形できることになる。
さらに言えば、右辺は、5.（4）に従って、1列目の共通因子(x2－x1)と2列目の共通因子(x3－x1)をくくり出すと、
と変形でき、右辺で、1行目にx2をかけて、2行目から引けば、
よって、与式は、
と変形できた。これは、3次の『ファンデルモンド（ヴァンデルモンド）（Vandermonde）の行列式』と言われるものである。
なお、下図の『ファンデルモンド（ヴァンデルモンド）（Vandermonde）』の転置も、5.（1）により、上の結果と同一となる。
この『行または列の1つ以外の要素がすべて0ならば、行列式の次数を下げることができる』は、3.（1）行列式の展開を考えれば、直ちに納得ができるでしょう。
もし、展開を使わない証明であれば、たとえば、下図のように、3次行列式の(1,1)が1で、それ以外の1行目の要素がすべてゼロであれば、
となるが、定義に戻り、|A|=Σε(p1,p2,p3)a1 p1×a2 p2×a3 p3、
において、a11=1、a12=a13=0、は、p1=1では、項は、ε(1,p2,p3)1×a2 p2×a3 p3、であるが、p1<>1では、対応する項がゼロとなる。従って、Σは、ε(p2,p3)×a2 p2×a3 p3、となり、p2,p3は、(2,3)のすべての順列を動く。偶順列である恒等変換E⇒(2,3)、奇順列となる互換1回⇒(3,2)、の2つしかないので、|A|は、結果として、a22×a33－a23×a32、となるという具合である。どうやら、この場合も一般的にも十分に説明可能なように思われるわ。
参考として、以下に、4次の『ファンデルモンド（ヴァンデルモンド）（Vandermonde）の行列式』を挙げましょう。
左辺で、4列－3列×x1を作ると、右辺のようになり、
3列－2列×x1、2列－1列×x1を続けると、
5.（7）を使って3次に次数を下げると
5.（4）を使って共通項をくくりだすと、
となることがわかるでしょう。
ここで、3次の行列式部分は、前例で、x3⇒x4、x2⇒x3、x1⇒x2と置き換えたものであるから、
と変形できる。これは、kとjを1～4の整数として、k>jの（xk－xj）のすべての積なので、
と簡単に書くことが可能となるのね。
一般の場合も同様である。ここでは、|D(n)|で表すことにする。もし、xkがn次方程式の根の場合は、|D(n)|の2乗が方程式の根の「判別式」を表す。判別式については、第91回『マルコフ過程（4）（非対称型道中双六：固有方程式の漸化式）』で、5次までの判別式を別な角度から計算している。
※ 判別式が|D(n)|の2乗であると判別式が常にゼロまたは正と勘違いしそうだが、n次方程式の根は、一般には、複素数なので、|D(n)|^2は、負となる場合もある。たとえば、x^2+1=0、では、x=±#i、より、|D(2)|^2=－4、一方、よく知られた2次方程式（Ax^2+Bx+C=0）の判別式は、B^2－4AC=0－4×1×1=－4、となり、当然ながら、先の結果と一致する。
目次へ戻る
作成日：2021/1/20
語句を微修正：2020/1/21～1/23
語句を微修正：2021/2/1
5（1）の誤解を与える表現を訂正：2021/6/30
5（5）に例を追記：2021/7/1
5（6）の誤りを訂正：2022/2/23
