 は~い。ともちゃんです。半年ぶりの登場ですよ。次のような例があったわ。(『行列と行列式』:古屋茂著:培風館:1970年3月増補第20刷41頁)(以下『行列と行列式』と書きます)
は~い。ともちゃんです。半年ぶりの登場ですよ。次のような例があったわ。(『行列と行列式』:古屋茂著:培風館:1970年3月増補第20刷41頁)(以下『行列と行列式』と書きます)1.はじめに
2.いろいろな行列式
(1)巡回行列式
① 3次の巡回行列式
② 2次の巡回行列式
③ 3次の巡回行列式(別解)
④ n次の巡回行列式
(2)平面上の2点を通る直線
① 行列式=0を使う
② ベクトルを使う
③ ベクトルを使って行列式=0を使う
(3)3次元空間上の2点を通る直線
(4)3次元空間上の3点を通る平面
① 行列式=0を使う
② ベクトルのスカラー3重積を使う
③ ベクトルを使って行列式=0を使う
④ ベクトルと連立方程式を使う
(5)四面体の体積
① スカラー3重積を使う
② 多面体の体積公式を使う
③ 多面体の体積を計算するExcelブック
(6)ファンデルモンドの行列式
① ファンデルモンド(Vandermonde)
② 定義と展開
③ DERIVEによる計算
④ 判別式
⑤ 判別式と対称式
3.行列の対角化
(1)3次の巡回行列
① 固有値と固有ベクトル
② 複素ベクトルと複素内積
③ 3次の巡回行列の対角化
④ ユニタリ行列とユニタリ変換
⑤ DERIVEのAPPEND関数等
(2)行列の対角化
① 対角化とご利益
② エルミート行列
③ 正規行列
④ 一次変換で対角化可能な行列
⑤ 正規行列でなく対角化もできない行列
⑥ 固有ベクトルが少なく対角化できない行列
⑦ 非対称道中双六のマルコフ行列
4.行列・行列式の性質(続)
(1)行列の積の行列式
① 2次行列
② 行列の積から考える行列式とは?
(2)逆行列
① 逆行列の定義
② 行列と逆行列の積の順序
③ 逆行列の逆行列は元の行列
④ 逆行列の転置は転置行列の逆行列
⑤ 2つの行列の積の逆行列
⑥ 逆行列の行列式
(3)フロベニウスの定理
① フロベニウスの定理
② 2次行列
③ 3次の巡回行列
(4)ケーリー・ハミルトンの定理
① ケーリー氏、ハミルトン氏
② 2次行列
③ ケーリー-ハミルトンの定理による逆行列の計算
④ 逆行列を計算するDERIVEのユーザー定義関数
⑤ ユーザー定義関数の計算例
今回は、第98回の『行列式(2)』の続きです。特徴的な行列式、行列の対角化、逆行列を含む行列と行列式の性質(続)をご紹介しています。では、ともちゃん、どうぞ!
※ テキストの数式内の半角の「ハイフン・マイナス記号」(-)は、べき乗(A^-1、の-1など)を除き、全角のハイフン(-)に置き換えてあります。また、DERIVEで乗算を意味するドット(·)も、画像以外では、その多くを省いています。ご留意下さい。
目次へ戻る
これまで、ファンデルモンド(ヴァンデルモンド)(Vandermonde)の行列式やヒルベルト行列の行列式について、触れてきましたが、この章では、あらためて、いくつかの行列式を取り上げてみましょう。
 は~い。ともちゃんです。半年ぶりの登場ですよ。次のような例があったわ。(『行列と行列式』:古屋茂著:培風館:1970年3月増補第20刷41頁)(以下『行列と行列式』と書きます)
は~い。ともちゃんです。半年ぶりの登場ですよ。次のような例があったわ。(『行列と行列式』:古屋茂著:培風館:1970年3月増補第20刷41頁)(以下『行列と行列式』と書きます)
上の左辺の行列式は、1行目の内容(a,b,c)が2行目では、右に1列シフト、はみ出した3列目が2行目の1列目に移動して(c,a,b)となるような3つの変数が循環する行列式ね。これを「3次の巡回行列式」と呼びます。行または列に着目すれば、a→c→b→a と辞書の降順に循環しています。
なお、行列式で2行目と3行目とを交換すれば、符号が変わるので、次のようになります。
こちらは、a→b→c→aと辞書の昇順に循環していますね。
目次へ戻る
2次の巡回行列式は、次のようになるわ。
ここで、最右辺の±1は、z^2=1の解。なんで?って思うけど、この考え方は、重要で、3次の場合に適用すれば、次の③の別解となります。
目次へ戻る
行列式の値をDとして、
ここで1列目と2列目を3列目に加算すると、3列目が同一のa+b+cとなるので、
と書き表せることが分かるでしょ。ちなみに、Xは、下図のように、a,b,cについて、2次の同次式だけど、
②の例にならい、z^3=1の解を使って、Xが(a+bz+cz^2)×(a+bz^2+cz)、と因数分解できないかと考える。そのために、Dの計算値と等値して、X=(a^2-a(b+c)+b^2-bc+c^2)、を作れば、zの4次方程式になるけど、解の中で、a,b,cに依存しない解は、次の2つだけ。
これら2根とも、1の3乗根の一つをω=-1/2+(√3#i)/2、と表した時、z=ωまたは(共役複素数の)ω^2となっていることが分かる。(残るひとつは、ω=1)、ここで、i
は、虚数単位とする。(DERIVEでは、#i と入力可能なので、以下でも、#i と書くことがあるわよ。)
これで、Xは、
と因数分解されることが分かった。
それで、Dは、結局、下図のように因数分解される。
でも、『X=(a+bz+cz^2)×(a+bz^2+cz)と書けないかと考える』は、少し、飛躍があるわね。答えから、構成しているような気持ち悪さが残るわ。そこで、古屋先生のご本では、Dに(a+b+c)以外の因子があるかどうかを次のように調べています。
a+b+cの因子をくくりだしたように、(ここが天下り式ではあるけど)、ωを1の3乗根として、2列×ωと3列×ω^2を1列目に加えると、
となる。ただし、上式の右端の行列式で、2行1列、3行1列のω、ω^2でくくる個所は、ωの性質(ω^3=1)を利用しています。これを見ると、Dが、(a+bω+cω^2)も共通因子として持つ事が分かるでしょ。
同様に、2列目×ω^2と3列目×ωを1列目に加えると、
従って、Dは、(a+bω^2+cω)も共通因子に持つ事が分かるのね。結局、Dは、
となり、Dが3次同次式であるため、a,b,c に依存しない定数は、a^3の係数が1であることから、定数=1、となる。
このように、一見、唐突に登場した1の3乗根だけど、DERIVE的には、
D=a^3+b^3+c^3-3abc=(a+b+c)(a^2-a(b+c)+b^2-bc+c^2)、において、
2番目のかっこ内の式をaの多項式として、 DERIVEにより、複素数の範囲内で因数分解すると、
(a^2-a(b+c)+b^2-bc+c^2)=a-(b+c)/2+√3ABS(b-c)/2)(a-(b+c)/2-√3ABS(b-c)/2
ここで、今、b>=cと仮定すると、
=(a-(b+c)/2+√3(b-c)/2)(a-(b+c)/2+√3(c-b)/2)
=(a+b(-1/2+√3#i/2)+c(-1/2-√3#i/2))(a+b(-1/2-√3#i/2)+c(-1/2+√3#i/2))
=(a+bω+cω^2 )(a+bω^2+cω)
また、b<cの場合は、2つのかっこの順序が入れ替わるだけで、両者の積は、変わらないことが分かる。
このよう考えれば、ここに、1の3乗根が登場してくる理由が納得できると思うわ。
※対称式との関係
3次の巡回行列式は、対称式でもあるのね。基本対称式をs1,s2,s3 とすれば、s1=a+b+c、s2=ab+bc+ca、s3=abc、だけど、
D=a^3+b^3+c^3-3abc、を基本対称式で表すと、D=s1^3-3s1s2=s1(s1^2-3s2)、となる。こうしてみても、s1(=a+b+c)が共通因子であることが分かる。
目次へ戻る
『行列と行列式』では、3次の場合を拡張して、n次の巡回行列式も1のn乗根ωにより、要素の1次式のn個の積に因数分解されることが記されている。導き方は、原理的には、n=3と同様なので、ここでは、n=5の場合を数値計算から検証してみましょう。
ここで、5次の巡回行列を下図のようにAと置く。
DERIVEで、行列式の値をDET(A)と計算し、結果をx1の関数とみて、g(x1)と定義しますね。
g(x1)に一次因子(x1-α)があるか否かは、『整式に関する剰余の定理』により、余り(剰余)=f(α)=0、となるかで判定できる。(αは、一般には、複素数)。
ここで、新規に関数、f(n)を次のように定義すると、
g(x1)が(x1+x2+x3+x4+x5)で割り切れるか否かは、x1が、
となるx1に対して、g(-f(0)+x1)がゼロとなるかどうかで判定できる。計算結果は、0となることが分かった。
さらに、w^5=1を解いて、
w=-√5/4-1/4-√(10-2√5)/4∨w=-√5/4-1/4+√(10-2√5)/4∨w=√5/4-1/4-√(2√5+10)/4∨w=√5/4-1/4+√(2√5+10)/4∨w=1、が得られるので、
同様に、n=1~4について、g(-f(n)+x1)を計算すると、やはり、ゼロとなる。これらのことから、
D(5)=g(x1)=定数×f(0)*f(1)*f(2)*f(3)*f(4)、が分かる。
さらに、D(5)で、x1の係数を考えれば、定数=1であることも明らか。
よって、D(5)が要素と1の5乗根により、右辺のように因数分解されることが検証されたわね。
とは言っても、上述のような方法は、実は、『巡回行列式』であることが分かっているから可能なのであり、いきなり、多項式を示されても、因数分解は、困難でしょう。
また、x1をxとし、x2~x5を実数に適宜、置き換えれば、代数方程式の数値解法の例題ができます。
例:
上の行列式は、展開すると、x^5 + 135x^3 + 3890x^2 + 31795x + 107288=0、となります。
DERIVEの数値解法では、瞬時に下記の解が得られます。(計算精度10桁)
(x = 8.708203932 - 15.66593223 ∨ x = 8.708203932 + 15.66593223 ∨ x = -4.708203932 - 4.424767466 ∨ x = -4.708203932 + 4.424767466 ∨ x = -8)、
一方、前述のf(n)で、x1=x、x2=3、x3=6,x4=-8、x5=7と置いて、-f(n)+xをn=0~4まで計算すると
([-8, 3√5 + 2 - √(202√5 + 530)/2, - 3√5 + 2 - √(530 - 202√5)/2, - 3√5 + 2 + √(530 - 202√5)/2, 3√5 + 2 + √(202√5 + 530)/2])
w=(- √5/4 - 1/4 - √(10 - 2√5)/4)と置けば、(w=1以外の2根のいずれでも一緒)
([-8, 3√5 + 2 - √(202√5 + 530)/2, - 3√5 + 2 - √(530 - 202√5)/2, - 3√5 + 2 + √(530 - 202√5)/2, 3√5 + 2 + √(202√5 + 530)/2])
近似値を求めると、10桁の計算精度で、
([-8, 8.708203932 - 15.66593223, -4.708203932 - 4.424767466, -4.708203932 + 4.424767466, 8.708203932 + 15.66593223])となり、数値計算の結果と末尾まで一致していることが分かる。
もっとも、5次巡回行列式の場合は、DERIVEでも(x1+x2+x3+x4+x5)を因子としてくくり出せるので、実質的に上記の方程式は、xの1次式×4次式に分解されて、数値計算されていると思われるので、十分に正確な近似値がでるのは、当然と言えば当然ね。
目次へ戻る

これは、『行列と行列式』の47頁の例題にあります。
下図のように、平面上の2点、P1とP2とを結ぶ直線上の任意の位置にある点、P(x,y)を表す関係式を求める。
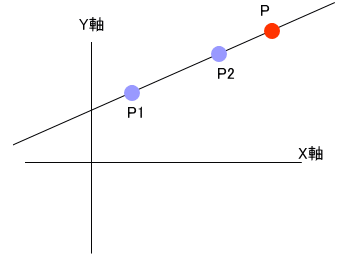
平面上の2点、P1(x1,y1)とP2(x2,y2)とを結ぶ直線の方程式を、a x+b y+c=0、と置けば、
Pをこの直線上の任意の点[x,y]、として、P、P1、P2が方程式を満たす条件、
a x +b y +c=0
a x1+b y1+c=0
a x2+b y2+c=0
これらの3つの関係は、行列とベクトルを使って、以下のように書き表される。
すべてがゼロではない a、b、c、に対して、上式が成立するためには、左辺の3次行列の行列式がゼロとなる必要があるのね。
よって、
これから、おなじみの関係式が得られます。
目次へ戻る
ベクトルを知っている場合は、以下のようにベクトルを使うでしょう。
P(x,y)をP1とP2を結ぶ直線上の点として、
P1からPへのベクトル、P1→Pは、[x-x1,y-y1]、P1→P2は、[x2-x1,y2-y1]というベクトルで書き表せるけど、
P1→Pは、P1→P2の任意の実数倍であることから、パラメーターをtと置けば、
[x-x1,y-y1]=t×[x2-x1,y2-y1]が成り立つ。
これから、x=x1+t×(x2-x1)、y=y1+t×(y2-y1)、で[x,y]の位置を計算できる。
なお、t を消去するには、第1式×(y2-y1)-第2式×(x2-x1)を作り、
(y2-y1)x-(x2-x1)y=x1×(y2-y1)-y1×(x2-x1)
よって、
(y2-y1)x-(x2-x1)y=x1y2-y1x2、移項して、
(y2-y1)x-(x2-x1)y+y1x2-x1y2=0、が得られる。
目次へ戻る
ベクトルを使うけど、途中から、次のように行列式と結びつけることも可能かも。
x-x1-t×(x2-x1)=0、y-y1-t×(y2-y1)=0、から、
を得る。
目次へ戻る

3次元空間の直線を考えると、
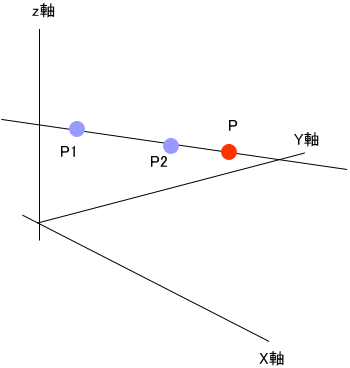
と図示できる。2次元平面上の直線は、(2)のように ax+by+c=0、という一つの式で書き表されるけど、3次元空間上の2点、P1(x1,y1,z1)とP2(x2,y2,z2)とを結ぶ直線の方程式は、一つの式では、書けないわよ。
これを、ax+by+cz+d=0、と勘違いしやすいけど、この式は、3次元空間上の平面を表す式なのよね。
ベクトルを使うと、(2)②と同様に、P(x,y,z)がP1とP2を結ぶ直線上の任意の点として、
P1→Pは、[x-x1,y-y1,z-z1]、P1→P2は、[x2-x1,y2-y1,z2-z1]のベクトルとなる。
P1→Pは、P1→P2の任意の実数倍であることから、パラメーターをtと置けば、
[x-x1,y-y1,z-z1]=t×[x2-x1,y2-y1,z2-z1]が成り立つ。
これから、x=x1+t×(x2-x1)、y=y1+t×(y2-y1)、z=z1+t×(z2-z1)、ということになります。
ま、このようにパラメーターを使うと見通しが良くなるわね。
t を消去することもできるけど、1つの式には、まとめられないのが残念。
目次へ戻る
3次元空間内の平面を下図のように図示します。
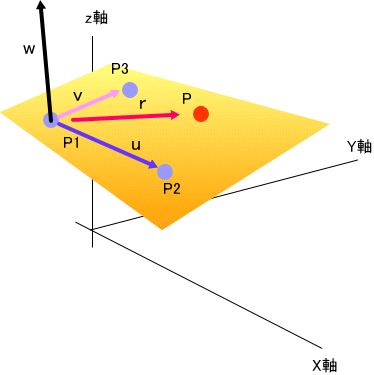

3次元空間の平面は、相異なる3つの点(3点がすべて同一直線上にはない)P1、P2、P3が決まれば、一意に定まります。
お待たせしました。この平面の方程式が、ax+by+cz+d=0、となりますよ。
PをP1、P2、P3と同一平面上の任意の点[x,y,z]、として、これら4点が同一平面上にある条件、
a x1+b y1+c z1+d=0
a x2+b y2+c z2+d=0
a x3+b y3+c z3+d=0
を含めて、4つの関係式は、以下のようにも書き表される。
すべてがゼロではないa、b、c、dに対して、上式が成立するためには、左辺の4次行列の行列式がゼロとなる必要がある。従って、
となって、方程式の4つの係数、aは、赤字、bは、青字、cは、緑字、dは、紫字として求められた。(あーしんど!)
目次へ戻る
P1→P2とP1→P3をu、vとベクトルで表し、P1→Pをrとすれば、r=[x-x1,y-y1,z-z1]、
P1→P2は、u=[x2-x1,y2-y1,z2-z1]、
P1→P3は、v=[x3-x1,y3-y1,z3-z1]というベクトルとなる。

ここで、要領の良い方法として、「スカラー3重積」、u×v(ベクトル積)とrとの内積を作り、これが直交する(内積がゼロ)ことを利用することね。
i、j、k を直交座標の単位ベクトルとすれば、u×vは、形式的に3次行列式により次のように記される。
直交条件は、スカラー3重積=0から、
これで求める式が得られたわ。
目次へ戻る
②のuとvで作られる平面上の任意の点をPとして、P1→P=r=s u+t v、
ここで、s、tは、任意の実数のパラメーター、とすれば、よいでしょう。
[x-x1,y-y1,z-z1]=s[x2-x1,y2-y1,z2-z1]+t[x3-x1,y3-y1,z3-z1]
すなわち、
x-x1= s(x2-x1)+ t(x3-x1)
y-y1= s(y2-y1)+ t(y3-y1)
z-z1= s(z2-z1)+ t(z3-z1)
これは、
これで、
から、同一の結果を得ることもできるでしょう。
目次へ戻る
オーソドックスには、③の途中まで同じだけど、
x-x1= s(x2-x1)+ t(x3-x1)、
y-y1= s(y2-y1)+ t(y3-y1)、
z-z1= s(z2-z1)+ t(z3-z1)、
の下の2式からs、tを求めて、
[s = - (y(z1 - z3) + z(y3 - y1) + y1z3 - y3z1)/(y1(z2 - z3) + y2(z3 - z1) + y3(z1 - z2)) ∧ t = (y(z1 - z2) + z(y2 - y1) + y1z2 - y2z1)/(y1(z2 - z3) + y2(z3 - z1) + y3(z1 - z2))]
これを第1式、x-x1= s(x2-x1)+ t(x3-x1)、に代入して整理する。
x(y1(z2 - z3) + y2(z3 - z1) + y3(z1 - z2)) - y(x1(z2 - z3) + x2(z3 - z1) + x3(z1 - z2)) + z(x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)) + x1(y3z2 - y2z3) + x2(y1z3 - y3z1) + x3(y2z1 - y1z2) = 0
当然ながら、同一の結果となります。
目次へ戻る

3次元空間内の四面体(三角錐)の体積は、行列式でも、表すことができる。
ここでは、『行列と行列式』の92頁を参考に少し変更したわ。
上図のようなP1、P2、P3、P4の4点を結ぶ四面体の体積 Vは、
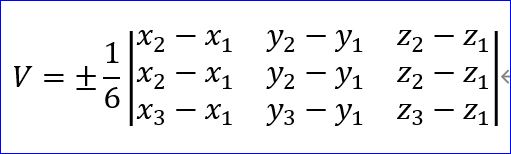
で与えられる。
(図中のy3-y1をy3-x1と誤記していました。お詫びして訂正します。2022/4/12)
目次へ戻る
スカラー3重積を使うのが一番分かりやすいと思うわ。
ベクトルを使って、P1→P2=u、P1→P3=v、P1→P4=w、と置きます。
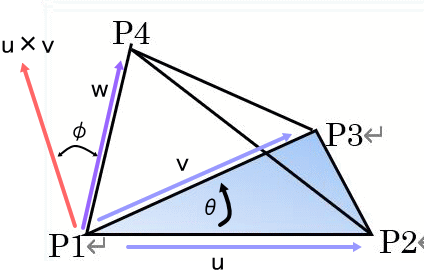
赤線で示すu×vは、uからvに右ネジを回す時ネジが進む方向を持つ底辺に垂直方向のベクトル。
その大きさは、|u×v|=|u||v|sin(θ)、θは、uとvのなす角度。
右辺は、底辺の薄い青色の三角形(P1-P2-P3)の面積の2倍にあたります。
一方、P1→P4=wとu×vとのなす角度をφと置けば、u×vとwとの内積は、
(u×v)・w=底辺の面積の2倍×|w|cos(π/2-φ)
=底辺の面積の2倍×|w|sin(φ)
=底辺の面積の2倍×P4から底辺に下ろした垂線の長さ(三角錐の高さ)
=三角錐の体積の6倍
最後で、三角錐の体積=1/3×底辺の面積×三角錐の高さを使った。
従って、
w=[x4-x1,y4-y1,z4-z1]、
よって、(u×v)・wは、
従って、体積Vは、
となる。
※ ±(プラスマイナス)(あるいは絶対値を取る)のは、u×vの方向とwとの方向が同一方向ならば、Vが正となるが、逆方向にとった場合は、負となるための用心です。
目次へ戻る
多面体の体積公式は、『DERIVE deドライブ』の第61回『多面体の体積公式』あるいは、第76回『多角形及び多面体の重心と高次のモーメント(2)』に下記のように記しています。
多角形の面を持つ任意の面数の多面体の体積、Vは、
V=(1/3)Σ(各面の和)(r1・S)、で与えられる。
ここで、Sは、各面の面積ベクトル(S=(1/2)Σ(i=1~n)(ri×ri+1))、
r1は、各面の多角形の任意の頂点の位置ベクトル、
riは、r1から番号付けした各頂点の位置ベクトル、
nは、各面の頂点の総数、
r1、ri、nは、一般的に面毎にそれぞれ異なる。
多角形の頂点番号は、多面体の外から面を見て反時計回り(多面体の内部から見て外部に右ネジが進む方向)にr1からi=2~nと割り振る。
ただし、n+1は、1と見なす。
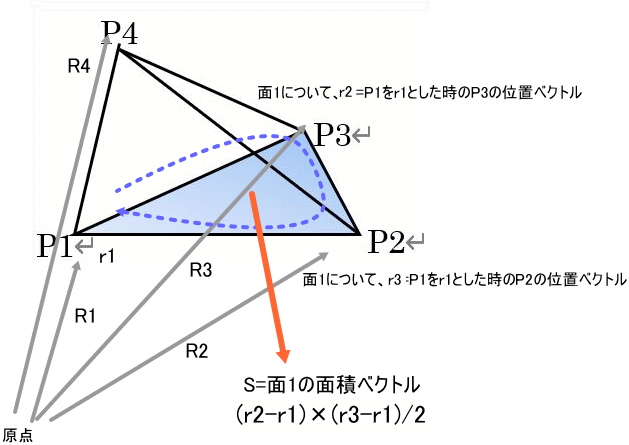
今回の四面体の場合は、次のような4つの面がある。
(Oは、座標原点。以下で単にO→P1等をP1と書いている個所があるわよ)
面1=P1→P3→P2、r1=O→P1、r2=O→P3、r3=O→P2とする。
(面1のr1は、P1でなくても、P2やP3から始めてもよい。そのときは、r2=O→P1、r3=O→P3となる。以下同様)
面2=P2→P3→P4、r1= O→P2とする。
面3=P1→P4→P3、r1= O→P1とする。
面4=P1→P2→P4、r1= O→P1とする。
上図のように、R1~R4を頂点の絶対位置を表す位置ベクトルとして、面毎に可変な r1~r3とは別に定義しておいて、計算を進めると分かりやすいでしょう。すなわち、O→P1≡R1=[x1,y1,z1]等と置きます。
面1:S=(1/2)(R1×R3+R3×R2+R2×R1)= ([- (y1(z2 - z3) + y2(z3 - z1) + y3(z1 - z2))/2, (x1(z2 - z3) + x2(z3 - z1) + x3(z1 - z2))/2, - (x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2))/2])
S・r1=S・R1=(- (x1(y2z3 - y3z2) + x2(y3z1 - y1z3) + x3(y1z2 - y2z1))/2)
面2:S=(1/2)(R2×R3+R3×R4+R4×R2)=([(y2(z3 - z4) + y3(z4 - z2) + y4(z2 - z3))/2, - (x2(z3 - z4) + x3(z4 - z2) + x4(z2 - z3))/2, (x2(y3 - y4) + x3(y4 - y2) + x4(y2 - y3))/2])
S・r1=S・R2=((x2(y3z4 - y4z3) + x3(y4z2 - y2z4) + x4(y2z3 - y3z2))/2)
面3:S=(1/2)(R1×R4+R4×R3+R3×R1)= ([- (y1(z3 - z4) + y3(z4 - z1) + y4(z1 - z3))/2, (x1(z3 - z4) + x3(z4 - z1) + x4(z1 - z3))/2, - (x1(y3 - y4) + x3(y4 - y1) + x4(y1 - y3))/2])
S・r1=S・R1= (- (x1(y3z4 - y4z3) + x3(y4z1 - y1z4) + x4(y1z3 - y3z1))/2)
面4:S=(1/2)(R1×R2+R2×R4+R4×R1)= ([(y1(z2 - z4) + y2(z4 - z1) + y4(z1 - z2))/2, - (x1(z2 - z4) + x2(z4 - z1) + x4(z1 - z2))/2, (x1(y2 - y4) + x2(y4 - y1) + x4(y1 - y2))/2])
S・r1=S・R1= ((x1(y2z4 - y4z2) + x2(y4z1 - y1z4) + x4(y1z2 - y2z1))/2)
体積は、多面体の体積公式に従い、面1~面4毎のS・r1を加算し3で割ると、
V= (- (x1(y2(z3 - z4) + y3(z4 - z2) + y4(z2 - z3)) - x2(y1(z3 - z4) + y3(z4 - z1) + y4(z1 - z3)) + x3(y1(z2 - z4) + y2(z4 - z1) + y4(z1 - z2)) - x4(y1(z2 - z3) + y2(z3 - z1) + y3(z1 - z2)))/6)、が得られる。
なお、この式と①のスカラー3重積から導いた体積との一致は、差し引きゼロとなることで確認できました。
※ 四面体の場合は、①のスカラー3重積による導き方が明らかに簡明ですが、②の方法は、5面以上の面を持つどのような多面体でも一般に適用できます。(富士山の体積も原理的には求められますよ)
目次へ戻る
座標値が数値で与えられている場合、『自作ものコーナー』にアップしてあるExcelブック、『TamentaiVer2.xlsm』を使うと便利です。ここの四面体の例でご説明しますね。
P1(3,-2,5)、P2(7,10,8)、P3(5,15,9)、P4(4,6,25)、としましょう。Excel表の頂点リストに下図のように上の4点の座標値を入力します。
ちなみに、頂点リストには、100点まで入力できます。(利用しない頂点リストのセルは、Deleteで空白としておきます。ゼロではありません。)
次に先に挙げた面の頂点の順番は、次のようでした。面1=P1→P3→P2、面2=P2→P3→P4、面3=P1→P4→P3、面4=P1→P2→P4、これを面毎に「頂点リストの頂点No.を列記」の欄に下図のように入力します。(頂点リストの頂点No.を並べる順番は、外から見て反時計回りであれば、どの頂点No.から始めても差し支えありません。例えば、下図では、面1は、1→3→2としていますが、3→2→1、あるいは、2→1→3としてもよい。ただし、利用しないセルは、空白です。ゼロではありません。)
ちなみに、面の数は、100面まで、面毎の多角形の頂点総数は、20個まで指定できます。最後に「実行」ボタンをクリックします。これにより、下図のように面数、体積、重心の位置座標(Gx、Gy、Gz)が表示されます。
※ 先の式の計算結果に数値を代入して計算した体積の厳密値、797/6≒(132.8333333)、であり、Excelの計算値を小数点以下最大桁まで表示しても、一致していることが分かります。
目次へ戻る

ファンデルモンド(ヴァンデルモンド)氏は、ウィキペディアによれば、18世紀のフランスの数学者、音楽家、化学者です。1735年2月28日~1796年1月1日。
目次へ戻る
n次のファンデルモンドの行列式を|D(n)|と書くことにすると、n=5では、下図のようになる。
第97回『行列式(1)』ですでに示しているように
と表される。一般のnの場合も同様に導くことができる。
すなわち、
である。
目次へ戻る
ファンデルモンド行列式の右辺をDERIVEで計算する場合は、V:=VECTOR(x↓k,k,1,n)、と外部で定義しておく。
例えば、n=10であれば、演算後は、V=[x↓1,x↓2,x↓3,x↓4,x↓5,x↓6,x↓7,x↓8,x↓9,x↓10]、となる。
ファンデルモンドの行列式|D(n)|をここでは、便宜的にDERIVE上で、D2(n)として下式のように関数定義すれば。
D2(n):=∏(∏(IF(k_>j_,V↓k_-V↓j_,1),j_,1,n),k_,1,n)、
これで、n=1~10までの|D(n)|を計算できる。
D2(5)=(x↓2-x↓1)(x↓3-x↓1)(x↓3-x↓2)(x↓4-x↓1)(x↓4-x↓2)(x↓4-x↓3)(x↓5-x↓1)(x↓5-x↓2)(x↓5-x↓3)(x↓5-x↓4)、となる。
※ 下向き矢印 ↓は、DERIVEの添え字を表す記号。
※Vector関数を使わずに、V:=[x1,x2,x3,x4,x5,x6,x7,x8,x9,x10]と定義しても、もちろんよい。ただし、nが大きくなると手入力するのが面倒では、ある。(このように定義した場合は、前述のx↓2
は、x2などとなる)
ところで、|D(n)|の展開、
この証明として第97回で挙げた以外の別解法は、次の通りです。(『行列と行列式』)
『与えられた行列式を|D(n)|とする。行列式の定義によって|D(n)|がx1、x2等の多項式であることは、明白である。xk=xjとおけば第k列と第j列とが一致するから|D(n)|=0となり|D(n)|は(xk一xj)で割り切れることがわかる。k、j(k≠j)は、任意であるから、|D(n)|は、Π(k>j)(xk一xj)で割り切れることになり、|D(n)|=f(x1,x2,・・xn)×Π(k>j)(xk-xj)と書ける.この両辺の次数は共に1+2+……+(n-1)=n×(n-1)/2である。f(x1,x2,・・xn)であるが、両辺のx2x3^2x4^3・・・xn^(n-1)、の係数を比べれば、f(x1,x2,・・xn)=1となる。これで、|D(n)|=Π(k>j)(xk-xj)となることが分かった。』
※注意1
『xk=xjとおけば第k列と第j列とが一致するから|D(n)|=0』は、『行列式(1)』の5.(3)『同一の値を持つ列または行があるときは、その行列の値は、ゼロとなる』による。
※注意2
『両辺のx2x3^2x4^3・・・xn^(n-1)、の係数を比べれば、定数=1』の点について。
行列式|A|の定義によれば、|A|=Σε(p1,p2,・・pn)a1p1×a2p2×・・×anpn、ak等は、行列Aの要素。
ここで、Σは、(1,2,・・n)という数の並び(順列)について、2つの要素を入れ替える操作(互換)を複数回行ってできる順列を(p1,p2,・・・pn)としたとき、すべての異なる順列に関する和をとる。また、εは、その順列が『偶順列』であれば、+1を、『奇順列』のときは、-1をとる関数とする。なお、『偶順列』とは、偶数回(ゼロ回も含む)の互換を行うことで得られる順列、『奇順列』とは、奇数回の互換を行うと得られる順列である。全体の個数は、n個のすべての並びの個数、すなわち、n!個であり、その半数が偶順列、残りが奇順列となる。
この定義を|D(n)|に使うと、|D(n)|=Σε(p1,p2,・・pn)(x1p1)^0×a2p2×・・×anpn、左辺の|D(n)|のx2x3^2x4^3・・・xn^(n-1)は、定義から、行列の左上から右下までの対角要素の積なので、Σa1^0×a2^1×a3^2×・・×an^(n-1)、となり、この係数が1となるから。
目次へ戻る
第97回では、上記のx1~xnがn次の代数方程式(最高次の係数が1のもの)の根であるならば、|D(n)|^2は、その方程式の判別式になることに触れていた。以下、やや、繰り返しになるが、記しておきましょう。
|D(n)|^2の右辺をDERIVEで計算する方法は、|D(n)|と同様に、V:=VECTOR(x↓k,k,1,n)、と外部で定義する。
例えば、n=10であれば、演算後は、V=[x↓1,x↓2,x↓3,x↓4,x↓5,x↓6,x↓7,x↓8,x↓9,x↓10]、となる。
判別式|D(n)|^2を便宜上、DERIVE上では、D1(n)と書いて、下のように関数定義すれば、
D1(n):=∏(∏(IF(k_=j_,1,V↓k_-V↓j_),j_,1,n),k_,1,n)、として、
n=1~10までの|D(n)|^2を計算できる。
たとえば、|D(5)|^2=D1(5)
=(x↓2-x↓1)^2(x↓3-x↓1)^2(x↓3-x↓2)^2(x↓4-x↓1)^2(x↓4-x↓2)^2(x↓4-x↓3)^2(x↓5-x↓1)^2(x↓5-x↓2)^2(x↓5-x↓3)^2(x↓5-x↓4)^2
※注意 判別式の定義のとおりに計算する場合、定義に方程式の根 xi が陽に含まれている。しかし、nが5以上では、根の公式が一般には、存在しないため、判別式の値を計算できない。また、n=3、4でも、計算が複雑になることから、対称式を基本対称式に分解するのが得策である。
目次へ戻る
対称式は、第93回『マルコフ過程(6)(非対称型道中双六:平均日数と対称式)』で取り上げているけど、ここで、その要点を再掲します。
『対称式』とは、x1等の変数の番号の任意の入れ替えで不変な値を持つ式のことね。例えば、x1+x2は、x1とx2を交換しても、その式の値は、変わらない。また、x1*x2も同様である。判別式の定義式を見ると、x1とx2を交換しても、式の値は、変わらない。これ以外の組み合わせでも同様であることから、右辺は、『対称式』であることが分かる。
一方、『対称式は、基本対称式の多項式として表せ、その表し方は、一意である』という代数学の基本定理があるので、代数方程式をf(t)=0の形に書き換えてみる。
f(t)=(t-x1)(t-x2)・・・(t-xn)
=t^n+s1×t^(n-1)+s2×t^(n-2)+・・+sn、(項の数は、n+1個である。)
f(t)の2行目の式で、skは、基本対称式である。k=1~n。その具体的な表現は、s1=x1+x2+・・・+xn、s2=x1x2+x1x3+・・+x1xn+x2x3+・・sn=x1x2x3・・xn、となる。
すなわち、skは、x1・・xnからk個の相異なる変数の組み合わせの積和である。さらに、skは、元の代数方程式(最高次の係数が1のもの)の係数そのものであることに注意すれば、skは、方程式の係数のみで表せることが分かる。よって、原理的には、判別式の計算は、|D(n)|^2の右辺を基本対称式に分解すれば、方程式の根を用いずに、方程式の係数のみで表せることが分かる。
目次へ戻る

3次の巡回行列式の行列、A を例にして、行列の対角化について、考えましょう。
目次へ戻る
3次巡回行列の固有値を求める固有方程式は、固有値をλで表すと、
ここで、Iは、単位行列。この方程式は、3次巡回行列式Dのaをa-λで置き換えたものだから、
となる。よって、固有値は、λ=a+b+c、a+bω+cω^2、a+bω^2+cω、となりますよ。
3つの固有値に対応する固有ベクトルV(縦ベクトル)は、下の関係を満たす必要があるのね。
λ=a+b+c、に対するVは、V1=[1,1,1]’である。(‘は、転置を示す)
同様に、λ=a+bω+cω^2に対するV2は、
これが成り立つことは、左辺-右辺を作ると、ω^3=1を使って、
となることから分かる。
同様に、λ=a+bω^2+cωに対するV3は、
やはり、左辺-右辺を作って、ω^3=1を使うと、
と明らか。
目次へ戻る
3次の巡回行列の固有ベクトル、V1、V2、V3は、お互いの『複素内積』(すぐ後で述べる)がゼロとなります。(直交性)
V1等のベクトルは、その要素が複素数のため、『複素内積』の計算は、実数を要素とするベクトルの内積計算と同一では、ありません。複素内積(V、U)は、V・U*と定義されています。
ただし、この ・ は、実ベクトルの内積と同一の計算規則に従う演算記号とし、U*は、Uの各要素をその共役複素数で置き換えた共役ベクトルを表すものとします。
複素数を要素に持つ2次元の複素ベクトルをV=[v1,v2]、U=[u1,u2]として、(要素のv1、u1等が複素数)
・加法:V+U=[v1+v2,u1+u2]
・加法の交換:V+U=U+V
・定数の乗算:αV=[αv1,αv2]、αは、複素数
以上は、実数を要素とするベクトルと同一。
だけど、複素ベクトルの内積は、前述のように実ベクトル同士の内積の定義を拡張して、
複素内積(V,U)=V・CONJ(U)=v1×CONJ(u1)+v2×CONJ(u2)、とする必要があるのね。
ここで、CONJ(複素ベクトル)は、複素ベクトルの各要素の共役複素数を持つ複素ベクトル。
ただし、CONJ()は、DERIVEの関数。
※ 数学では、下図のようにバーを変数の上に付けて複素共役を表すことも多いけどWebでは、記載しづらいわ。
一方、物理などでは、右肩に*(アスタリスク)を付けることが多いので、ここでは、それを利用します。でも、必要に応じて、CONJ関数も使うわよ。
そもそも、なぜ「複素内積」の定義を見直す必要があるのか? と思うでしょう。
そこで、あらためて、要素が実数の(実)ベクトルの内積の性質を考える。
本節では、『行列と行列式』以外に『理数アラカルト』(https://risalc.info/)のサイトを参考にさせていただきました)
要素が実数の実ベクトルの内積演算(・)には、a,b,cを実ベクトルとした時、次の性質がある。
・交換性:a・b=b・a
・線形性:a・(αb)=α×a・b、ここで、αは、実定数
・結合性:a・(b+c)=a・b+a・c、
・正定値性:a・a>=0、
a・a=0、ならば、a=0、(逆も成立)
複素ベクトルを対象とした「複素内積」でも、実ベクトルの内積の性質をできるだけ継承していきたいと考える。
だけども、「正定値性」を満足するためには、実ベクトルの内積と同一の計算規則のままだと、うまくいかないことが分かります。
それは、V=[α+β#i,γ+δ#i]、(α~δは、実定数)とした場合、
複素ベクトルVとV自身との内積は、実ベクトルと同じ計算だと、
V・V=[α+β#i,γ+δ#i]・[α+β#i,γ+δ#i]=α^2-β^2+2(αβ+γδ)#i、と一般に複素数になるので正定値性を満足させられない。
そこで、「複素内積」を、複素内積(V,V)=[α+β#i,γ+δ#i]・[α+β#i,γ+δ#i]*、と再定義すれば、複素内積(V,V)=[α+β#i,γ+δ#i]・[α-β#i,γ-δ#i]=α^2+β^2+γ^2+δ^2、となり、この値は、実数、かつ、正またはゼロとなるため、うまくいく。
また、V=0であれば、その複素内積は、ゼロで、複素内積がゼロの場合にのみV=0であることも分かるので、正定値性を満足させられることが分かる。
ただし、DERIVEの内積演算(・)においては、複素ベクトルの場合も複素内積と同様の定義に従って計算されている。
では、「複素内積」の交換性については、どうか?
V=[α+β#i,γ+δ#i]、U=[α'+β'#i,γ'+δ'#i]、(α~δ、α'~δ'は、実定数)として、
複素内積(V,U)=[α+β#i,γ+δ#i]・[α’+β’#i,γ’+δ’#i]*
=[α+β#i,γ+δ#i]・[α’-β’#i,γ’-δ’#i]
=(αα’+ββ’+γγ’+δδ’)+(α’β-αβ’+γ’δ-γδ’)#i
一方、VとUを交換した複素内積は、
複素内積(U,V)=[α’+β’#i,γ’+δ’#i]・[α+β#i,γ+δ#i]*
=[α’+β’#i,γ’+δ’#i]・[α-β#i,γ-δ#i]
=(α’α+β’β+γ’γ+δ’δ)+(-α’β+αβ’-γ’δ+γδ’)#i
=(α’α+β’β+γ’γ+δ’δ)-(α’β-αβ’+γ’δ-γδ’)#i
となり、複素内積においては、複素内積(V,U)<>複素内積(U,V)、となり交換性が保たれないことが分かる。
しかし、VとUの順序を交換した複素内積(U,V)をCONJ(複素内積(V,U))と再定義すれば、複素内積(V,U) と等しくなり、交換性が、ほぼ、保たれる。また、このように見直しても、実ベクトルの内積の交換性の定義を見直す必要もありません。
すなわち、複素内積(U,V)=CONJ(複素内積(V,U))、が成り立ちます。
さて、2つの例を挙げるわね。
V≔[1+3,4+5]、U≔[5-6,10+12]、としましょう。
例1:DERIVEの内積演算は、複素内積の定義に従っていることを示す。
V・V=[1+3,4+5]・[1+3,4+5]=51、
これは、第2項の[1+3,4+5]の共役複素数が取られないとして計算した値(-17+46#i)とは、異なり、複素ベクトルの複素内積の演算規則に則ったものになっていることが分かりました。
例2:複素内積の交換性を示す。
DERIVEでは、V・U=(87+23)、であるが、U・V=(87-23)、となります。
後者は、CONJ(87+23)=CONJ(V・U)、であることを示しています。
このことからも、DERIVEの内積演算(・)は、V・U*、と計算していることが分かる。
(ここの(・)は、実ベクトルの場合の内積計算記号と考えている)
なお、複素内積には、次の性質もあります。
複素内積(V,U*)=V・U**=V・U、
複素内積(V*,U*)=V*・U**=V*・U=U・V*=複素内積(U,V)
さらに、αを複素数とした場合、αが実数の場合のa・(αb)=α×(a・b)、を拡張する必要があるわね。
複素内積(V,αU)=V・(αU)*=V・α*×U*=α*×V・U*=CONJ(α)×複素内積(V,U)、と変形できることから、
複素内積(V,αU)=CONJ(α)×複素内積(V,U)と計算する必要があることが分かります。
目次へ戻る
①で求めた固有ベクトルV1、V2、V3をその大きさ(=ノルム)1/√3で割り(=正規化)横に並べた行列をUと書けば、
となる。
また、Uの各要素の共役複素数を持つ行列U*のさらに転置行列を作ると、
となる。
U * ' は、Uの随伴行列、または、共役転置行列とも呼ばれます。
Uの右肩に、†(ダガー=短剣の印)を付けて示すこともあります。(†は、十字架(クロス)☦ではなかったわ!)
要素の「複素共役」をとった(要素をその共役複素数で置き換えた)行列は、「共役行列」(「共役複素行列」)と呼ばれます。その記法は、ここのように右肩に*を付ける以外には、上部にバーを付ける場合も多いです。
転置も、ここでは、右肩にダッシュ、あるいは、アポストロフィーを付けて示しますが、右肩に、小さな T、または、t、を付ける、あるいは、左肩に小さな
T、または、t を付ける場合もあります。
これらの記法(ノーテーション=notation)は、テキストやWebサイトにより、異なる場合がありますので、それぞれの記法をご確認下さい。なお、複素共役と転置との実行順序は、問いません。(同一の結果となることは、明らか)
このとき、この2つの行列を利用して、(U*)’×A×Uを計算すれば、(後述のように、これは、U^-1×A×U、でもあるのだけど)
と3次巡回行列が対角化されることが分かる。
ちなみに、対角化されても、行列式の値|A|は、変わりません。U*’がUの逆行列となっているため、U^-1× A× U、を計算するのと同じだからです。
すなわち、一般に変換行列をRと書けば、|R^-1 A R|=|R^-1||A||R|=|R^-1||R||A|=1×|A|=|A|、
よって、R^-1 A Rによる変換後(必ずしも対角化されなくても)も行列式の値は、変わりません。
(|R|≠0ならば、|R^-1|=1/|R|なので、|R^-1||R|=1による。)
ここで、2つの行列の積の行列式に関する、|AB|=|A||B|、を使っています。
なお、一般のn次正方行列Aの固有値の積は、|A|に等しく、固有値の和は、トレース:tr(A)=Aの対角要素の和に等しい。これは、固有方程式の根と係数の関係を考えると分かりますね。
目次へ戻る
ユニタリ行列 U とは、要素が複素数の正則行列で、その逆行列が共役転置行列である行列のことです。
すなわち、U^-1=(U*)’。
③では、対角化の変換行列として使われています。
ユニタリ行列Uの行列式の値は|U|=|(U*)’|=1です。
これは、要素が実数の実対称行列を対角化する際に用いられる直交行列、Tにおいて、Tの逆行列は、Tの転置行列であり、
T^(-1)×実対称行列×T=T ' ×実対称行列×T、により、実対称行列が対角化される場合の拡張となっています。
なお、複素ベクトル(縦ベクトル)、X=[x1,x2,・・xn]' から作られるエルミート単位2次形式、X*' X=Σxi×xj*、において、正則一次変換、Y=P
X、を行うとき、この2次形式が、Σyi×yj*、になるとき、変換行列Pをユニタリ行列、その変換をユニタリ変換と呼びます。
これは、実ベクトルの場合の直交行列、直交変換を複素数の場合に拡張したものとなっています。
目次へ戻る
DERIVEのAPPEND関数は、DERIVEで上のように縦ベクトルV1、V2、V3を並べて行列Uを作る際、利用すると便利な関数よ。
とDERIVE上で再定義し、U=APPEND(V1’,V2’,V3’)’と計算します。(’は、転置)
ちなみに、行列の位(ランク)は、RANK(A)で計算できます。RANK関数は、多分、初お目見えだと思うわ。
一方、固有方程式、固有値、固有ベクトルを求めるDERIVEの関数は、すでに何回か登場しているけど、あらためて、下に紹介しておきます。
・ 固有方程式:CHARPOLY(A,[変数名])、変数名は、省略可能。
・ 固有値:EIGENVALUES(A)、4次までは、厳密解が得られる。
・ 固有ベクトル:EXACT_EIGENVECTOR(A,厳密な固有値)
ここで、固有値が厳密解でない場合は、APPROX_EIGENVECTOR(A,近似固有値)を利用します。APPROX_EIGENVECTOR関数は、DERIVEのファイルメニューからLinearAlgebra.mthを読み込む必要があります。
上記で固有ベクトルを求めた場合は、DERIVE上の縦ベクトル表示([1;1;1]=[[1],[1],[1]])となるので、APPEND関数の引数として、そのまま、利用できます。
目次へ戻る

以下では、3次の巡回行列の例を離れて、もう少し、一般の正方行列を考えます。
3次の複素(正方)行列をAで表すと、固有ベクトルと固有値の関係から、V1、λ1等について、AV1=λ1V1、等が成り立つ。
一方、(U*)’AU=B、ここで、Bがλ1、λ2、λ3を対角要素に持つ対角行列となるための条件として、左から、Uを掛けると、AU=UB、であるが、これは、
と変形できて、AV1=λ1V1等により、満足される。逆も同様。4次以上も同様。
対角化の一つの利点は、A^nを求める場合、後述の正則一次変換行列、既出のユニタリ行列や直交行列により、対角化できれば、対角化された行列Bのn乗は、対角要素のn乗でしかないため、元のAのn乗が容易に知れることでしょう。
すなわち、対角変換のための行列をPとしたとき、変換される行列をA、対角化された行列をBとして、
P^-1×A×P=B、から、Pを左から掛けて、さらに、右から、P^-1を掛けると、A=P×B×P^-1、が得られる。
Aのn乗は、A^n=(P×B×P^-1)(P×B×P^-1)・・(P×B×P^-1)=P×B^n×P^-1、となるため、対角要素がAの固有値^nであるB^nから、A^n=P×B^n×P^-1、と求められる。(中間のすべてのP^-1×P=I、と単位行列になることに注意)
また、後述の「フロベニウスの定理」や「ケーリー-ハミルトンの定理」において、対角行列、あるいは、対角化可能な行列について、これらの定理が、ほぼ、明らかに成り立つことが分かるご利益も大きいでしょう。
さらには、数値を要素とする大きな実対称行列に対して、局所的な直交行列を繰り返し、適用し、対角要素のみを固有値とする対角行列に変換して固有値を求める「ヤコビ法」、「LR分解法(ルーティスハウザー法)」などの数値計算法でも、さまざまな線形変換が利用されます。
なお、これらの数値計算法については、例えば、『数値計算法基礎』(田中敏幸 著:コロナ社:2006年4月初版第1刷)などをご参照ください。
目次へ戻る
エルミート(エルミット)氏は、『Charles Hermite、 1822~1901、フランスの数学者。エルミートの多項式,エルミート行列,エルミート形式などでその名を知られる。また,自然対数の底 e が超越数であることの証明は著名。数学の幅広い分野で研究をすすめ,二〇世紀の数学に多くの遺産を残す。』(大辞林4.0)
複素数を要素とする「複素行列」Eが、(E*)’=E となる場合、Eを「エルミート行列(エルミット行列)」と呼びます。
エルミート行列 Eは、E^-1=(E*)’の性質がある。
Eの行列式の値と固有値は、実数である。(従って、実対称行列の行列式や固有値も実数)
例
固有値は、EigenValues(E)=[√17+3,3-√17]、
対応する固有ベクトル(ノルムを1と正規化)したものは、
対角化するためのユニタリ行列は、(Append(V1’,V2’))’により、
ここで、(CONJ(U))’×E×Uを計算すると、
となり、確かに、対角要素は、Eの固有値であり、対角要素以外の要素は、ゼロとなる。
目次へ戻る
任意の複素(正方)行列Aは、必ずしもユニタリ行列により対角化できないことに注意する必要があります。
「Aがユニタリ行列により対角化可能」な必要十分条件は、Aが「正規行列」であることです。(『行列と行列式』107~109頁)
ここで、正規行列とは、(A*)’A=A(A*)’、の性質を持つ行列のこと。対称行列の拡張となっています。
エルミート行列及びその特別な場合の実対称行列は、正規行列です。
下図のように、3次巡回行列Aは、(A*)’×A=A×(A*)’、となるので、正規行列です。
・ 正規行列の相異なる固有ベクトルは、直交する。(正規行列より広い一部の正則行列が対角化可能でも、その固有ベクトルは、直交しないことがあります。後述の例を参照)
・ 固有方程式のk重根λとしたとき、A-λIのランクは、n-kである。(正規行列よりも広い一部の正則行列が対角化可能な場合も成立する)
※ 一般に、A'×A-A×A'=δA、と定義すると、(δA)'=-δAより、
(δA)'×δA-δA×(δA)'=ゼロ行列、となります。(2022/4/9追記)
目次へ戻る
③では、正規行列がユニタリ行列により、対角化可能なことが必要十分と説明しました。
ここで、うっかりしやすいけど、「対角化可能な行列」は、正規行列だけではない」ことね。
ユニタリ変換(または直交変換)以外の正則一次変換により対角化可能な行列もあります。
例えば、下図のような2次行列は、対角化可能ですが、その固有ベクトルが直交しない例です。
Aは、|A|=1、の正則実行列ですが、実対称行列では、ありません。(従ってエルミート行列でもない)。
また、(A*)’×A<>A×(A*)’、から、正規行列でもないのです。
このため、「ユニタリ行列による対角化は、できない」けれど、一次変換行列では、対角化できる例となります。
すなわち、Aの固有値は、[√3+2,2-√3]と2根あるので、2根に対応する正規化された「固有ベクトル」は、
正規化されているので、V・V=1、U・U=1ですが、V・U<>0となり、直交しません。
※ 2つのベクトルは、一次独立なので、新しいUを新U=(V/6)√39+(U/6)√3、と定義し直せば、
V・V=1,新U・新U=1、V・新U=0、となる正規直交系を作ることは、可能。(Schmidtの方法。『行列と行列式』106頁)
V、Uから、(Append(V’,U’))’により、一次変換行列 Pを作れば、
念のため、(P*)’×P を計算しても単位行列にならないので、Pは、ユニタリ行列ではないことが分かります。
しかし、P^-1×A×P を作ると、
このように、Aは、Pにより、対角化可能であることが分かります。
目次へ戻る
とは言いながら、「すべての正方行列が対角化可能でもない」ことにも、注意する必要がありますよ。
例えば、次の2次行列は、正規行列ではないので、ユニタリ行列による対角化はできないし、さらに、どのような一次変換行列を使っても対角化できません。
上の実行列Aは、正則行列(正方行列で、|A|≠0)ですが、下図のように正規行列ではない。
一方、前例のように固有値を求めると、2根あり、[3/2+√11/2、3/2-√11/2]、となる。
対応する正規化された「固有ベクトル」は、
なお、複素内積(V,V)=1等であるが、複素内積(V,U)<>0となり、直交しない。この点は、前例と同様。
また、これらから、(Append(V’,U’))’により「一次変換行列」類似の行列Qを作り出せば、
となるものの、(Q*)’×Qを計算しても単位行列にならない。すなわち、Qは、ユニタリ行列ではない。
また、Q^-1×A×Qを作ってみても、
となって、Aは、Qにより対角化できないことが分かります。
この例では、どのような一次変換行列による変換を施しても、対角化できないことが容易に証明できます。
目次へ戻る
次の2次行列は、対角化できません。
これは、正規行列ではないのでユニタリ行列による対角化はできない。さらには、前例のような一次変換行列でも対角化できない例です。
上の実行列Aは、正則行列(正方行列で、|A|≠0)であるが、下図のように正規行列ではない。
一方、固有方程式は、(λ+1)^2=0、λ=-1が2重根となっています。
固有ベクトルをV=[v1,v2]と書けば、
このとき、v1=v2が条件として、得られますが、一つしか独立な固有ベクトルを作れずに対角化できません。
ただし、X=[x1,x2]’、としたとき、X’ A X=x2^2-3x1^2、となり、x1x2の項がありません。
そこで、Aを拡張して、X’ B X= x2^2-3x1^2、となる、Bを求めとみると、
この場合には、B≠±2、でなければ、2根があり、一次変換行列により、対角化されることが分かります。
これを見ると、Aは、ちょうど、b=2の場合と分かります。
面白いことに、上図は、b=±2で意味を持ちませんが、b→±2の極限では、
に収束することがわかります。変換行列Pは、極限では、意味を持ちませんが、この対角化行列であれば、Y'=P X'、でYに変換後、
Y' 対角化された行列 Y=-Y1^2-Y2^2、と標準化されることが分かります。
目次へ戻る
『非対称道中双六』のマルコフ推移行列は、対角化できるけど正規行列では、ないのよ。
例えば、宿場数=1のマルコフ推移確率を表す行列は、2次行列で下図のAのようになります。
これは、推移確率 p=0またはp=2の場合のみゼロ行列、すなわち、正規行列となるけど、推移確率pは、0<p=<1、のため、正規行列となることは できません。
なお、c(宿場数+1)=7までは、これまで見てきたように、一次変換行列を利用した対角化が可能でしたが、c=8以上は、固有ベクトルを求めるのが大変なので、考え方を変えて、差分法を利用して、平均日数公式を求める方向に転換した経緯がありました。
では、正方行列の中で、一次変換行列で対角化可能な行列の条件とは何か、さらに、一次変換行列で対角化できないとき、どの程度、簡略化されるか等につきましては、ここでは、取り上げる余裕がありませんでした。『行列と行列式』等のテキストをご参照下さい。
※ 大きな行列・行列式の数値計算
要素が数値の大きい次数の行列の固有値を計算する場合、固有方程式を直接、解くのではなく、実対称行列であれば、部分的な直交変換を繰り返し適用して、対角要素以外をゼロとし、対角要素を固有値として求める「ヤコビ法」、「LR(LU)分解法」などが知られています。そのような数値計算に関するテーマを、今回、取り上げることは、ふさわしくないと考えました。大きな次数の行列・行列式の実用的な数値計算法は、専門図書をご参照ください。
目次へ戻る

2つの行列の積の行列式は、|AB|=|A||B|となります。
2次行列同士の積を考えると、
なお、Bの要素の数値は、記号と考えています。
『行列式(2)』の冒頭で挙げた7つの性質の「(5)複数の行列式の和に分解できることがある」の2次行列式の場合を適用すると、
ところが、最初の2項は、異なる列同士が同じためゼロとなり、
となることが分かります。
なお、(同じ次数の正方行列)A、Bにおいて、ABとBAが異なる場合も、その行列式は、上の定理から|AB|=|BA|となることが分かります。3次以上の場合も数学的帰納法等により、証明できます。
目次へ戻る
n次正方行列Aの行列式、|A|は、『行列式(1)』の定義で述べたように、Aのn^2個の要素から、ある特別なn個を取りだした積の和となっていましたね。n次正方行列の要素のn個の積は、重複を認めないとしても、n^2個の中からn個を取り出す組み合わせ、
n^2 C n=(n^2)!/(n!(n^2-n)!)≒n^n個もあった訳。
だけど、1からnまでの異なる数字を並べた順列の並びは、n!個しかない。このn!個の順列の内、偶順列は、プラス1、奇順列は、マイナス1の符号を付けて、積和を取るというのが行列式の定義だった。
いま、ε(p1,p2,・・pn)、を[p1,p2,・・pn]が[1,2,・・n]の偶順列では、プラス1、奇順列は、マイナス1、以外は、ゼロとなる関数とすれば、|A|=Σε(p1,p2,・・pn)×a1 p1 a2 p2 ・・an pn とも定義できます。ただし、p1・・pnは、1からnまでのすべての数字を動く。
(見通しは、良いけど、数値計算には、不向きね。何と言っても、約n^n回の計算が必要だから。)
しかし、Aの行列式をF(A)と記した時、F(AB)=F(A)F(B)、となるためには、上のε関数は、上記以外の値を取ることができないことが知られています。逆に言うと、F(AB)=F(A)×F(B)、が成立するように行列式は、定義されているとも考えられますね。
(赤字部分に錯誤があったのでお詫びして訂正します。2022/4/24)
目次へ戻る

正則行列A、(|A|≠0)の逆行列、Bは、A×B=I、Iは、単位行列、と定義されます。
この逆行列、Bは、A^-1と記されて、すでに何度も登場していますね。
例えば、2次行列の場合は、下図のとおり。
これは、
を解けば、良いことが分かります。
これを解くには、『行列式(2)』で作成したDERIVEのクラメルの公式を与えるユーザー定義関数、Fcramer_user関数を使えば、B=A^-1は、
[b11,b21]=Fcramer_user(A,[1,0])、
[b12,b22]=Fcramer_user(A,[0,1])、
と2段階で求められます。
(1番目の式では、[b11,b12]ではなく「b11,b21]が得られることに注意してください。以下同様)2022/4/4追記
※ DERIVEでは、単にA^-1を計算すれば、良い。
逆行列をクラメルの公式で直接、解くのは、手間(時間)がかかります。
後述のケーリー・ハミルトンの定理の応用により求める方法の方が容易です。
※ 『行列式(1)』で紹介したDERIVEの組み込み関数、「余因子」、COFACTOR(A,j,k)を使えば、
例えば、Cofactor(A,1,k)は、|A|を1行目で展開した係数、すなわち、Aの1行目とk列を削除した行列の行列式×(-1)^-(1+k)を与えるので、Aの行列式は、|A|=Σ(k=1~n)(Element(A,1,k)×Cofactor(A,1,k))、と展開できます。
ここで、対象となる行列が、Aのk列目を単位行列の1列目で置き換えたと考えた場合、前述の逆行列のk行目を求めていると考えられます。
すなわち、Aの逆行列、A^-1の(k,1)要素を|A|で除す前の値は、COFACTOR(A,1,k)、で与えられることが分かります。
例 3次のファンデルモンドの行列、Aについて、
Cofactor(A,1,k)、k=1~3、により、逆行列の|A|で除す前のk行、1列目が求められることが分かります。
注意すべきは、Cofactor関数の列を変化して、求められるのは、行を変化したものという点です。上の例では、Cofactor関数の引数の1行、k列を変化させて、求められるのは、1列、k行目です。(k=1~3)
なお、上では、前述の例と対応させるため、分かりやすいようにAのk列目を単位行列のj列目で置き換えた行列を■で示していますが、Cofactor関数は、Aのj行、k列を削除して行列式を計算しますので、実際にAのk列目を単位行列の1列目に置き換えた引数として与える必要は、ありません。、(2022/4/8追記)
※ 第98回『行列式(2)』で取り上げたDERIVEで連立方程式を解く2つの方法を使っても、逆行列は、求められます。
・ Row_Reduce関数を使う方法
Aをn次の正方行列として、
Row_Reduce(A,Identity_Matrix(n))を計算すると、2n×n次の行列が得られます。
左側のn×n行列が単位行列、右側のn×n次行列が逆行列となります。
例:
上の図では、左側の2×2行列が単位行列、右側の2×2次行列が逆行列となっていることが分かります。
・ Solve関数を使う方法
予め、Bを下図のように定義しておけば、
Solve(A*B=Identity_matrix(2),B)、として、、
Bの要素を次のように計算してくれます。
ただし、Row_Reduce関数と異なり、「行列」の形で出てこないので、使い勝手は、良くないでしょう。
この紫字部分は、2022/4/4追記
目次へ戻る
① では、A×A^-1=Iと定義されていますが、A^-1×A=I、でもあります。
なぜなら、仮に、C×A=I、と書けば、両辺に右からA^-1を掛けて、C×A×A^-1=A^-1、
よって、C×I=C=A^-1、
目次へ戻る
Aの逆行列の逆行列は、元の行列、Aです。
これは、A×A^-1=I、から、両辺の逆行列を考えると、
(A×A^-1)^-1=I^-1、
(A^-1)^-1×A^-1=I、
よって、(A^-1)^-1=A、となるためです。
目次へ戻る
すなわち、(A’)^-1=(A^-1)’、
なぜなら、A^-1×A=I、から、両辺の転置を作ると、A'×(A^-1)’=I、となるが、
これは、(A^-1)’が(A’)^-1、であることを示しています。
目次へ戻る
A、Bが同じ次数の正則行列であれば、(A×B)^-1=B^-1×A^-1、となります。
すなわち、逆行列の定義によれば、(A×B)^-1×(A×B)=I、が成立しますが、
これは、(A×B)^-1=B^-1×A^-1、であれば、成り立つことから分かります。
目次へ戻る
Aの逆行列の行列式、|A^-1|=1/|A|、すなわち、Aの行列式の逆数です。
なぜなら、A×A^-1=I、の両辺の行列式を取れば、2つの行列の積の性質を使って、
|A×A^-1|=|A|×|A^-1|=|I|=1、よって、|A^-1|=1/|A|。
目次へ戻る

フロベニウス(Frobenius)の定理とは、次のようなものです。
n次の正則行列をAとした時、行列Aの多項式(これは、n次行列となる)をF(A)と書いて、
F(A)=a0×A^n+a1×A^n-1+・・+an×I、とします。
ここで、a0・・anは、定数。I は、単位行列。
このとき、
Aの固有値がλ1、λ2、・・λnのとき、F(A)の固有値は、F(λk)、である、ただし、k=1~n。
F(λk)の計算では、Aをスカラー量λk、に置き換えて計算します。(単位行列は、1と見なす)
これをフロペニウス(Frobenius)の定理という。(『行列と行列式』98頁)
※ この定理により、多項式をA^2と取れば、正方行列をAとしたとき、A^2の固有値は、Aの固有値の2乗となることが分かります。
この例として、たとえば、第92回『マルコフ過程(5)(非対称型道中双六:固有方程式の一般形)』に現れる行列(特にc=宿場数+1が偶数の場合)の固有方程式が固有値λの2乗を新変数xに置き換えた式として書くことができた理由は、実にここにありました。
上は、宿場数+1=cとした際のマルコフ推移を表す行列(c次)の固有多項式の一般形、ただし、λが固有値を表す変数、
w=√(4p^2-4p+λ^2)、また、pは、0~1の値を取る確率です。
特に、c=2m、m=1~5の固有多項式の具体的な形を下に示します。
[λ^2 + p - 1, λ^4 + λ^2·(2·p^2 - p - 1) + p·(p^2 - 2·p + 1), λ^6 + λ^4·(4·p^2
- 3·p - 1) + 3·p·λ^2·(p^3 - p^2 - p + 1) + p^2·(p^3 - 3·p^2 + 3·p - 1),
λ^8 + λ^6·(6·p^2 - 5·p - 1) + 5·p·λ^4·(2·p^3 - 3·p^2 + 1) + 2·p^2·λ^2·(2·p^4
- 3·p^3 - 3·p^2 + 7·p - 3) + p^3·(p^4 - 4·p^3 + 6·p^2 - 4·p + 1), λ^10
+ λ^8·(8·p^2 - 7·p - 1) + 7·p·λ^6·(3·p^3 - 5·p^2 + p + 1) + 5·p^2·λ^4·(4·p^4
- 9·p^3 + 3·p^2 + 5·p - 3) + 5·p^3·λ^2·(p^5 - 2·p^4 - 2·p^3 + 8·p^2 - 7·p
+ 2) + p^4·(p^5 - 5·p^4 + 10·p^3 - 10·p^2 + 5·p - 1)]
確かに、λ^2の式となっています。(2022/4/10追記)
Av=λv、から、AA=A^2=λAv=λv、・・、よって、A^kv=λ^kv、
F(A)u=μu、とすれば、μは、F(A)の固有値、
(a0×A^n+a1×A^n-1+・・+an×I)u=μu、
左辺は、(a0×λ^n+a1×λ^n-1・・an×I)u=F(λ)u、
よって、μ=F(λ)、
μがこれ以外にないことは、『行列と行列式』の証明をご参照下さい。
(難しくはありませんが、ここでは、略します)
目次へ戻る
2次行列の例を挙げましょう。
右辺は、Aの多項式の例。特に深い意味はありません。
Aの固有値は、([√33/2+5/2,5/2-√33/2])、です。
一方、F(A)は、
F(A)の固有値は、
([7√33/2+45/2,45/2-7√33/2])、である。
一方、フロベニウスの定理によれば、
([7√33/2+45/2,45/2-7√33/2])となる。両者は、確かに、一致しています。
目次へ戻る
3次の巡回行列式では、
固有値は、すでに以前に求めていますが、ωを1の3乗根として、再掲すれば、
λ=a+b+c、a+bω+cω^2、a+bω^2+cω、の3つです。
一方、F(A)=A^3+A^2+A+I、(この式に特別な意味はありません)、とすれば、
となります。
この長い行列をF(A)として、固有多項式は、|F(A)-z I|、zの長い式になります。
一方、F(λ)を計算すると、
λ=a+b+c、に対して、
F(λ) =(a^3 + a^2(3b + 3c + 1) + a(3b^2 + 2b(3c + 1) + 3c^2 + 2c + 1) + b^3 + b^2(3c + 1) + b(3c^2 + 2c + 1) + c^3 + c^2 + c + 1)
λ=a+bω+cω^2に対して、
F(λ)= ((2a^3 - a^2(3b + 3c - 2) - a(3b^2 + 2b(1 - 6c) + 3c^2 + 2c - 2) + 2b^3 - b^2(3c + 1) - b(3c^2 - 4c + 1) + 2c^3 - c^2 - c + 2)/2 + √3(b - c)(3a^2 - a(3b + 3c - 2) + b(3c - 1) - c + 1)/2)
λ=a+bω^2+cω、に対して、
F(λ)= ((2a^3 - a^2(3b + 3c - 2) - a(3b^2 + 2b(1 - 6c) + 3c^2 + 2c - 2) + 2b^3 - b^2(3c + 1) - b(3c^2 - 4c + 1) + 2c^3 - c^2 - c + 2)/2 + √3(c - b)(3a^2 - a(3b + 3c - 2) + b(3c - 1) - c + 1)/2)
となり、これらのF(λ)を固有多項式|F(A)-z I|のzに代入して計算すると結果がゼロとなりました。驚きですね。
目次へ戻る

ケーリー(Cayley)-ハミルトン(Hamilton)の定理とは、Fが固有多項式であれば、F(A)がゼロ行列となることを指します。
Cayley:『Arthur Cayley( 1821~1895 )イギリスの数学者。楕円関数論,不変式論,射影幾何学,n次元空間の幾何学など広範な業績を残す。なかでも行列の理論は著名。群の抽象的な扱いにも先鞭 (せんべん)をつけたほか,四色問題も彼がその困難さを指摘して脚光を浴びた。』(大辞林4.0)
Hamilton:『William Rowan Hamilton( 1805~1865 )アイルランドの数学者・物理学者・天文学者。光学を数学的に扱う道を模索し,幾何光学の基礎理論を展開。また,光の伝播と質点の運動を一括して扱うなかで,いわゆるハミルトンの原理を与え解析力学の基礎を確立した。四元数の創始でも知られ,線型代数学やベクトル解析学の形成に貢献。』(大辞林4.0)
『量子力学でも盛んに使われる「ハミルトニアン」にその名が残る』(『人物で読む 物理法則の事典』:米沢富美子 総編集:朝倉書店:2016年4月初版第2刷)
目次へ戻る
2次行列の例を挙げましょう。
ここで、λは、固有値を表します。F(λ)=λ^2-5λ-2、
このλにAを代入して計算。ただし、2の項は、2 I、Iは、Identity_matrix(2)、すなわち、2次の単位行列と解釈する。
※ Identity_matrix(n)は、DERIVEで、n次の単位行列を与える関数。
F(λ)= λ^2 - 5λ - 2*Identity_matrix(2)
ここで、λをAに置き換えると、
となりました。
対角化された行列、あるいは、対角化可能な行列について成立することは、明らかですが、対角化できない行列についても成立する証明は、『行列と行列式』等のテキストをご参照下さい。
目次へ戻る
ケーリー-ハミルトンの定理を応用すると、逆行列を求めることができます。(DET(A)≠0のとき)
②の例では、F(A)=A^2-5A-2 I=ゼロ行列、となるが、
この式の両辺にA^-1を掛けると、A-5I-2 A^-1=ゼロ行列
よって、
A^-1=(1/2)(A-5I)-ゼロ行列=(1/2)(A-5I)、と求められるので、
一方、直接、A^-1を計算すると、
となり、一致していることが分かる。
次数の大きい場合も同様に求められる。
『科学技術者のための数学ハンドブック』(Tai L. Cho 著:鈴木增雄・香取眞理・羽田野直道・野々村禎彦 訳:朝倉書店:2002年9月30日初版)によれば、
Aの固有多項式を、F(λ)=a0λ^n+a1λ^n-1・・・an、とした場合、
ケーリー-ハミルトンの定理により、F(A)=ゼロ行列、となるので、
両辺にA^-1を掛けて、次式を得る。
A^-1=-(1/an)Σ(j=0~n-1)(aj×A^(n-1-j))、
これは、Aの固有多項式が得られれば、Aの逆行列は、I~A^(n-1)、まで計算し、多項式の係数との積の和を作ることにより求められることを示している。
目次へ戻る
固有多項式の係数を配列vcに格納する。添え字は、1~n+1までとし、vcに係数を[定数項,1次項,2次項,・・,n次項]と格納。
引数:逆行列を計算したい行列を引数として、逆行列をケーリー・ハミルトンの定理の応用により求めるため、
ユーザー定義関数を Finverse_user(引数)、と定義します。
引数:逆行列を計算したい行列をA_
関数内で使用
n_:行列の次元
f_:A_の固有多項式=Charpoly(A_,z_)、で計算
vc:f_の各項の係数を定数項から最高次までの順に1からn+1個まで収納
B_:初期値として、単位行列、Identety_matrix(n_)を与える。
v_:繰り返し処理関数、ITERATE関数を使う、
v_[k_,B_,X_]を保持、ここで、k_は、vcの添え字、B_は、単位行列から順次、Aを乗じる、
Xは、A_^-1の計算の途中段階を保存
v_の初期値は、[1,単位行列,ゼロ行列]
Iterate関数でのv_の更新値は、[v_↓1+1,v_↓2×A_,v_↓3+v_↓2×vc↓(v_↓1+1)]
繰返し回数:n_
出力は、Iterate関数↓3(=Xの値)を(-vc↓1)で割った値を出力する。
DERIVEでの、実際の関数定義は、次のとおり。
Finverse_user(A_) ≔
PROG(
n_ ≔ DIMENSION(A_),
f_ ≔ CHARPOLY(A_, z_),
vc ≔ VECTOR(LIM(1/(k_ - 1)!∂(f_, z_, k_ - 1), z_, 0), k_, 1, n_ + 1),
B_ ≔ IDENTITY_MATRIX(n_),
- (ITERATE([v_↓1 + 1, v_↓2A_, v_↓3 + v_↓2vc↓(v_↓1 + 1)], v_, [1, B_, 0B_],
n_))↓3/vc↓1
)
※ f_は、関数内部での定義関数なので、f_(z_)と記載するのは、誤りとなる。(第69回『方程式の数値解法(4)(ハレー法、DERIVEのPROGとRETURN)』を参照)
ここでは、Lim(z_→0(1/(k-1)!∂(f(z_),z_,k_-1))と表したいところをLIM(1/(k_ - 1)!∂(f_,
z_, k_ - 1), z_, 0)、と書いている。(固有多項式f_をzで繰り返し微分してz^kの係数を求めています)
※ ITERATE関数は、初期値をv_に代入することを1回と数えるとn_+1回実行される。(n_は、第4引数で指定)
※ ITERATE関数のv_の初期値の第3項、0*B_は、ゼロ行列を表す。
目次へ戻る
例1:2次行列の例
Finverse_user([1, 2; 3, 4])、
([-2, 1; 3/2, - 1/2])
正解は、
となり、一致しています。
例2:3次行列の例
Finverse_user([1, 1, 3; 4, 5, 6; 8, 9, 10])
([1/2, - 17/8, 9/8; -1, 7/4, - 3/4; 1/2, 1/8, - 1/8])
正解は、
となり、一致しています。
例3:3次の巡回行列式
Finverse_user([a, b, c; c, a, b; b, c, a])
[(a^2 - bc)/(a^3 - 3abc + b^3 + c^3), (c^2 - ab)/(a^3 - 3abc + b^3 + c^3), (b^2 - ac)/(a^3 - 3abc + b^3 + c^3); (b^2 - ac)/(a^3 - 3abc + b^3 + c^3), (a^2 - bc)/(a^3 - 3abc + b^3 + c^3), (c^2 - ab)/(a^3 - 3abc + b^3 + c^3); (c^2 - ab)/(a^3 - 3abc + b^3 + c^3), (b^2 - ac)/(a^3 - 3abc + b^3 + c^3), (a^2 - bc)/(a^3 - 3abc + b^3 + c^3)]
上では、分かりにくいので、画面コピーを下に示す。
以前に求めた正解の逆行列との差を取って、
となり一致していることが確認できました。
例4 10次行列、整数値を要素とする行列
DERIVEで、Random_Matrix(10,10,10)として作られた下の行列の逆行列を求める。
第3引数、10により、要素は、-10<要素<10の整数値。
Finverse_user(上の行列)、を計算した結果、逆行列が、0.04秒にて、求められました。
画像は、大きいので、略します。
DERIVEのA^-1との差は、差し引きすることで、
となり、一致しました。
ちなみに、DERIVEのA^-1の計算は、ほぼ、瞬時に終了しましたので、ユーザー定義関数の方が、多少、時間がかかりました。
例5 10次行列、実数値を要素とする行列
DERIVEて、Random_Matrix(10,10,1)、として作成された行列の逆行列を求める。
第3引数、1により、要素は、-1<要素<1の実数値。
この場合は、概数なので、関数定義の前に次の命令を追加しておくと良いようです。
Notation ≔ Mixed
Precision ≔ Mixed
これは、オプションから、モード設定で、式変型タブの「モード」を通常の「Exact」から「Mixed」、に変更すればよい。
このようにすると、厳密な式変形が可能な場合は、厳密に行い、概数については、近似的に計算してくれます。
こうすると、10桁の精度の範囲内で、逆行列が0.3秒程度で求められました。DERIVEの逆行列の計算よりも時間は、多少かかります。
なお、厳密な値を計算させると、約20秒程度必要となりますが、次数が大きくなると途方もない時間が必要でしょう。
※ 100次元について、実験してみると、DERIVEの組み込み関数 A^-1、では、約80秒程度で近似的な逆行列を求めることができました。しかし、Finverse_user関数では、Mixedモードでも、現実的な時間では、終了しません。大きな行列の逆行列は、元の行列を分解・計算するなどの工夫が必要となります。
例6 ファンデルモンドの行列の逆行列
5次のファンデルモンドの行列は、次のとおり。
Aの逆行列は、Finverse_user(A)より、
下表に、逆行列A^-1に|A|を掛けたBを示す。
| (x2x3x4x5(x2 - x3)(x2 - x4)(x2 - x5)(x3 - x4)(x3 - x5)(x4 - x5)) | ((x2 - x3)(x2 - x4)(x2 - x5)(x3 - x4)(x3 - x5)(x5 - x4)(x2(x3(x4 + x5) + x4x5) + x3x4x5)) | ((x2 - x3)(x2 - x4)(x2 - x5)(x3 - x4)(x3 - x5)(x4 - x5)(x2(x3 + x4 + x5) + x3(x4 + x5) + x4x5)) | ((x2 - x3)(x2 + x3 + x4 + x5)(x2 - x4)(x2 - x5)(x3 - x4)(x3 - x5)(x5 - x4)) | ((x2 - x3)(x2 - x4)(x2 - x5)(x3 - x4)(x3 - x5)(x4 - x5)) |
| (x1x3x4x5(x1 - x3)(x1 - x4)(x1 - x5)(x3 - x4)(x3 - x5)(x5 - x4)) | ((x1 - x3)(x1 - x4)(x1 - x5)(x3 - x4)(x3 - x5)(x4 - x5)(x1(x3(x4 + x5) + x4x5) + x3x4x5)) | ((x1 - x3)(x1 - x4)(x1 - x5)(x3 - x4)(x3 - x5)(x5 - x4)(x1(x3 + x4 + x5) + x3(x4 + x5) + x4x5)) | ((x1 - x3)(x1 + x3 + x4 + x5)(x1 - x4)(x1 - x5)(x3 - x4)(x3 - x5)(x4 - x5)) | ((x1 - x3)(x1 - x4)(x1 - x5)(x3 - x4)(x3 - x5)(x5 - x4)) |
| (x1x2x4x5(x1 - x2)(x1 - x4)(x1 - x5)(x2 - x4)(x2 - x5)(x4 - x5)) | ((x1 - x2)(x1 - x4)(x1 - x5)(x2 - x4)(x2 - x5)(x5 - x4)(x1(x2(x4 + x5) + x4x5) + x2x4x5)) | ((x1 - x2)(x1 - x4)(x1 - x5)(x2 - x4)(x2 - x5)(x4 - x5)(x1(x2 + x4 + x5) + x2(x4 + x5) + x4x5)) | ((x1 - x2)(x1 + x2 + x4 + x5)(x1 - x4)(x1 - x5)(x2 - x4)(x2 - x5)(x5 - x4)) | ((x1 - x2)(x1 - x4)(x1 - x5)(x2 - x4)(x2 - x5)(x4 - x5)) |
| (x1x2x3x5(x1 - x2)(x1 - x3)(x1 - x5)(x2 - x3)(x2 - x5)(x5 - x3)) | ((x1 - x2)(x1 - x3)(x1 - x5)(x2 - x3)(x2 - x5)(x3 - x5)(x1(x2(x3 + x5) + x3x5) + x2x3x5)) | ((x1 - x2)(x1 - x3)(x1 - x5)(x2 - x3)(x2 - x5)(x5 - x3)(x1(x2 + x3 + x5) + x2(x3 + x5) + x3x5)) | ((x1 - x2)(x1 + x2 + x3 + x5)(x1 - x3)(x1 - x5)(x2 - x3)(x2 - x5)(x3 - x5)) | ((x1 - x2)(x1 - x3)(x1 - x5)(x2 - x3)(x2 - x5)(x5 - x3)) |
| (x1x2x3x4(x1 - x2)(x1 - x3)(x1 - x4)(x2 - x3)(x2 - x4)(x3 - x4)) | ((x1 - x2)(x1 - x3)(x1 - x4)(x2 - x3)(x2 - x4)(x4 - x3)(x1(x2(x3 + x4) + x3x4) + x2x3x4)) | ((x1 - x2)(x1 - x3)(x1 - x4)(x2 - x3)(x2 - x4)(x3 - x4)(x1(x2 + x3 + x4) + x2(x3 + x4) + x3x4)) | ((x1 - x2)(x1 + x2 + x3 + x4)(x1 - x3)(x1 - x4)(x2 - x3)(x2 - x4)(x4 - x3)) | ((x1 - x2)(x1 - x3)(x1 - x4)(x2 - x3)(x2 - x4)(x3 - x4)) |
複雑なように見えるけど、そうでもない(基本対称式の一部が現れている等)ことが分かります。(詳細は、次回に)
目次へ戻る
作成日:2022/3/31
微細な語句等を修正:2022/4/1
4.(2)逆行列、4.(4)に追記:2022/4/4
逆行列に追記、末尾の例6を表に変更:2022/4/8
3.の(1)の⑥~⑫を(2)の①~⑦に振替他:2022/4/9
4.(3)①に追記:2022/4/10
2.(5)の図の誤りを訂正:2022/4/12
語句の誤りを訂正:2022/4/19
4(1)②の錯誤を訂正:2022/4/24
誤字を訂正:2022/5/7